Sequences and Series

A mathematical sequence is an ordered list of objects, often numbers. Sometimes the numbers in a sequence are defined in terms of a previous number in the list.

Given terms in a sequence, it is often possible to find a formula for the general term of the sequence, if the formula is a polynomial.

Sigma notation, denoted by the uppercase Greek letter sigma $\left ( \Sigma \right ),$ is used to represent summations—a series of numbers to be added together.

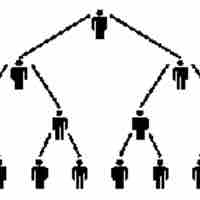
A recursive definition of a function defines its values for some inputs in terms of the values of the same function for other inputs.

An arithmetic sequence is a sequence of numbers in which the difference between the consecutive terms is constant.

An arithmetic sequence which is finite has a specific formula for its sum.

A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous one by a constant called $r$, the common ratio.

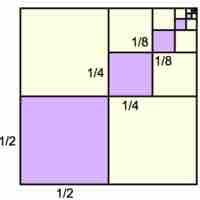
By utilizing the common ratio and the first term of a geometric sequence, we can sum its terms.

Geometric series are one of the simplest examples of infinite series with finite sums.

Geometric series have applications in math and science and are one of the simplest examples of infinite series with finite sums.

Sequences of statements are logical, ordered groups of statements that are important for mathematical induction.

Proving an infinite sequence of statements is necessary for proof by induction, a rigorous form of deductive reasoning.