Recursion

In mathematical logic and computer science, a recursive definition, or inductive definition, is used to define an object in terms of itself. A recursive definition of a function defines values of the function for some inputs in terms of the values of the same function for other inputs. 

For example, the factorial function $n!$ is defined by the rules:

$0!=1$

$(n+1)!=(n+1)n!$

This definition is valid because, for all $n$, the recursion eventually reaches the base case of $0$.

For example, we can compute $5!$ by realizing that $5!=5\cdot 4!$, and that $4!=4\cdot 3!$, and that $3!=3\cdot 2!$, and that $2!=2\cdot 1!,$ and that: 

$\displaystyle{ \begin{aligned} 1! &=1\cdot 0! \\ &= 1\cdot 1 \\ &=1 \end{aligned} }$ 

Putting this all together we get: 

$\displaystyle{ \begin{aligned} 5! &=5\cdot 4\cdot 3\cdot 2 \cdot 1 \\ &= 120 \end{aligned} }$

Recursive Formulas for Sequences

When discussing arithmetic sequences, you may have noticed that the difference between two consecutive terms in the sequence could be written in a general way:

$a_n=a_{n-1}+d$

The above equation is an example of a recursive equation since the $n$th term can only be calculated by considering the previous term in the sequence. Compare this with the equation:

$a_n=a_1+d(n-1).$

In this equation, one can directly calculate the nth-term of the arithmetic sequence without knowing the previous terms. Depending on how the sequence is being used, either the recursive definition or the non-recursive one might be more useful.

A recursive geometric sequence follows the formula: 

$a_n=r\cdot a_{n-1}$ 

An applied example of a geometric sequence involves the spread of the flu virus. Suppose each infected person will infect two more people, such that the terms follow a geometric sequence.

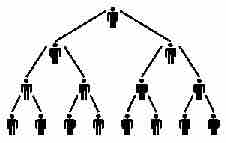
The flu virus is a geometric sequence

Each person infects two more people with the flu virus, making the number of recently-infected people the nth term in a geometric sequence.

Using this equation, the recursive equation for this geometric sequence is: 

$a_n=2 \cdot a_{n-1}$

Recursive equations are extremely powerful. One can work out every term in the series just by knowing previous terms. As can be seen from the examples above, working out and using the previous term $a_{n−1}$ can be a much simpler computation than working out $a_{n}$ from scratch using a general formula. This means that using a recursive formula when using a computer to manipulate a sequence might mean that the calculation will be finished quickly.