Geometric series played an important role in the early development of calculus, and continue as a central part of the study of the convergence of series. Geometric series are used throughout mathematics. They have important applications in physics, engineering, biology, economics, computer science, queueing theory, and finance.
Geometric series are one of the simplest examples of infinite series with finite sums, although not all of them have this property.
Repeating Decimal
A repeating decimal can be thought of as a geometric series whose common ratio is a power of
The formula for the sum of a geometric series can be used to convert the decimal to a fraction:
The formula works for any repeating term. Some more examples are:
That is, a repeating decimal with a repeating part of length
Archimedes' Quadrature of the Parabola
Archimedes used the sum of a geometric series to compute the area enclosed by a parabola and a straight line. His method was to dissect the area into an infinite number of triangles.

Archimedes' Theorem
Archimedes' dissection of a parabolic segment into infinitely many triangles.
Archimedes' Theorem states that the total area under the parabola is
The first term represents the area of the blue triangle, the second term the areas of the two green triangles, the third term the areas of the four yellow triangles, and so on. Simplifying the fractions gives:
This is a geometric series with common ratio
Fractal Geometry

Koch snowflake
The interior of a Koch snowflake is comprised of an infinite amount of triangles.
The Koch snowflake is a fractal shape with an interior comprised of an infinite amount of triangles. In the study of fractals, geometric series often arise as the perimeter, area, or volume of a self-similar figure. In the case of the Koch snowflake, its area can be described with a geometric series.
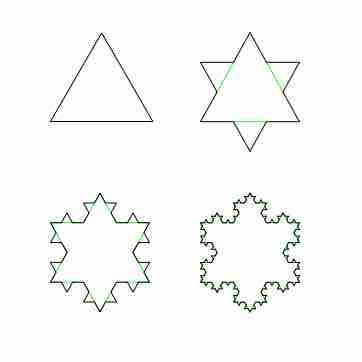
Constructing the Koch snowflake: the first four iterations
Each iteration adds a set of triangles to the outside of the shape.
The area inside the Koch snowflake can be described as the union of an infinite number of equilateral triangles. In the diagram above, the triangles added in the second iteration are exactly
The first term of this series represents the area of the first triangle, the second term the total area of the three triangles added in the second iteration, the third term the total area of the twelve triangles added in the third iteration, and so forth. Excluding the initial term
Thus the Koch snowflake has
Zeno's Paradoxes
Zeno's Paradoxes are a set of philosophical problems devised by an ancient Greek philosopher to support the doctrine that the truth is contrary to one's senses. Simply stated, one of Zeno's paradoxes says: There is a point, A, that wants to move to another point, B. If A only moves half of the distance between it and point B at a time, it will never get there, because you can continue to divide the remaining space in half forever. Zeno's mistake is in the assumption that the sum of an infinite number of finite steps cannot be finite. We now know that his paradox is not true, as evidenced by the convergence of the geometric series with