Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures.
A permutation of a set of objects is an arrangement of those objects in a particular order; the number of permutations can be counted.
The number of permutations of distinct elements can be calculated when not all elements from a given set are used.
The expression revealing the number of permutations of distinct items can be modified if not all items in a set are distinct.
A combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter.
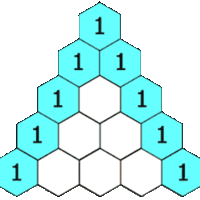
The binomial theorem, which uses Pascal's triangles to determine coefficients, describes the algebraic expansion of powers of a binomial.
The binomial theorem describes the algebraic expansion of powers of a binomial.
The rth term of any expansion can be found with the equation:
Probability is the branch of mathematics that deals with the likelihood that certain outcomes will occur. There are five basic rules, or axioms, that one must understand while studying the fundamentals of probability.
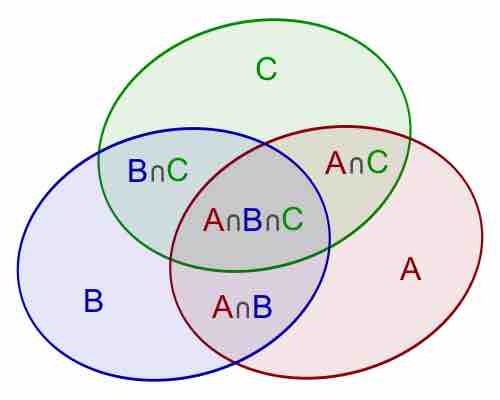
Union and intersection are two key concepts in set theory and probability.
The conditional probability of an event is the probability that an event will occur given that another event has occurred.
The complement of
The addition rule states the probability of two events is the sum of the probability that either will happen minus the probability that both will happen.
The multiplication rule states that the probability that
To say that two events are independent means that the occurrence of one does not affect the probability of the other.
The experimental probability is the ratio of the number of outcomes in which an event occurs to the total number of trials in an experiment.