Geometric series are examples of infinite series with finite sums, although not all of them have this property. Historically, geometric series played an important role in the early development of calculus, and they continue to be central in the study of the convergence of series. Geometric series are used throughout mathematics, and they have important applications in physics, engineering, biology, economics, computer science, queueing theory, and finance.

The terms of a geometric series form a geometric progression, meaning that the ratio of successive terms in the series is constant. For example, the following series:

$\displaystyle{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+ \cdots=\sum _{ n=0 }^{ \infty }{ \frac { 1 }{ { 2 }^{ n } } }}$

is geometric, because each successive term can be obtained by multiplying the previous term by $\displaystyle{\frac{1}{2}}$. 

The general form of an infinite geometric series is: 

$\displaystyle{\sum _{ n=0 }^{ \infty }{ { z }^{ n } }}$

It is possible to visualize this concept with a diagram:

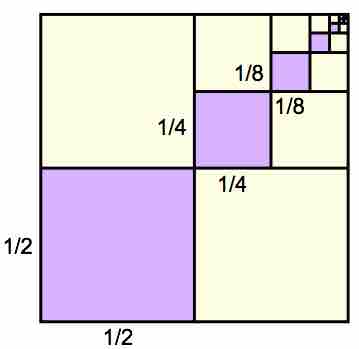
Infinite geometric series

Each of the purple squares is obtained by multiplying the area of the next larger square by $\displaystyle{\frac{1}{4}}$. The area of the first square is $\displaystyle{\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}}$, and the area of the second square is $\displaystyle{\frac{1}{4} \cdot \frac{1}{4} = \frac{1}{16}}$. 

The following are several geometric series with different common ratios. The behavior of the terms depends on the common ratio $r$:

• $4+40+400+4000+\dots$ has the common ratio $10$
• $\displaystyle{9+3+1+\frac{1}{3}+\frac{1}{9}+\dots}$ has the common ratio ${\frac{1}{3}}$
• $3+3+3+3+\dots$ has the common ratio $1$
• $\displaystyle{1-\frac{1}{2}+\frac{1}{4} -\frac{1}{8}+\dots}$ has the common ratio $-\frac{1}{2}$
• $3-3+3-3+\dots$ has the common ratio $-1$

The value of $r$ provides information about the nature of the series:

• If $r$ is between $-1$ and $+1$, the terms of the series become smaller and smaller, approaching zero in the limit, and the series converges to a sum. Consider a sequence where $r$ is one-half ${\left(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \cdots \right)}$, which has a sum of one.
• If $r$ is greater than $1$ or less than $-1$, the terms of the series become larger and larger in magnitude. The sum of the terms also gets larger and larger, and the series has no sum. The series diverges.
• If $r$ is equal to $1$, all of the terms of the series are the same. The series diverges.
• If $r$ is $-1$, the terms take two values alternately $\left(\text{e.g.}, 2,-2,2,-2,2,-2,\cdots \right)$. The sum of the terms oscillates between two values $\left(\text{e.g.}, 2,0,2,0,2,0,\cdots \right)$. This is a different type of divergence and again the series has no sum.

We can use a formula to find the sum of a finite number of terms in a sequence. For $r\neq 1$, the sum of the first $n$ terms of a geometric series is:

$\displaystyle{ \begin{aligned} s &= {a+ar+a{ r }^{ 2 }+a{ r }^{ 3 }+\cdots +a{ r }^{ n-1 } } \\ &=\sum _{ k=0 }^{ n-1 }{ a{ r }^{ k } } \\ &= a\frac { 1-{ r }^{ n } }{ 1-r } \end{aligned} }$

where $a$ is the first term of the series, and $r$ is the common ratio. 

Therefore, by utilizing the common ratio and the first term of the sequence, we can sum the first $n$ terms.

Example

Find the sum of the first five terms of the geometric sequence $\left(6, 18, 54, 162, \cdots \right)$.

In this case, $a=6$ and $n=5$. Also, note that $r = 3$, because each term is multiplied by a factor of $3$ to find the subsequent term.

Substituting these values into the sum formula, we have: 

$\displaystyle{ \begin{aligned} s &= a\frac { 1-{ r }^{ n } }{ 1-r } \\ &= 6\cdot\frac { 1-{ 3 }^{ 5 } }{ 1-3 } \\ &= 6\cdot\frac {{ -242 } }{ -2 } \\ &= 6 \cdot 121 \\ &= 726 \end{aligned} }$