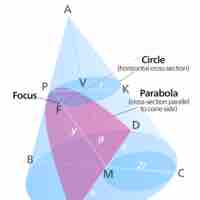
Conic sections are obtained by the intersection of the surface of a cone with a plane, and have certain features.
Every conic section has a constant eccentricity that provides information about its shape.
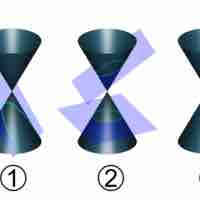
Conic sections are formed by the intersection of a plane with a cone, and their properties depend on how this intersection occurs.
The equation for a circle is an extension of the distance formula.
Understand the equation of an ellipse as a stretched circle.
Ellipses are one of the types of conic sections. The specific features of an ellipse can be determined from its equation.
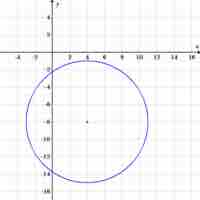
Circles and ellipses are encountered in everyday life, and knowing how to solve their equations is useful in many situations.
Hyperbolas are one of the four conic sections, and are described by certain kinds of equations.
The features of a hyperbola can be determined from its equation.
A hyperbola is an open curve with two branches and a cut through both halves of a double cone, which is not necessarily parallel to the cone's axis.
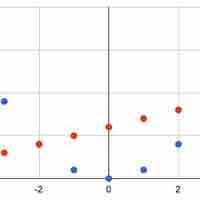
As with linear systems, a nonlinear system of equations (and conics) can be solved graphically and algebraically for all of its variables.
Nonlinear systems of equations can be used to solve complex problems involving multiple known relationships.
Systems of nonlinear inequalities can be solved by graphing boundary lines.