Chapter 8
Exponents, Logarithms, and Inverse Functions
By Boundless
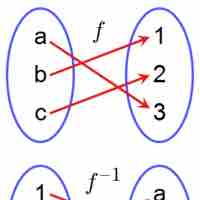
To find the inverse function, switch the
Functional composition allows for the application of one function to another; this step can be undone by using functional decomposition.

Domain restriction is important for inverse functions of exponents and logarithms because sometimes we need to find an unique inverse.

A composite function represents, in one function, the results of an entire chain of dependent functions.
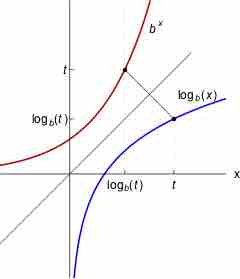
Logarithmic functions and exponential functions are inverses of each other. That is, they undo each other.
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number.

Any positive number can be used as the base of a logarithm but certain bases (
Logarithmic and exponential forms are closely related, and an equation in either form can be freely converted into the other.
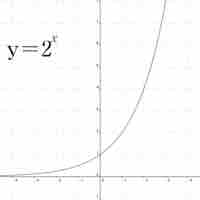
The exponential function
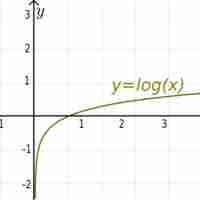
Logarithmic functions can be graphed manually or electronically with points generally determined via a calculator or table.
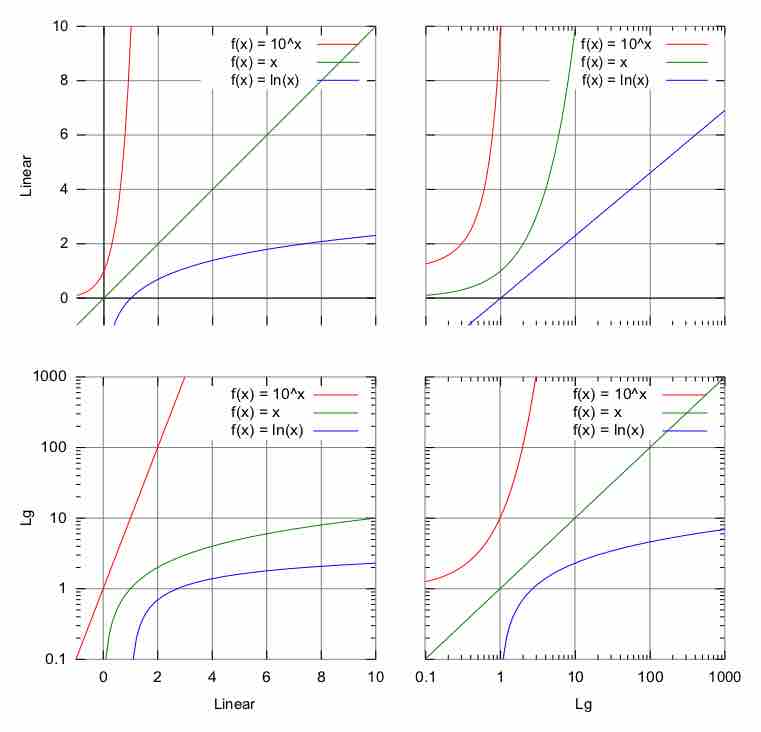
Some functions with rapidly changing shape are best plotted on a scale that increases exponentially, such as a logarithmic graph.
A useful property of logarithms states that the logarithm of a product of two quantities is the sum of the logarithms of the two factors. In symbols,
A simplifying principle of logarithms is that the logarithm of the
The logarithm of the ratio of two quantities is the difference of the logarithms of the quantities. In symbols,
A logarithm written in one base can be converted to an equal quantity written in a different base.
The number
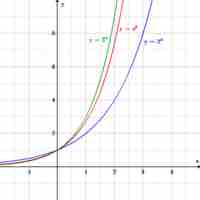
The function

The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828.

Population can fluctuate positively or negatively and can be modeled using an exponential function.
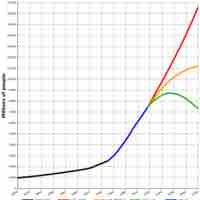
A realistic model of exponential growth must dampen when approaching a certain value. This limited growth is modelled with the logistic growth model:
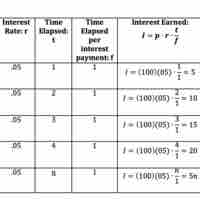
Compound interest is accrued when interest is earned not only on principal, but on previously accrued interest: it is interest on interest.
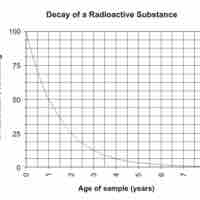
Exponential decay is the result of a function that decreases in proportion to its current value.