Introduction
Fundamentally, compound interest is an application of exponential functions that is found very commonly in every day life. Interest is, generally, a fee charged for the borrowing of money. The two classic cases are (1) interest accrued as part of loan and (2) interest accrued in a savings or other account. In the first case the client owes the amount borrowed plus the interest. In the second, the bank pays the client interest for maintaining money in the account. If you are the client, you are losing money in the first case and earning money in the second.
The amount of interest accrued depends on the principal (amount borrowed/deposited), the interest rate (a percentage of the principal), period (amount of time between interest payments) and time elapsed.
For questions of interest, unless otherwise stated, the amount borrowed/deposited remains unchanged. The client does not, for example, add or withdraw funds from the savings account after the initial deposit (the principal) is made.
Simple vs. Compound Interest
There exist two kinds of interest: simple and compound.
In simple interest, interest is accrued on the principal alone. This means that the amount of interest earned in each compounding period is the same because interest is earned based on the principal which remains unchanged.
In compound interest, interest is accrued on both the principal and on prior interest earned. For this reason, if all other conditions are the same (principal, rate, time elapsed and frequency of interest payments) compound interest grows at a faster rate than simple interest. The amount of interest earned increases with each compounding period.
Simple Interest: An Example
Simple interest is accrued linearly based on the formula:
Where
Example 1: You deposit $100 into a bank account earning 5% annual interest. How much money is in the account at the end of 1, 2, 3, 4, and $n$ years?
Let us begin by determining the interest at the end of the first year. We use the formula
The amount in the account at the conclusion of the year is given by
The table below shows the calculations, interest earned and total amount in the account after 1, 2, 3, 4, and n years.
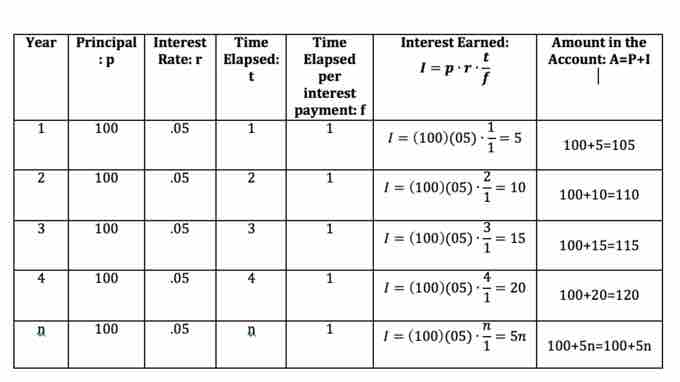
Calculations of interest earned and amount in the account for Example 1
Compound Interest: An Example
Compound interest is not linear, but exponential in form. That is, the amount of interest earned is not constant but instead changes with time based on the total amount of the amount in the account.
The equation representing investment value as a function of principal, interest rate, period and time is:
Where
We now re-consider Example 1 above. This time we use compound interest instead.
Example
2: You deposit $100 into a bank account earning 5% interest compounded annually. How
much money is in the account at the end of 1, 2, 3, 4, and $n$ years?
Let us begin by determining the amount in the account after the first year using the formula
This is the exact amount that was in the account after the first year using simple interest. That is because the difference is that compound interest earns interest on both the principal and prior interest. At the end of the first year there was no prior interest in the account. We will see differences between simple and compound interest in this, and similar problems, in the second year.
Let us determine the amount in the account after the second year again using the formula
That is, there are
The following table includes the calculations, interest earned and total amount in the account at the end of
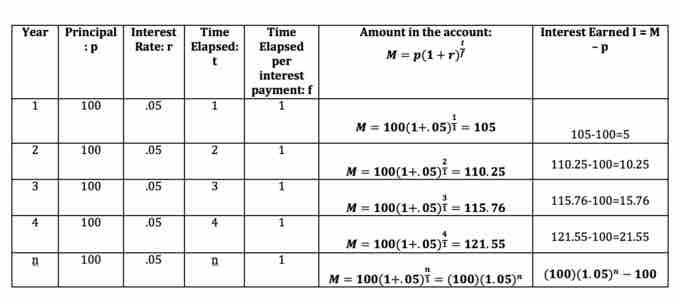
Calculations of interest earned and amount in the account for Example 2
The amount in the account is greater each year beginning with year two when using compound interest rather than simple interest. However, because the principal is so small and the number of years elapsed only 4, it does not appear that the difference between the two example is that great. Let us consider one last problem where we let the time elapsed be much greater.
Simple vs. Compound Interest Over Time: An Example
The biggest differences between the amount of money in an account using simple versus compound interest are seen over extended periods of time. To highlight this, we return the the examples we did prior and now consider how much money is in each account after 50 years.
Example 3: You deposit $100 into a bank account earning 5% interest compounded annually. How much money is in the account at the end of 50 years? How does this compare to the amount in the account after 50 years if the interest had been compounded annually?
The money in the account using simple interest after
However, the amount in the account using compound interest after
A difference of $
Frequency of Compounding Periods
The more frequent the compounding periods the more interest is accrued. Therefore, if one deposits money into a bank account that earns compound interest, and does not add or withdraw any additional funds, the amount of money in the bank would increase as the number of compounding periods per year increases. You earn more interest when interest is compounded quarterly (
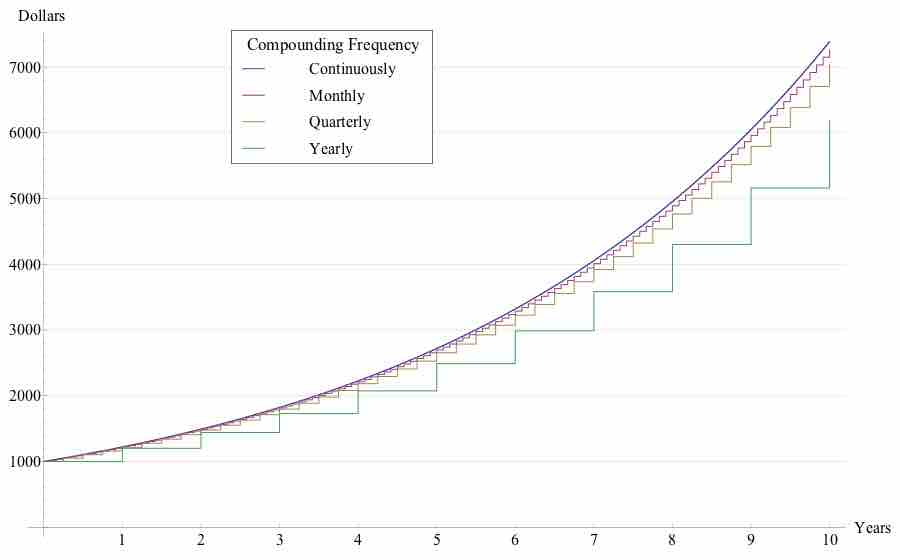
Graph of interest accrued under differing number of compounding periods per year
Starting with a principal of $1000, interest rises exponentially. The graph shows that the more frequent the number of compounding periods the more interest is accrued and shows this visually for yearly, quarterly, monthly and continuous compounding.
Interest Compounded Continuously
Given that the more frequent the compounding periods per year, the more interest is accrued it might come as a surprise that money deposited into a bank account accrues compound interest continuously. You might expect the bank would choose a smaller number of compounding periods in order to pay out less in interest, but this is not the case. To see why let us take the following example: You deposit $
The following table shows the amount in the account at the end of one year when interest is compounded with differing frequencies.

Amount in account after 1 year with interest compounded at different frequencies
What we see from the table is that while the interest earned increases as the number of compounding periods increase, that the rate at which it increases is slowing down. Going from
The formula for compound interest with the number of compounding periods going to infinity yields the formula for compounding continuously. It should come as no surprise that this formula involves the number
The formula for the amount of money in an account where interest is compounded continuously is given by