Below is the graph of the
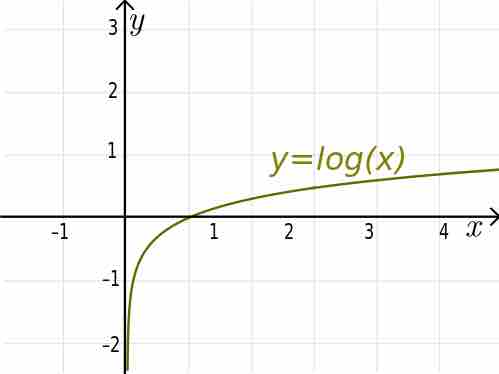
$y=\log x$
The graph of the base-
The logarithmic graph begins with a steep climb after
Properties of the Graphs of Logarithmic Functions
Special Points
The graph crosses the
Thus, we are looking for an exponent
Asymptotes
The
Let us consider what happens as the value of
Let us assume that
Thus, we are looking for an exponent such that
If we take values of
As can be seen the closer the value of
Domain and Range
The domain of the function is all positive numbers. That means that the
If the
Here we are looking for an exponent such that
The range of the function is all real numbers. That is, the graph can take on any real number.
Comparing $y=log{_x}$ and $y=\sqrt{x}$
At first glance, the graph of the logarithmic function can easily be mistaken for that of the square root function.
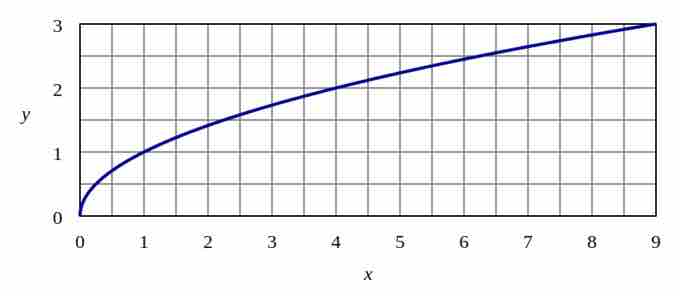
Graph of $y=\sqrt{x}$
The graph of the square root function resembles the graph of the logarithmic function, but does not have a vertical asymptote.
Both the square root and logarithmic functions have a domain limited to
Graphing Logarithmic Functions
Graphing logarithmic functions can be done by locating points on the curve either manually or with a calculator.
When graphing without a calculator, we use the fact that the inverse of a logarithmic function is an exponential function.
When graphing with a calculator, we use the fact that the calculator can compute only common logarithms (base is
Graphing Logarithmic Functions Using Their Inverses
Logarithmic functions can be graphed by hand without the use of a calculator if we use the fact that they are inverses of exponential functions.
Let us again consider the graph of the following function:
This can be written in exponential form as:
Now let us consider the inverse of this function. To do so, we interchange
The exponential function
Now we must note that these points are not on the original function (
These are:
We plot and connect these points to obtain the graph of the function
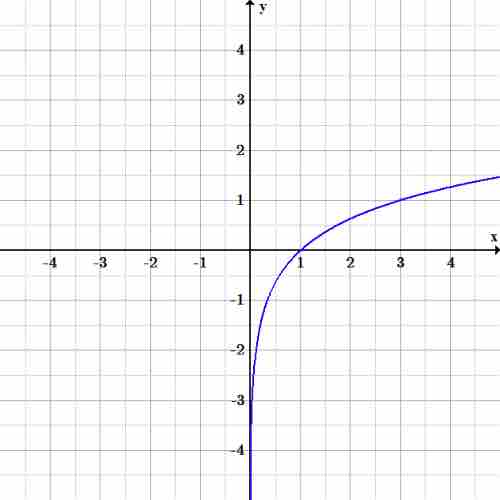
Graph of $y=log{_3}x$
The graph of the logarithmic function with base
Graphing Logarithmic Functions With Bases Between $0$ and $1$
Thus far we have graphed logarithmic functions whose bases are greater than
In fact if
Here is an example for
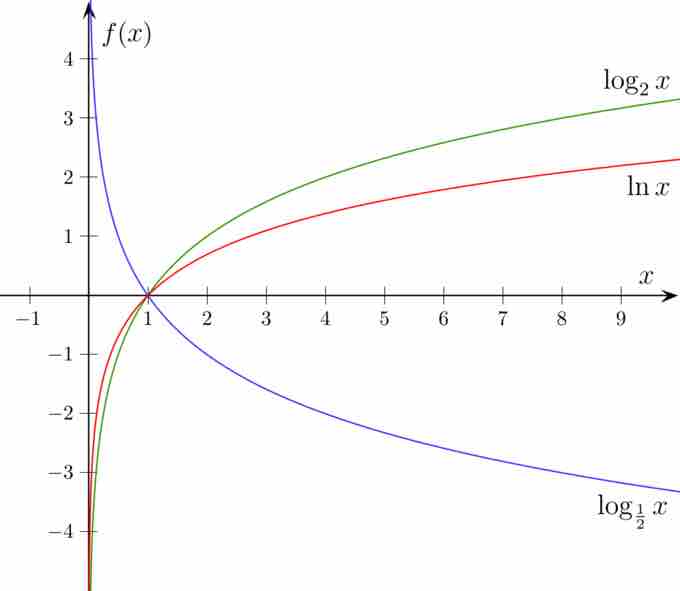
Graphs of $log{_2}x$ and $log{_\frac{1}{2}}x$
The graphs of