Definition of Inverse Function
An inverse function, which is notated
Below is a mapping of function
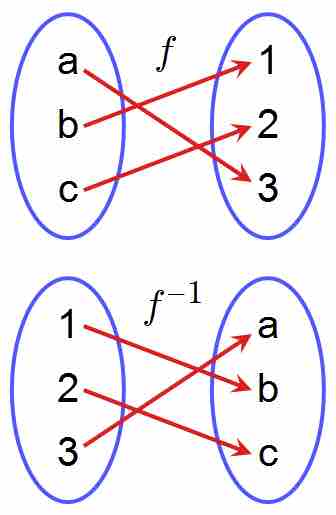
Inverse functions: mapping representation
An inverse function reverses the inputs and outputs.
Thus the graph of
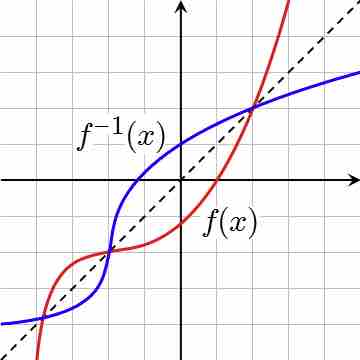
Inverse functions: graphic representation
The function graph (red) and its inverse function graph (blue) are reflected about the line
Write the Inverse Function
In general, given a function, how do you find its inverse function? Remember that an inverse function reverses the inputs and outputs. So to find the inverse function, switch the
Example 1
Find the inverse of :
a. : Write the function as:
b. : Switch the
c. : Solve for
Since the function
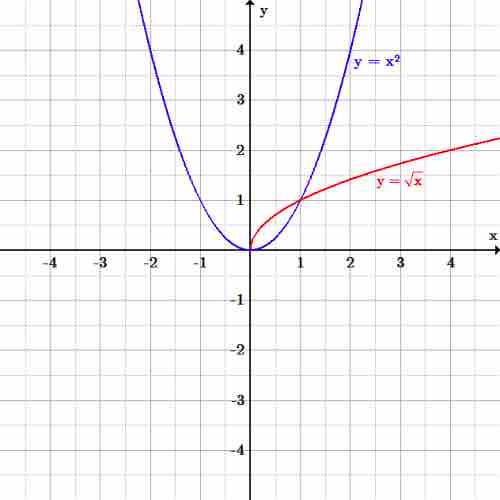
The inverse is not a function
A function's inverse may not always be a function. The function (blue)
Example 2
Find the inverse function of :
As soon as the problem includes an exponential function, we know that the logarithm reverses exponentiation. The complex logarithm is the inverse function of the exponential function applied to complex numbers. Let's see what happens when we switch the input and output values and solve for
a. : Write the function as:
b. : Switch the
c. : Solve for
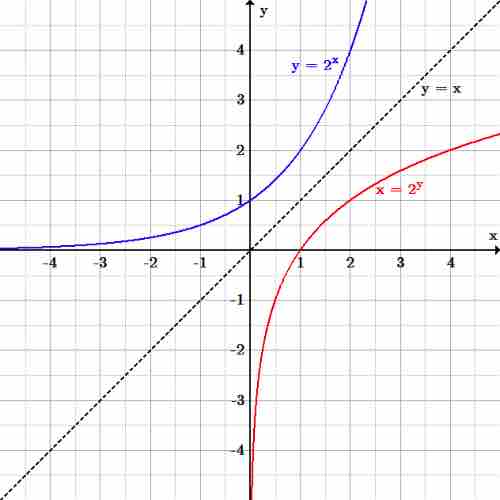
Exponential and logarithm functions
The graphs of
Test to make sure this solution fills the definition of an inverse function.
- Pick a number, and plug it into the original function.
$2\rightarrow f(x)\rightarrow 4$ . - See if the inverse function reverses this process.
$4\rightarrow f^{-1}(x)\rightarrow 2$ . ✓