The Natural Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. The natural logarithm is the logarithm with base equal to e.
The natural logarithm can be written as
Just as the exponential function with base
Graphing $y=\ln(x)$
The function slowly grows to positive infinity as
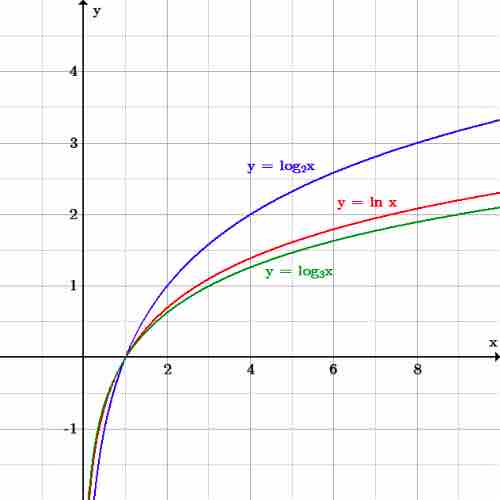
The graphs of $\log_2 x$ , $\ln x$ , and $\log_3 x$
The graph of the natural logarithm lies between the base 2 and the base 3 logarithms.
Solving Equations Using $\ln(x)$
The natural logarithm function can be used to solve equations in which the variable is in an exponent.
Example: Find the positive root of the equation $3^{x^2-1}=8$
The first step is to take the natural logarithm of both sides:
Using the power rule of logarithms it can then be written as:
Dividing both sides by
Thus the positive solution is