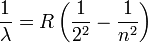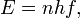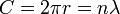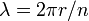Introduction to quantum mechanics
Did you know...
SOS Children volunteers helped choose articles and made other curriculum material Before you decide about sponsoring a child, why not learn about different sponsorship charities first?
| Quantum mechanics |
|---|
 Wave–particle duality
|
| Introduction Glossary · History |
|
Background
|
|
Fundamental concepts
|
|
Experiments
|
|
Formulations
|
|
Equations
|
|
Interpretations
|
|
Advanced topics
|
|
Scientists
|
Quantum mechanics (QM, or quantum theory) is a physical science dealing with the behaviour of matter and energy on the scale of atoms and subatomic particles / waves. QM also forms the basis for the contemporary understanding of how very large objects such as stars and galaxies, and cosmological events such as the Big Bang, can be analyzed and explained. Quantum mechanics is the foundation of several related disciplines including nanotechnology, condensed matter physics, quantum chemistry, structural biology, particle physics, and electronics.
The term "quantum mechanics" was first coined by Max Born in 1924. The acceptance by the general physics community of quantum mechanics is due to its accurate prediction of the physical behaviour of systems, including systems where Newtonian mechanics fails. Even general relativity is limited—in ways quantum mechanics is not—for describing systems at the atomic scale or smaller, at very low or very high energies, or at the lowest temperatures. Through a century of experimentation and applied science, quantum mechanical theory has proven to be very successful and practical.
Overview
The foundations of quantum mechanics date from the early 1800s, but the real beginnings of QM date from the work of Max Planck in 1900. Albert Einstein and Niels Bohr soon made important contributions to what is now called the "old quantum theory." However, it was not until 1924 that a more complete picture emerged with Louis de Broglie's matter-wave hypothesis and the true importance of quantum mechanics became clear. Some of the most prominent scientists to subsequently contribute in the mid-1920s to what is now called the "new quantum mechanics" or "new physics" were Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, and Erwin Schrödinger. Later, the field was further expanded with work by Julian Schwinger, Sin-Itiro Tomonaga and Richard Feynman for the development of Quantum Electrodynamics in 1947 and by Murray Gell-Mann in particular for the development of Quantum chromodynamics.

Early researchers differed in their explanations of the fundamental nature of what we now call electromagnetic radiation. Some maintained that light and other frequencies of electromagnetic radiation are composed of particles, while others asserted that electromagnetic radiation is a wave phenomenon. In classical physics these ideas are mutually contradictory. Ever since the early days of QM scientists have acknowledged that neither idea by itself can explain electromagnetic radiation.
In 1690, Christian Huygens explained the laws of reflection and refraction on the basis of a wave theory. Sir Isaac Newton believed that light consisted of infinitesimally small particles which he designated "corpuscles". In 1827 Thomas Young and Augustin Fresnel made experiments on interference that showed that a corpuscular theory of light was inadequate. Then in 1873 James Clerk Maxwell showed that by making an electrical circuit oscillate it should be possible to produce electromagnetic waves. His theory made it possible to compute the speed of electromagnetic radiation purely on the basis of electrical and magnetic measurements, and the computed value corresponded very closely to the empirically measured speed of light. In 1888, Heinrich Hertz made an electrical device that actually produced what we would now call microwaves — essentially radiation at a lower frequency than visible light. Everything up to that point suggested that Newton had been entirely wrong to regard light as corpuscular.
Later experiments indicated that a packet or quantum model was needed to explain some phenomena. When light strikes an electrical conductor it causes electrons to move away from their original positions. The observed phenomenon could only be explained by assuming that the light delivers energy in definite packets. In a photoelectric device such as the light meter in a camera, light hitting the metallic detector causes electrons to move. Greater intensities of light at one frequency can cause more electrons to move, but they will not move faster. In contrast, higher frequencies of light can cause electrons to move faster. Ergo, intensity of light controls current, but frequency of light controls voltage. These observations raised a contradiction when compared with sound waves and ocean waves, where only intensity was needed to predict the energy of the wave. In the case of light, frequency appeared to predict energy. Something was needed to explain this phenomenon and to reconcile experiments that had shown light to have particle nature with experiments that had shown it to have wave nature.
Despite the success of quantum mechanics, it does have some controversial elements. For example, the behaviour of microscopic objects described in quantum mechanics is very different from our everyday experience, which may provoke some degree of incredulity. Most of classical physics is now recognized to be composed of special cases of quantum physics theory and/or relativity theory. Dirac brought relativity theory to bear on quantum physics so that it could properly deal with events that occur at a substantial fraction of the speed of light. Classical physics, however, also deals with mass attraction (gravity), and no one has yet been able to bring gravity into a unified theory with the relativized quantum theory.
Spectroscopy and onward
It is fairly easy to see a spectrum produced by white light when it passes through a prism, the bevelled edge of a mirror or a tapered pane of glass, or through drops of rain to form a rainbow. When samples which are composed purely of one single chemical element e.g. hydrogen, are caused to emit light they may emit light at several characteristic frequencies. The frequency profile produced is characteristic of that element. Instead of there being a wide band filled with colours from violet to red, there will be isolated bands of single colours separated by darkness. Such a display is called a line spectrum. Some lines go beyond the visible frequencies and can only be detected by special photographic film or other such devices. Scientists hypothesized that an atom could radiate light the way the string on a fine violin radiates sound – not only with a fundamental frequency (in which the entire string moves the same way at once) but with several higher harmonics (formed when the string divides itself into halves and other divisions that vibrate in coordination with each other as when one half of the string is going one way as the other half of the string is going the opposite way). For a long time nobody could find a mathematical way to relate the frequencies of the line spectrum of any element.
In 1885, Johann Jakob Balmer (1825-1898) figured out how the frequencies of atomic hydrogen are related to each other. The formula is a simple one:
where 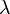 is wavelength, R is the Rydberg constant and n is an integer (n =3, 4,...) This formula can be generalized to apply to atoms that are more complicated than hydrogen, but we will stay with hydrogen for this general exposition. (That is the reason that the denominator in the first fraction is expressed as a square.)
is wavelength, R is the Rydberg constant and n is an integer (n =3, 4,...) This formula can be generalized to apply to atoms that are more complicated than hydrogen, but we will stay with hydrogen for this general exposition. (That is the reason that the denominator in the first fraction is expressed as a square.)
The next development was the discovery of the Zeeman effect, named after Pieter Zeeman (1865-1943). The physical explanation of the Zeeman effect was worked out by Hendrik Antoon Lorentz (1853-1928). Lorentz hypothesized that the light emitted by hydrogen was produced by vibrating electrons. It was possible to get feedback on what goes on within the atom because moving electrons create a magnetic field and so can be influenced by the imposition of an external magnetic field in a manner analogous to the way that one iron magnet will attract or repel another magnet.
The Zeeman effect could be interpreted to mean that light waves are originated by electrons vibrating in their orbits, but classical physics could not explain why electrons should not fall out of their orbits and into the nucleus of their atoms, nor could classical physics explain why their orbits would be such as to produce the series of discrete frequencies derived by Balmer’s formula and displayed in the line spectra. Why did the electrons not produce a continuous spectrum?
Old quantum theory
Quantum mechanics developed from the study of electromagnetic waves through spectroscopy which includes visible light seen in the colours of the rainbow, but also other waves including the more energetic waves like ultraviolet light, x-rays, and gamma rays and the waves with longer wavelengths including infrared waves, microwaves and radio waves. Only waves that travel at the speed of light are included in this description. Also, when the word "particle" is used below, it always refers to elementary or subatomic particles.
Planck's constant
Classical physics predicted that a black-body radiator would produce infinite energy, but that result was not observed in the laboratory. If black-body radiation was dispersed into a spectrum, then the amount of energy radiated at various frequencies rose from zero at one end, peaked at a frequency related to the temperature of the radiating object, and then fell back to zero. In 1900, Max Planck developed an empirical equation that could account for the observed energy curves, but he could not harmonize it with classical theory. He concluded that the classical laws of physics do not apply on the atomic scale as had earlier been assumed.
In this theoretical account, Planck allowed all possible frequencies, all possible wavelengths. However, he restricted the energy that is delivered. "In classical physics,... the energy of a given oscillator depends merely on its amplitude, and this amplitude is subject to no restriction." But, according to Planck's theory, the energy emitted by an oscillator is strictly proportional to its frequency. The higher the frequency, the greater the energy. To reach this theoretical conclusion, he postulated that a radiating body consisted of an enormous number of elementary oscillators, some vibrating at one frequency and some at another, with all frequencies from zero to infinity being represented. The energy E of any one oscillator was not permitted to take on any arbitrary value, but was proportional to some integral multiple of the frequency f of the oscillator. That is,
where n =1, 2, 3,... The proportionality constant h is called Planck's constant.
One of the most direct applications is finding the energy of photons. If h is known, and the frequency of the photon is known, then the energy of the photons can be calculated. For instance, if a beam of light illuminated a target, and its frequency was 540 × 1012 hertz, then the energy of each photon would be h × 540 × 1012 joules. The value of h itself is exceedingly small, about 6.6260693 × 10-34 joule seconds. This means that the photons in the beam of light have an energy of about 3.58 × 10-19 joules or (in another system of measurement) approximately 2.23 eV.
When the energy of a wave is described in this manner, it seems that the wave is carrying its energy in little packets. This discovery then seemed to remake the wave into a particle. These packets of energy carried along with the wave were called quanta by Planck. Quantum mechanics began with the discovery that energy is delivered in packets whose size is related to the frequencies of all electromagnetic waves (and to the color of visible light since in that case frequency determines colour). Be aware, however, that these descriptions in terms of packet, wave and particle import macro-world concepts into the quantum world, where they have only provisional relevance or appropriateness.
In early research on light, there were two competing ways to describe light, either as a wave propagated through empty space, or as small particles traveling in straight lines. Because Planck showed that the energy of the wave is made up of packets, the particle analogy became favored to help understand how light delivers energy in multiples of certain set values designated as quanta of energy. Nevertheless, the wave analogy is also indispensable for helping to understand other light phenomena. In 1905, Albert Einstein used Planck's constant to explain the photoelectric effect by postulating that the energy in a beam of light occurs in concentrations that he called light quanta, later on called photons. According to that account, a single photon of a given frequency delivers an invariant amount of energy. In other words, individual photons can deliver more or less energy, but only depending on their frequencies. Although the description that stemmed from Planck's research sounds like Newton's corpuscular account, Einstein's photon was still said to have a frequency, and the energy of the photon was accounted proportional to that frequency. The particle account had been compromised once again.
Both the idea of a wave and the idea of a particle are models derived from our everyday experience. We cannot see individual photons. We can only investigate their properties indirectly. We look at some phenomena, such as the rainbow of colours that we see when a thin film of oil rests on the surface of a puddle of water, and we can explain that phenomenon to ourselves by comparing light with waves. We look at other phenomena, such as the way a photoelectric meter in our camera works, and we explain it by analogy to particles colliding with the detection screen in the meter. In both cases we take concepts from our everyday experience and apply them to a world we have never seen.
Neither form of explanation, wave or particle, is entirely satisfactory. In general any model can only approximate that which it models. A model is useful only within the range of conditions where it is able to predict the real thing with accuracy. Newtonian physics is still a good predictor of many of the phenomena in our everyday life. To remind us that both "wave" and "particle" are concepts imported from our macro world to explain the world of atomic-scale phenomena, some physicists such as George Gamow have used the term "wavicle" to refer to whatever it is that is really there. In the following discussion, "wave" and "particle" may both be used depending on which aspect of quantum mechanical phenomena is under discussion.
Reduced Planck's (or Dirac's) constant
Planck's constant originally represented the energy that a light wave carries as a function of its frequency. A step in the development of this concept appeared in Bohr's work. Bohr was using a "planetary" or particle model of the electron, and could not understand why a 2π factor was essential to his experimentally derived formulae. Later, de Broglie postulated that electrons have frequencies, just as do photons, and that the frequency of an electron must conform to the conditions for a standing wave that can exist in a certain orbit. That is to say, the beginning of one cycle of a wave at some point on the circumference of a circle (since that is what an orbit is) must coincide with the end of some cycle. There can be no gap, no length along the circumference that is not participating in the vibration, and there can be no overlap of cycles. So the circumference of the orbit, C, must equal the wavelength, λ, of the electron multiplied by some positive integer (n = 1, 2, 3...). Knowing the circumference one can calculate wavelengths that fit that orbit, and knowing the radius, r, of the orbit one can calculate its circumference. To put all that in mathematical form,
and so
and the appearance of the 2π factor is seen to occur simply because it is needed to calculate possible wavelengths (and therefore possible frequencies) when the radius of an orbit is already known.
Again in 1925 when Werner Heisenberg developed his full quantum theory, calculations involving wave analysis called Fourier series were fundamental, and so the "reduced" version of Planck's constant (h/2π) became invaluable because it includes a conversion factor to facilitate calculations involving wave analysis. Finally, when this reduced Planck's constant appeared naturally in Dirac's equation it was then given an alternate designation, "Dirac's constant." Therefore, it is appropriate to begin with an explanation of what this constant is, even though the theories that made its use convenient have yet to be discussed.
As noted above, the energy of any wave is given by its frequency multiplied by Planck's constant. A wave is made up of crests and troughs. In a wave, a cycle is defined by the return from a certain position to the same position such as from the top of one crest to the next crest. A cycle actually is mathematically related to a circle, and both have 360 degrees. A degree is a unit of measure for the amount of turn needed to produce an arc of a certain length at a given distance. A sine curve is generated by a point on the circumference of a circle as that circle rotates. (See a demonstration at: Rotation Applet) There are 2π radians per cycle in a wave, which is mathematically related to the way a circle has 360° (which are equal to two π radians). (A radian is simply the angle if a distance along the circumference of the circle is measured equal to the radius of the circle, and then lines are drawn to the centre of the circle. This forms an angle equal to 1 radian.) Since one cycle is 2π radians, when h is divided by 2π the two "2 π" factors will cancel out leaving just the radian to contend with. So, dividing h by 2π describes a constant that, when multiplied by the frequency of a wave, gives the energy in joules per radian. The reduced Planck's constant is written in mathematical formulas as ħ, and is read as "h-bar".
-
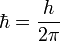 .
.
The reduced Planck's constant allows computation of the energy of a wave in units per radian instead of in units per cycle. These two constants h and ħ are merely conversion factors between energy units and frequency units. The reduced Planck's constant is used more often than h (Planck's constant) alone in quantum mechanical mathematical formulas for many reasons, one of which is that angular velocity or angular frequency is ordinarily measured in radians per second so using ħ that works in radians too will save a computation to put radians into degrees or vice-versa. Also, when equations relevant to those problems are written in terms of ħ, the frequently occurring 2π factors in numerator and denominator can cancel out, saving a computation. However, in other cases, as in the orbits of the Bohr atom, h/2π was obtained naturally for the angular momentum of the orbits. Another expression for the relation between energy and wave length is given in electron volts for energy and angstroms for wavelength: Ephoton (eV) = 12,400/λ(Å) — it appears not to involve h at all, but that is only because a different system of units has been used and now, numerically, the appropriate conversion factor is 12,400.
Bohr atom
In 1897 the particle called the electron was discovered. By means of the gold foil experiment physicists discovered that matter is, volume for volume, largely space. Once that was clear, it was hypothesized that negative charge entities called electrons surround positively charged nuclei. So at first all scientists believed that the atom must be like a miniature solar system. But that simple analogy predicted that electrons would, within about one hundredth of a microsecond, crash into the nucleus of the atom. The great question of the early 20th century was, "Why do electrons normally maintain a stable orbit around the nucleus?"
In 1913, Niels Bohr removed this substantial problem by applying the idea of discrete (non-continuous) quanta to the orbits of electrons. This account became known as the Bohr model of the atom. Bohr basically theorized that electrons can only inhabit certain orbits around the atom. These orbits could be derived by looking at the spectral lines produced by atoms.
Bohr explained the orbits that electrons can take by relating the angular momentum of electrons in each "permitted" orbit to the value of h, Planck's constant. He held that an electron in the lowest orbital has a discrete angular momentum equal to h/2π. Each orbit after the initial orbit must provide for an electron's angular momentum being an integer multiple of that lowest value. He depicted electrons in atoms as being analogous to planets in a solar orbit. However, he took Planck's constant to be a fundamental quantity that introduces special requirements at this subatomic level and that explains the spacing of those "planetary" orbits.
Bohr considered one revolution in orbit to be equivalent to one cycle in an oscillator (as in Planck's initial measurements to define the constant h) which is in turn similar to one cycle in a wave. The number of revolutions per second is (or defines) what we call the frequency of that electron or that orbital. Specifying that the frequency of each orbit must be an integer multiple of Planck's constant h would only permit certain orbits, and would also fix their size.
Bohr generalized Balmer's formula for hydrogen by replacing denominator in the term 1/4 with an explicit squared variable:
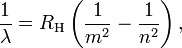 m=1,2,3,4,5,..., and n > m
m=1,2,3,4,5,..., and n > m
where λ is the wavelength of the light, RH is the Rydberg constant for hydrogen, and the integers n and m refer to the orbits between which electrons can transit. This generalization predicted many more line spectra than had been previously detected, and experimental confirmation of this prediction followed.
It follows almost immediately that if 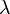 is quantized as the formula above indicates, then the momentum of any photon must be quantized. The frequency of light,
is quantized as the formula above indicates, then the momentum of any photon must be quantized. The frequency of light, 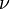 , at a given wavelength
, at a given wavelength 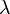 is given by the relationship
is given by the relationship
-
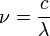 and :
and :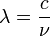 and multiplying by h/h = 1,
and multiplying by h/h = 1,
-
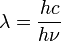 , and we know that
, and we know that
- E = hν so
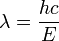 which we can rewrite as:
which we can rewrite as:
-
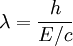 , and E/c = p (momentum) so
, and E/c = p (momentum) so
-
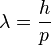 or
or 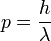
Beginning with line spectra, physicists were able to deduce empirically the rules according to which the orbits of electrons are determined and to discover something vital about the momentums involved — that they are quantized.
Bohr next realized how the angular momentum of an electron in its orbit, L, is quantized, i.e., he determined that there is some constant value K such that when it is multiplied by Planck’s constant, h, it will yield the angular momentum that pertains to the lowest orbital. When it is multiplied by successive integers it will then give the values of other possible orbitals. He later determined that K = 1/2π . (See the detailed argument at .)
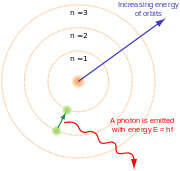
Bohr's theory represented electrons as orbiting the nucleus of an atom in a way that was amazingly different from what we see in the world of our everyday experience. He showed that when an electron changed orbits it did not move in a continuous trajectory from one orbit around the nucleus to another. Instead, it suddenly disappeared from its original orbit and reappeared in another orbit. Each distance at which an electron can orbit is a function of a quantized amount of energy. The closer to the nucleus an electron orbits, the less energy it takes to remain in that orbital. Electrons that absorb a photon gain a quantum of energy, so they jump to an orbit that is farther from the nucleus, while electrons that emit a photon lose a quantum of energy and so jump to an inner orbital. Electrons cannot gain or lose a fractional quantum of energy, and so, it is argued, they cannot have a position that is at a fractional distance between allowed orbitals. Allowed orbitals were designated as whole numbers using the letter n with the innermost orbital being designated n = 1, the next out being n = 2, and so on. Any orbital with the same value of n is called an electron shell.
Bohr's model of the atom was essentially two-dimensional because it depicts electrons as particles in circular orbits. In this context, two-dimensional means something that can be described on the surface of a plane. One-dimensional means something that can be described by a line. Because circles can be described by their radius, which is a line segment, sometimes Bohr's model of the atom is described as one-dimensional.
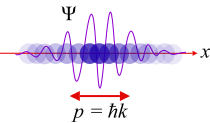
Wave-particle duality
Niels Bohr determined that it is impossible to describe light adequately by the sole use of either the wave analogy or of the particle analogy. Therefore he enunciated the principle of complementarity, which is a theory of pairs, such as the pairing of wave and particle or the pairing of position and momentum. Louis de Broglie worked out the mathematical consequences of these findings. In quantum mechanics, it was found that electromagnetic waves could react in certain experiments as though they were particles and in other experiments as though they were waves. It was also discovered that subatomic particles could sometimes be described as particles and sometimes as waves. This discovery led to the theory of wave-particle duality by Louis-Victor de Broglie in 1924, which states that subatomic entities have properties of both waves and particles at the same time.
The Bohr atom model was enlarged upon with the discovery by de Broglie that the electron has wave-like properties. In accord with de Broglie's conclusions, electrons can only appear under conditions that permit a standing wave. A standing wave can be made if a string is fixed on both ends and made to vibrate (as it would in a stringed instrument). That illustration shows that the only standing waves that can occur are those with zero amplitude at the two fixed ends. The waves created by a stringed instrument appear to oscillate in place, simply changing crest for trough in an up-and-down motion. A standing wave can only be formed when the wave's length fits the available vibrating entity. In other words, no partial fragments of wave crests or troughs are allowed. In a round vibrating medium, the wave must be a continuous formation of crests and troughs all around the circle. Each electron must be its own standing wave in its own discrete orbital.
Development of modern quantum mechanics
Full quantum mechanical theory
Werner Heisenberg made the full quantum mechanical theory in 1925 at the young age of 23. Following his mentor, Niels Bohr, Werner Heisenberg began to work out a theory for the quantum behavior of electron orbitals. Because electrons could not be observed in their orbits, Heisenberg went about creating a mathematical description of quantum mechanics built on what could be observed, that is, the light emitted from atoms in their characteristic atomic spectra. Heisenberg studied the electron orbital on the model of a charged ball on a spring, an oscillator, whose motion is anharmonic (not quite regular). For a picture of the behaviour of a charged ball on a spring see: Vibrating Charges. Heisenberg first explained this kind of observed motion in terms of the laws of classical mechanics known to apply in the macro world, and then applied quantum restrictions, discrete (non-continuous) properties, to the picture. Doing so causes gaps to appear between the predicted orbitals so that the mathematical description he formulated would then represent only the electron orbitals predicted on the basis of the atomic spectra.
In approaching the problem that Bohr gave him to solve, Heisenberg took the strategic stance that he would not deal with unobservable quantities. He would begin formulating equations using only the quantities that could be observed. That strategy led him to begin with the actual experimental evidence at hand: Measurements had been well established for such data as (1) the frequencies (and the mathematically related energies) emitted or absorbed by electron transitions from one of the Bohr stationary orbits, known to be associated with the bright line spectra, (2) the "transition amplitude" or likelihood of transition from any given orbit to any given orbit, known from the strength of the various lines in the bright spectrum, etc. From classical formulas that would characterize those phenomena Heisenberg created analogous formulas that took account of quantum conditions. Formulas that followed from the fundamental decisions made at this point resulted in good results but results that were sometimes not what one might expect. In the paper wherein he introduced quantum mechanics to the world he cautions, "A significant difficulty arises, however, if we consider two quantities x(t), y(t), and ask after their product....Whereas in classical x(t)y(t) is always equal to y(t)x(t), this is not necessarily the case in quantum theory." When the predicted values are exhibited in matrix form and multiplications are performed, the nature of the difficulty appears in a form that is more familiar to mathematicians. More significantly, empirical studies validate the theoretical results and suggest that there is something of deep importance in that the difference between x(t)y(t) and y(t)x(t) is a value related to Planck's constant.
Schema for a table of transition frequencies (produced when electrons change orbitals):
| Electron States | S1 | S2 | S3 | S4 | S5 | .... | |
|---|---|---|---|---|---|---|---|
| S1 | f1→1 | f2→1 | f3→1 | f4→1 | f5→1 | ..... | |
| S2 | f1→2 | f2→2 | f3→2 | f4→2 | f5→2 | ..... | |
| S3 | f1→3 | f2→3 | f3→3 | f4→3 | f5→3 | ..... | |
| S4 | f1→4 | f2→4 | f3→4 | f4→4 | f5→4 | ..... | |
| S5 | f1→5 | f2→5 | f3→5 | f4→5 | f5→5 | ..... | |
| S..... | ..... | ..... | ..... | ..... | ..... | ..... |
Schema for a related table showing the transition amplitudes:
| Electron States | S1 | S2 | S3 | S4 | S5 | .... | |
|---|---|---|---|---|---|---|---|
| S1 | a1→1 | a2→1 | a3→1 | a4→1 | a5→1 | ..... | |
| S2 | a1→2 | a2→2 | a3→2 | a4→2 | a5→2 | ..... | |
| S3 | a1→3 | a2→3 | a3→3 | a4→3 | a5→3 | ..... | |
| S4 | a1→4 | a2→4 | a3→4 | a4→4 | a5→4 | ..... | |
| S5 | a1→5 | a2→5 | a3→5 | a4→5 | a5→5 | ..... | |
| S..... | ..... | ..... | ..... | ..... | ..... | ..... |
As related above, Heisenberg developed ways of meaningfully relating the information in tables such as these in a mathematical way. Empirically filling in the values for tables involving quantum quantities is not a simple procedure since any measurement made on a single system gives that one value but has the potential of changing other values. So large numbers of identical copies of the system in question must be prepared, and a single measure made on each system. Multiple experiments to determine the same characteristics are made, and the results are averaged. Even then, precise measurements of all characteristics of the system as they would appear simultaneously cannot be provided because of quantum uncertainty. A precise determination of one characteristic's value necessarily creates an uncertainty in the value of its correlate. "Certain pairs of observables simply cannot be simultaneously measured to an arbitrarily high level of precision." If simultaneous measurements are made of correlated characteristics (such as position and momentum) in multiple identical systems, there will inevitably be differences in the measurements such that the difference between their products is equal to or greater than 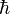 /2."
/2."
In 1925 Heisenberg published a paper entitled "Quantum-mechanical re-interpretation of kinematic and mechanical relations" relating his discoveries. So ended the old quantum theory and began the age of quantum mechanics. Heisenberg's paper gave few details that might aid readers in determining how he actually contrived to get his results for the one-dimensional models he used to form the hypothesis that proved so useful. In his paper, Heisenberg proposed to "discard all hope of observing hitherto unobservable quantities, such as the position and period of the electron", and restrict himself strictly to actually observable quantities. He needed mathematical rules for predicting the relations actually observed in nature, and the rules he produced worked differently depending on the sequence in which they were applied. "It quickly became clear that the non-commutativity (in general) of kinematical quantities in quantum theory was the really essential new technical idea in the paper."
The special type of multiplication that turned out to be required in his formula was most elegantly described by using special arrays of numbers called matrices. In ordinary situations it does not matter in which order the operations involved in multiplication are performed, but matrix multiplication does not commute. Essentially that means that it matters which order given operations are performed in. Multiplying matrix A by matrix B is not the same as multiplying matrix B by matrix A. In symbols, A×B is in general not equal to B×A. (The important thing in quantum theory is that it turned out to matter whether one experimentally measures velocity first and then immediately measures position, or vice-versa.) The matrix convention turned out to be a convenient way of organizing information and making clear the exact sequence in which calculations must be made, and it reflects in a symbolic form the unexpected results obtained in the real world.
Heisenberg approached quantum mechanics from the historical perspective that treated an electron as an oscillating charged particle. Bohr's use of this analogy had already allowed him to explain why the radii of the orbits of electrons could only take on certain values. It followed from this interpretation of the experimental results available and the quantum theory that Heisenberg subsequently created that an electron could not be at any intermediate position between two "permitted" orbits. Therefore electrons were described as "jumping" from orbit to orbit. The idea that an electron might now be in one place and an instant later be in some other place without having traveled between the two points was one of the earliest indications of the "spookiness" of quantum phenomena. Although the scale is smaller, the "jump" from orbit to orbit is as strange and unexpected as would be a case in which someone stepped out of a doorway in London onto the streets of Los Angeles. Quantum tunneling is one instance in which electrons seem to be able to move in the "spooky" way that Heisenberg ascribed to their actions within atoms.
Amplitudes of position and momentum that have a period of 2 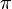 like a cycle in a wave are called Fourier series variables. Heisenberg described the particle-like properties of the electron in a wave as having position and momentum in his matrix mechanics. When these amplitudes of position and momentum are measured and multiplied together, they give intensity. However, he found that when the position and momentum were multiplied together in that respective order, and then the momentum and position were multiplied together in that respective order, there was a difference or deviation in intensity between them of h/2
like a cycle in a wave are called Fourier series variables. Heisenberg described the particle-like properties of the electron in a wave as having position and momentum in his matrix mechanics. When these amplitudes of position and momentum are measured and multiplied together, they give intensity. However, he found that when the position and momentum were multiplied together in that respective order, and then the momentum and position were multiplied together in that respective order, there was a difference or deviation in intensity between them of h/2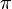 . Heisenberg would not understand the reason for this deviation until two more years had passed, but for the time being he satisfied himself with the idea that the math worked and provided an exact description of the quantum behaviour of the electron.
. Heisenberg would not understand the reason for this deviation until two more years had passed, but for the time being he satisfied himself with the idea that the math worked and provided an exact description of the quantum behaviour of the electron.
Matrix mechanics was the first complete definition of quantum mechanics, its laws, and properties that described fully the behaviour of the electron. It was later extended to apply to all subatomic particles. Very soon after matrix mechanics was introduced to the world, Schrödinger, acting independently, produced a quantum wave theory that appeared to have no similarities whatsoever to Heisenberg's theory. It was computationally easier and avoided some of the odd-sounding ideas like "quantum leaps" of an electron from one orbit to another. But within a short time Schrödinger himself had shown that the two theories produced essentially the same results in all situations. Finally, Dirac made the idea of non-commutativity central to his own theory and proved the formulations of Heisenberg and of Schrödinger to be special cases of his own theory.
Schrödinger wave equation
Because particles could be described as waves, later in 1925 Erwin Schrödinger analyzed what an electron would look like as a wave around the nucleus of the atom. Using this model, he formulated his equation for particle waves. Rather than explaining the atom by analogy to satellites in planetary orbits, he treated everything as waves whereby each electron has its own unique wavefunction. A wavefunction is described in Schrödinger's equation by three properties (later Wolfgang Pauli added a fourth). The three properties were (1) an "orbital" designation, indicating whether the particle wave is one that is closer to the nucleus with less energy or one that is farther from the nucleus with more energy, (2) the shape of the orbital, i.e., an indication that orbitals were not just spherical but other shapes, and (3) the magnetic moment of the orbital, which is a manifestation of force exerted by the charge of the electron as it rotates around the nucleus.
These three properties were called collectively the wavefunction of the electron and are said to describe the quantum state of the electron. "Quantum state" means the collective properties of the electron describing what we can say about its condition at a given time. For the electron, the quantum state is described by its wavefunction, which is designated in physics by the Greek letter 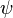 (psi, pronounced "sigh"). The three properties of Schrödinger's equation that describe the wavefunction of the electron and, therefore, also describe the quantum state of the electron as described in the previous paragraph are each called quantum numbers. The first property that describes the orbital was numbered according to Bohr's model where n is the letter used to describe the energy of each orbital. This is called the principal quantum number. The next quantum number that describes the shape of the orbital is called the azimuthal quantum number and it is represented by the letter l (lower case L). The shape is caused by the angular momentum of the orbital. The rate of change of the angular momentum of any system is equal to the resultant external torque acting on that system. In other words, angular momentum represents the resistance of a spinning object to speed up or slow down under the influence of external force. The azimuthal quantum number "l" represents the orbital angular momentum of an electron around its nucleus. However, the shape of each orbital has its own letter as well. So for the letter "l" there are other letters to describe the shapes of "l". The first shape is spherical and is described by the letter s. The next shape is like a dumbbell and is described by the letter p. The other shapes of orbitals become more complicated (see Atomic Orbitals) and are described by the letters d, f, and g. For the shape of a carbon atom, see Carbon atom. The third quantum number of Schrödinger's equation describes the magnetic moment of the electron and is designated by the letter m and sometimes as the letter m with a subscript l because the magnetic moment depends upon the second quantum number l.
(psi, pronounced "sigh"). The three properties of Schrödinger's equation that describe the wavefunction of the electron and, therefore, also describe the quantum state of the electron as described in the previous paragraph are each called quantum numbers. The first property that describes the orbital was numbered according to Bohr's model where n is the letter used to describe the energy of each orbital. This is called the principal quantum number. The next quantum number that describes the shape of the orbital is called the azimuthal quantum number and it is represented by the letter l (lower case L). The shape is caused by the angular momentum of the orbital. The rate of change of the angular momentum of any system is equal to the resultant external torque acting on that system. In other words, angular momentum represents the resistance of a spinning object to speed up or slow down under the influence of external force. The azimuthal quantum number "l" represents the orbital angular momentum of an electron around its nucleus. However, the shape of each orbital has its own letter as well. So for the letter "l" there are other letters to describe the shapes of "l". The first shape is spherical and is described by the letter s. The next shape is like a dumbbell and is described by the letter p. The other shapes of orbitals become more complicated (see Atomic Orbitals) and are described by the letters d, f, and g. For the shape of a carbon atom, see Carbon atom. The third quantum number of Schrödinger's equation describes the magnetic moment of the electron and is designated by the letter m and sometimes as the letter m with a subscript l because the magnetic moment depends upon the second quantum number l.
In May 1926 Schrödinger published a proof that Heisenberg's matrix mechanics and his own wave mechanics gave equivalent results: mathematically they were the same theory. Yet both men disagreed on the interpretation of this theory. Heisenberg saw no problem in the existence of discontinuous quantum jumps, while Schrödinger hoped that a theory based on continuous wave-like properties could avoid this "nonsense about quantum jumps" (in the words of Wilhelm Wien ).
Uncertainty principle
In 1927, Heisenberg made a new discovery on the basis of his quantum theory that had further practical consequences of this new way of looking at matter and energy on the atomic scale. In Heisenberg's matrix mechanics formula, he encountered an error or difference of h/2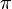 between position and momentum. The more certain the position of a particle is determined, the less certain the momentum is known, and h/2
between position and momentum. The more certain the position of a particle is determined, the less certain the momentum is known, and h/2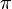 is the lower limit of the uncertainty involved. This conclusion came to be called "Heisenberg's Indeterminacy Principle", or Heisenberg's Uncertainty Principle.
is the lower limit of the uncertainty involved. This conclusion came to be called "Heisenberg's Indeterminacy Principle", or Heisenberg's Uncertainty Principle.
For moving particles in quantum mechanics, there is simply a certain degree of exactness and precision that is missing. The observer can be precise when taking a measurement of position or can be precise when taking a measurement of momentum, but there is an inverse imprecision when measuring both at the same time as in the case of a moving particle like the electron. In the most extreme case, absolute precision of one variable would entail absolute imprecision regarding the other.
Heisenberg, in a voice recording of an early lecture on the uncertainty principle pointing to a Bohr model of the atom, said:
- "You can say, well, this orbit is really not a complete orbit. Actually at every moment the electron has only an inaccurate position and an inaccurate velocity and between these two inaccuracies there is this uncertainty relation. And only by this idea it was possible to say what such an orbit was."
One consequence of the uncertainty principle was that the electron could no longer be considered as in an exact location in its orbital. Rather the electron had to be described by every point where the electron could possibly inhabit. Calculating points of probable location for the electron in its known orbital created the picture of a cloud of points in a spherical shape for the orbital of a hydrogen atom which points gradually faded out nearer to the nucleus and farther from the nucleus. This picture may be termed a probability distribution. Therefore, the Bohr atom number n for each orbital became known as an n-sphere in the three dimensional atom and was pictured as a probability cloud where the electron surrounded the atom all at once.
This led to the further description by Heisenberg that if a measurement of the electron was not being taken that it could not be described in one particular location but was everywhere in the electron cloud at once. In other words, quantum mechanics cannot give exact results, but only the probabilities for the occurrence of a variety of possible results. Heisenberg went further and said that the path of a moving particle only comes into existence once we observe it. However strange and counter-intuitive this assertion may seem, quantum mechanics does still tell us the location of the electron's orbital, its probability cloud. Heisenberg was speaking of the particle itself, not its orbital which is in a known probability distribution.
It is important to note that although Heisenberg used infinite sets of positions for the electron in his matrices, this does not mean that the electron could be anywhere in the universe. Rather there are several laws that show the electron must be in one localized probability distribution. An electron is described by its energy in Bohr's atom which was carried over to matrix mechanics. Therefore, an electron in a certain n-sphere had to be within a certain range from the nucleus depending upon its energy. This restricts its location. Also, the number of places an electron can be is also called "the number of cells in its phase space". The Uncertainty Principle set a lower limit to how finely one can chop up classical phase space, so the number of places that an electron can be in its orbital becomes finite. An electron's location in an atom is defined to be in its orbital, but stops at the nucleus and before the next n-sphere orbital begins.
Classical physics had shown since Newton that if the position of stars and planets and details about their motions were known then where they will be in the future can be predicted. For subatomic particles, Heisenberg denied this notion showing that due to the uncertainty principle one cannot know the precise position and momentum of a particle at a given instant, so its future motion cannot be determined, but only a range of possibilities for the future motion of the particle can be described.
These notions arising from the uncertainty principle only arise at the subatomic level and were a consequence of wave-particle duality. As counter-intuitive as they may seem, quantum mechanical theory with its uncertainty principle has been responsible for major improvements in the world's technology from computer components to fluorescent lights to brain scanning techniques.
Wavefunction collapse
Schrödinger's wave equation with its unique wavefunction for a single electron is also spread out in a probability distribution like Heisenberg's quantized particle-like electron. This is because a wave is naturally a widespread disturbance and not a point particle. Therefore, Schrödinger's wave equation has the same predictions made by the uncertainty principle because uncertainty of location is built into the definition of a widespread disturbance like a wave. Uncertainty only needed to be defined from Heisenberg's matrix mechanics because the treatment was from the particle-like aspects of the electron. Schrödinger's wave equation shows that the electron is in the probability cloud at all times in its probability distribution as a wave that is spread out. Max Born discovered in 1928 that when the square of Schrödinger's wavefunction (psi-squared) is computed the electron's location as a probability distribution is obtained. Therefore, to the extent that a measurement of the position of an electron can be made at an exact location instead of as a probability distribution, the electron appears to momentarily cease to have wave-like properties. Without wave-like properties, none of Schrödinger's definitions of the electron being wave-like makes sense. The measurement of the position of the particle nullifies the simple wave-like properties and the one body form of Schrödinger's equation then fails. Because the electron can no longer be described by its separate wavefunction when measured, due to its wave length becoming much shorter and its becoming entangled with the particles of the measuring apparatus, this is called wavefunction collapse.
Eigenstates and eigenvalues
The term eigenstate is derived from the German/Dutch word "eigen," which means "inherent" or "characteristic." The word eigenstate is descriptive of the measured state of some object that possesses quantifiable characteristics such as position, momentum, etc. The state being measured and described must be an " observable" (i.e. something that can be experimentally measured either directly or indirectly like position or momentum), and must have a definite value. In the everyday world, it is natural and intuitive to think of everything being in its own eigenstate. Everything appears to have a definite position, a definite momentum, a definite value of measure, and a definite time of occurrence. However, quantum mechanics affirms that it is impossible to pinpoint exact values for the momentum of a certain particle like an electron in a given location at a particular moment in time, or, alternatively, that it is impossible to give an exact location for such an object when the momentum has been measured. Due to the uncertainty principle, statements regarding both the position and momentum of particles can only be given in terms of a range of probabilities, a "probability distribution". Eliminating uncertainty in one term maximizes uncertainty in regard to the second parameter.
Therefore it became necessary to have a way to clearly formulate the difference between the state of something that is uncertain in the way just described, such as an electron in a probability cloud, and effectively contrast it to the state of something that is not uncertain, something that has a definite value. When something is in the condition of being definitely "pinned-down" in some regard, it is said to possess an eigenstate. For example, if the position of an electron has been made definite, it is said to have an eigenstate of position.
A definite value, such as the position of an electron that has been successfully located, is called the eigenvalue of the eigenstate of position. The German word "eigen" was first used in this context by the mathematician David Hilbert in 1904. Schrödinger's wave equation gives wavefunction solutions, meaning the possibilities where the electron might be, just as does Heisenberg's probability distribution. As stated above, when a wavefunction collapse occurs because something has been done to locate the position of an electron, the electron's state becomes an eigenstate of position, meaning that the position has a known value.
The Pauli exclusion principle
The Pauli Exclusion Principle states that no electron (or other fermion) can be in the same quantum state as another within an atom.
Wolfgang Pauli developed the Exclusion Principle from what he called a "two-valued quantum degree of freedom" to account for the observation of a doublet, meaning a pair of lines, in the spectrum of the hydrogen atom. The observation meant that there was more energy in the electron orbital from magnetic moment than had previously been described. In early 1925, the young physicists Uhlenbeck and Goudsmit introduced a theory that the electron rotates in space in the same way that the earth rotates on its axis. This would account for the missing magnetic moment and allow for two electrons in the same orbital to be different if their spins were in opposite directions, thus satisfying the Exclusion Principle.
According to Schrödinger's equation, there are three quantum states of the electron, but if two electrons can be in the same orbital, there has to be another quantum number (the two-valued quantum degree of freedom) to distinguish the two electrons from each other. A single electron cannot have the same four quantum numbers as another electron in the same atomic orbital. Where two electrons are in the same n-sphere and therefore share the same principal quantum number, they must then have some other unique quantum number of shape l, magnetic moment m or spin s. Where electrons are not in an orbital around the nucleus of an atom, such as in the formation of degenerate gases, they must still follow the Pauli Exclusion Principle when in a confined space.
Dirac wave equation
In 1928, Paul Dirac worked out a variation of the Schrödinger equation that accounted for a fourth property of the electron in its orbital. Paul Dirac introduced the fourth quantum number called the spin quantum number designated by the letter s to the new Dirac equation of the wavefunction of the electron. In 1930, Dirac combined Heisenberg's matrix mechanics with Schrödinger's wave mechanics into a single quantum mechanical representation in his Principles of Quantum Mechanics. The quantum picture of the electron was now complete.
All of the above development of quantum theory was based mainly on the atomic spectrum of the hydrogen atom. This is due to the fact that each atom of each element produces a unique pattern of spectral lines when light from each different kind of element is passed through a prism. Scientists could not study the electron and nucleus of the atom itself because they cannot be seen. Even today with High-resolution Scanning Tunneling Electron Microscopes we can only get images of the atom as a blurry fuzzball. However, the spectral lines of the atom reveal the orbits of electrons and the energy that can be expected. It was basically this study of the spectroscopic analysis of first the hydrogen atom and then the helium atom that led to quantum theory. Therefore, the mathematical formulas were made to fit the picture of the atomic spectrum. That is why quantum mechanics is sometimes referred to as a form of mathematical physics.
Quantum entanglement
Albert Einstein rejected Heisenberg's Uncertainty Principle insofar as it seemed to imply more than a necessary limitation on human ability to actually know what occurs in the quantum realm. In a letter to Max Born in 1926, Einstein famously declared that "God does not play dice". The bare surface level prescription for making predictions from quantum mechanics, based on Born's rule for computing probabilities, became known as the Copenhagen Interpretation of quantum mechanics. Bohr spent many years developing and refining this interpretation in light of Einstein's objections. After the 1930 Solvay conference, Einstein never again challenged the Copenhagen interpretation on technical points, but did not cease a philosophical attack on the interpretation, on the grounds of realism and locality. Einstein, in trying to show that quantum theory was not a complete theory, recognized that the theory predicted that two or more particles that have interacted in the past can exhibit strong correlations when various measurements are made on them. He wanted this to be explained in a classical way through their common past, and preferably not by a "spooky action at a distance". The argument is worked out in a famous paper devoted to what is now called the EPR paradox (Einstein-Podolsky-Rosen, 1935). Assuming what is now usually called " local realism", the EPR attempts to show from quantum theory that particles simultaneously possess both position and momentum, while according to the Copenhagen interpretation, only one of these two properties only briefly exists, in the moment that it is being measured. Einstein considered this conclusion a proof that quantum theory was incomplete since it refuses to discuss physical properties which objectively exist in nature. The feature of quantum theory leading to these paradoxes is called quantum entanglement. It means that the properties of several separate objects cannot be described by considering them separately, even after taking account of the history of their past interaction. The 1935 paper of Einstein, Podolsky and Rosen is currently Einstein's most cited publication in physics journals.
Bohr's original response to Einstein was that the particles were part of one indivisible system. Einstein's challenge led to decades of substantial research into quantum entanglement. The research would seem to confirm Bohr's objection that the two entangled particles must be viewed together as one whole, and moreover, that difficulties only arise by insisting on the reality of outcomes of measurements that are not made anyway. Moreover, God does throw dice, though rather peculiar ones. A real dice throw can be completely understood with classical mechanics, and the outcome is merely a function of the initial conditions. However the outcome of tossing quantum dice has no antecedent; no cause or explanation at all.
Interpretations
According to the correspondence principle and Ehrenfest's theorem as a system becomes larger or more massive ( action >> h ) the classical dynamics tends to emerge, with some exceptions, such as superfluidity. This is why we can usually ignore quantum mechanics when dealing with everyday objects; instead the classical description will suffice. Even so, trying to make sense of quantum theory is an ongoing process which has spawned a number of interpretations of quantum theory, ranging from the conventional Copenhagen Interpretation to hidden variables and many worlds. There seems to be no end in sight to the philosophical musings on the subject; however the empirical or technical success of the theory is unrivalled; all modern fundamental physical theories are quantum theories, relativity being subsumed within quantum field theories.