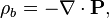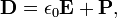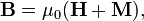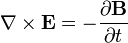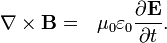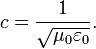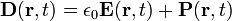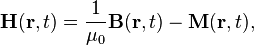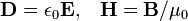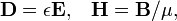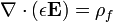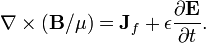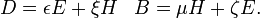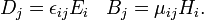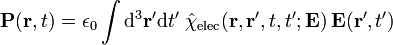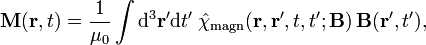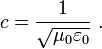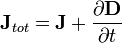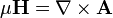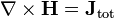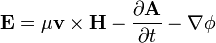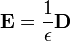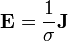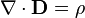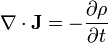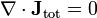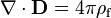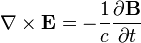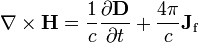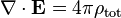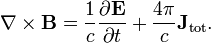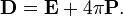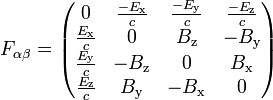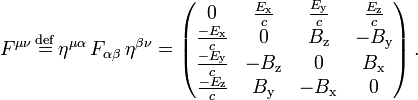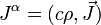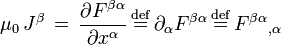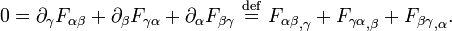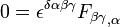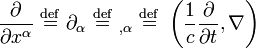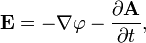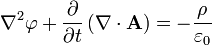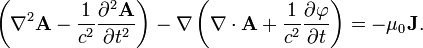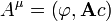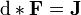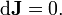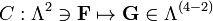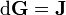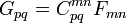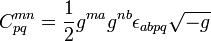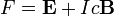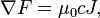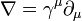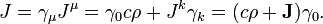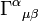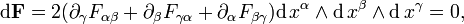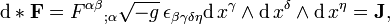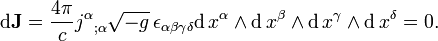Maxwell's equations
Background to the schools Wikipedia
Arranging a Wikipedia selection for schools in the developing world without internet was an initiative by SOS Children. A quick link for child sponsorship is http://www.sponsor-a-child.org.uk/
| Electromagnetism |
|---|
 |
|
Electrostatics
|
|
Magnetostatics
|
|
Electrodynamics
|
|
Electrical network
|
|
Covariant formulation
Electromagnetic tensor
( stress–energy tensor)
|
Maxwell's equations are a set of four partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These in turn underlie the present radio-, television-, phone-, and information-technologies.
Maxwell's equations have two major variants. The "microscopic" set of Maxwell's equations uses total charge and total current including the difficult-to-calculate atomic level charges and currents in materials. The "macroscopic" set of Maxwell's equations defines two new auxiliary fields that can sidestep having to know these 'atomic' sized charges and currents.
Maxwell's equations are named after the Scottish physicist and mathematician James Clerk Maxwell, since they are all found in a four-part paper, On Physical Lines of Force, which he published between 1861 and 1862. The mathematical form of the Lorentz force law also appeared in this paper.
It is often useful to write Maxwell's equations in other forms which are often called Maxwell's equations as well. A relativistic formulation in terms of covariant field tensors is used in special relativity. While, in quantum mechanics, a version based on the electric and magnetic potentials is preferred.
Conceptual description
Conceptually, Maxwell's equations describe how electric charges and electric currents act as sources for the electric and magnetic fields. Further, it describes how a time varying electric field generates a time varying magnetic field and vice versa. (See below for a mathematical description of these laws.) Of the four equations, two of them, Gauss's law and Gauss's law for magnetism, describe how the fields emanate from charges. (For the magnetic field there is no magnetic charge and therefore magnetic fields lines neither begin nor end anywhere.) The other two equations describe how the fields 'circulate' around their respective sources; the magnetic field 'circulates' around electric currents and time varying electric field in Ampère's law with Maxwell's correction, while the electric field 'circulates' around time varying magnetic fields in Faraday's law.
Gauss's law
Gauss's law describes the relationship between an electric field and the generating electric charges: The electric field points away from positive charges and towards negative charges. In the field line description, electric field lines begin only at positive electric charges and end only at negative electric charges. 'Counting' the number of field lines in a closed surface, therefore, yields the total charge enclosed by that surface. More technically, it relates the electric flux through any hypothetical closed " Gaussian surface" to the electric charge within the surface.
Gauss's law for magnetism
Gauss's law for magnetism states that there are no "magnetic charges" (also called magnetic monopoles), analogous to electric charges. Instead, the magnetic field due to materials is generated by a configuration called a dipole. Magnetic dipoles are best represented as loops of current but resemble positive and negative 'magnetic charges', inseparably bound together, having no net 'magnetic charge'. In terms of field lines, this equation states that magnetic field lines neither begin nor end but make loops or extend to infinity and back. In other words, any magnetic field line that enters a given volume must somewhere exit that volume. Equivalent technical statements are that the total magnetic flux through any Gaussian surface is zero, or that the magnetic field is a solenoidal vector field.
Faraday's law
Faraday's law describes how a time varying magnetic field creates ("induces") an electric field. This aspect of electromagnetic induction is the operating principle behind many electric generators: for example a rotating bar magnet creates a changing magnetic field, which in turn generates an electric field in a nearby wire. (Note: there are two closely related equations which are called Faraday's law. The form used in Maxwell's equations is always valid but more restrictive than that originally formulated by Michael Faraday.)
Ampère's law with Maxwell's correction
Ampère's law with Maxwell's correction states that magnetic fields can be generated in two ways: by electrical current (this was the original "Ampère's law") and by changing electric fields (this was "Maxwell's correction").
Maxwell's correction to Ampère's law is particularly important: It means that a changing magnetic field creates an electric field, and a changing electric field creates a magnetic field. Therefore, these equations allow self-sustaining "electromagnetic waves" to travel through empty space (see electromagnetic wave equation).
The speed calculated for electromagnetic waves, which could be predicted from experiments on charges and currents, exactly matches the speed of light; indeed, light is one form of electromagnetic radiation (as are X-rays, radio waves, and others). Maxwell understood the connection between electromagnetic waves and light in 1861, thereby unifying the previously-separate fields of electromagnetism and optics.
Units and summary of equations
Maxwell's equations vary with the unit system used. Though the general form remains the same, various definitions get changed and different constants appear at different places. The equations in this section are given in SI units. Other units commonly used are Gaussian units (based on the cgs system), Lorentz-Heaviside units (used mainly in particle physics) and Planck units (used in theoretical physics). See below for CGS-Gaussian units.
For a description of the difference between the microscopic and macroscopic variants of Maxwell's equations see the relevant sections below.
In the equations given below, symbols in bold represent vector quantities, and symbols in italics represent scalar quantities. The definitions of terms used in the two tables of equations are given in another table immediately following.
Table of 'microscopic' equations
| Name | Differential form | Integral form |
|---|---|---|
| Gauss's law | 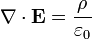 |
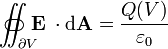 |
| Gauss's law for magnetism | 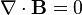 |
 |
| Maxwell–Faraday equation (Faraday's law of induction) |
 |
 |
| Ampère's circuital law (with Maxwell's correction) |
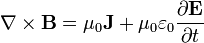 |
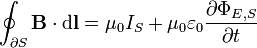 |
Table of 'macroscopic' equations
| Name | Differential form | Integral form |
|---|---|---|
| Gauss's law | 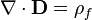 |
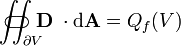 |
| Gauss's law for magnetism | 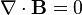 |
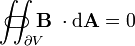 |
| Maxwell–Faraday equation ( Faraday's law of induction) |
 |
 |
| Ampère's circuital law (with Maxwell's correction) |
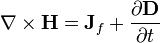 |
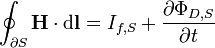 |
Table of terms used in Maxwell's equations
The following table provides the meaning of each symbol and the SI unit of measure:
| Symbol | Meaning (first term is the most common) | SI Unit of Measure |
|---|---|---|
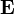 |
electric field also called the electric field intensity |
volt per meter or, equivalently, newton per coulomb |
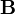 |
magnetic field also called the magnetic induction also called the magnetic field density also called the magnetic flux density |
tesla, or equivalently, weber per square meter, volt- second per square meter |
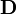 |
electric displacement field also called the electric induction also called the electric flux density |
coulombs per square meter or equivalently, newton per volt- meter |
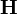 |
magnetizing field also called auxiliary magnetic field also called magnetic field intensity also called magnetic field |
ampere per meter |
 |
the divergence operator | per meter (factor contributed by applying either operator) |
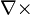 |
the curl operator | |
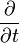 |
partial derivative with respect to time | per second (factor contributed by applying the operator) |
 |
differential vector element of surface area A, with infinitesimally small magnitude and direction normal to surface S | square meters |
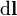 |
differential vector element of path length tangential to the path/curve | meters |
 |
permittivity of free space, also called the electric constant, a universal constant | farads per meter |
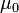 |
permeability of free space, also called the magnetic constant, a universal constant | henries per meter, or newtons per ampere squared |
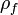 |
free charge density (not including bound charge) | coulombs per cubic meter |
 |
total charge density (including both free and bound charge) | coulombs per cubic meter |
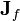 |
free current density (not including bound current) | amperes per square meter |
 |
total current density (including both free and bound current) | amperes per square meter |
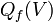 |
net free electric charge within the three-dimensional volume V (not including bound charge) | coulombs |
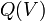 |
net electric charge within the three-dimensional volume V (including both free and bound charge) | coulombs |
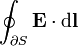 |
line integral of the electric field along the boundary ∂S of a surface S (∂S is always a closed curve). | joules per coulomb |
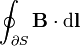 |
line integral of the magnetic field over the closed boundary ∂S of the surface S | tesla-meters |
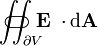 |
the electric flux ( surface integral of the electric field) through the ( closed) surface 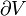 (the boundary of the volume V) (the boundary of the volume V) |
joule-meter per coulomb |
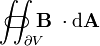 |
the magnetic flux ( surface integral of the magnetic B-field) through the ( closed) surface 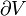 (the boundary of the volume V) (the boundary of the volume V) |
tesla meters-squared or webers |
 |
magnetic flux through any surface S, not necessarily closed | webers or equivalently, volt-seconds |
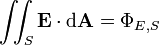 |
electric flux through any surface S, not necessarily closed | joule-meters per coulomb |
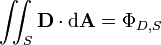 |
flux of electric displacement field through any surface S, not necessarily closed | coulombs |
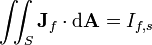 |
net free electrical current passing through the surface S (not including bound current) | amperes |
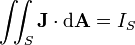 |
net electrical current passing through the surface S (including both free and bound current) | amperes |
Proof that the two general formulations are equivalent
The two alternate general formulations of Maxwell's equations given above are mathematically equivalent and related by the following relations:
where P and M are polarization and magnetization, and ρb and Jb are bound charge and current, respectively. Substituting these equations into the 'macroscopic' Maxwell's equations gives identically the microscopic equations.
Maxwell's 'microscopic' equations
The microscopic variant of Maxwell's equation expresses the electric E field and the magnetic B field in terms of the total charge and total current present including the charges and currents at the atomic level. It is sometimes called the general form of Maxwell's equations or "Maxwell's equations in a vacuum". Both variants of Maxwell's equations are equally general, though, as they are mathematically equivalent. The microscopic equations are most useful in waveguides for example, when there are no dielectric or magnetic materials nearby.
| Name | Differential form | Integral form |
|---|---|---|
| Gauss's law | 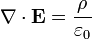 |
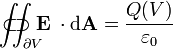 |
| Gauss's law for magnetism | 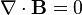 |
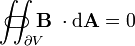 |
| Maxwell–Faraday equation (Faraday's law of induction) |
 |
 |
| Ampère's circuital law (with Maxwell's correction) |
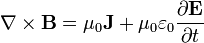 |
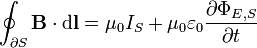 |
With neither charges nor currents
In a region with no charges (ρ = 0) and no currents (J = 0), such as in a vacuum, Maxwell's equations reduce to:
These equations lead directly to E and B satisfying the wave equation for which the solutions are linear combinations of plane waves traveling at the speed of light,
In addition, E and B are mutually perpendicular to each other and the direction of motion and are in phase with each other. A sinusoidal plane wave is one special solution of these equations.
In fact, Maxwell's equations explain how these waves can physically propagate through space. The changing magnetic field creates a changing electric field through Faraday's law. In turn, that electric field creates a changing magnetic field through Maxwell's correction to Ampère's law. This perpetual cycle allows these waves, now known as electromagnetic radiation, to move through space at velocity c.
Maxwell's 'macroscopic' equations
Unlike the 'microscopic' equations, "Maxwell's macroscopic equations", also known as Maxwell's equations in matter, factor out the bound charge and current to obtain equations that depend only on the free charges and currents. These equations are more similar to those that Maxwell himself introduced. The cost of this factorization is that additional fields need to be defined: the displacement field D which is defined in terms of the electric field E and the polarization P of the material, and the magnetic-H field, which is defined in terms of the magnetic-B field and the magnetization M of the material.
Bound charge and current
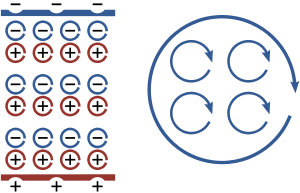
When an electric field is applied to a dielectric material its molecules respond by forming microscopic electric dipoles—their atomic nuclei move a tiny distance in the direction of the field, while their electrons move a tiny distance in the opposite direction. This produces a macroscopic bound charge in the material even though all of the charges involved are bound to individual molecules. For example, if every molecule responds the same, similar to that shown in the figure, these tiny movements of charge combine to produce a layer of positive bound charge on one side of the material and a layer of negative charge on the other side. The bound charge is most conveniently described in terms of a polarization, P, in the material. If P is uniform, a macroscopic separation of charge is produced only at the surfaces where P enter and leave the material. For non-uniform P, a charge is also produced in the bulk.
Somewhat similarly, in all materials the constituent atoms exhibit magnetic moments that are intrinsically linked to the angular momentum of the atoms' components, most notably their electrons. The connection to angular momentum suggests the picture of an assembly of microscopic current loops. Outside the material, an assembly of such microscopic current loops is not different from a macroscopic current circulating around the material's surface, despite the fact that no individual magnetic moment is traveling a large distance. These bound currents can be described using the magnetization M.
The very complicated and granular bound charges and bound currents, therefore can be represented on the macroscopic scale in terms of P and M which average these charges and currents on a sufficiently large scale so as not to see the granularity of individual atoms, but also sufficiently small that they vary with location in the material. As such, the Maxwell's macroscopic equations ignores many details on a fine scale that may be unimportant to understanding matters on a grosser scale by calculating fields that are averaged over some suitably sized volume.
Equations
| Name | Differential form | Integral form |
|---|---|---|
| Gauss's law | 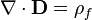 |
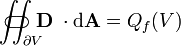 |
| Gauss's law for magnetism | 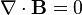 |
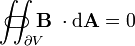 |
| Maxwell–Faraday equation ( Faraday's law of induction) |
 |
 |
| Ampère's circuital law (with Maxwell's correction) |
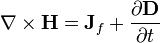 |
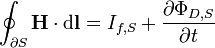 |
Constitutive relations
In order to apply 'Maxwell's macroscopic equations', it is necessary to specify the relations between displacement field D and E, and the magnetic H-field H and B. These equations specify the response of bound charge and current to the applied fields and are called constitutive relations.
Determining the constitutive relationship between the auxiliary fields D and H and the E and B fields starts with the definition of the auxiliary fields themselves:
where P is the polarization field and M is the magnetization field which are defined in terms of microscopic bound charges and bound current respectively. Before getting to how to calculate M and P it is useful to examine some special cases, though.
Without magnetic or dielectric materials
In the absence of magnetic or dielectric materials, the constitutive relations are simple:
where ε0 and μ0 are two universal constants, called the permittivity of free space and permeability of free space, respectively. Substituting these back into Maxwell's macroscopic equations lead directly to Maxwell's microscopic equations, except that the currents and charges are replaced with free currents and free charges. This is expected since there are no bound charges nor currents.
Isotropic Linear materials
In an ( isotropic) linear material, where P is proportional to E and M is proportional to B the constitutive relations are also straightforward. In terms of the polarizaton P and the magnetization M they are:
where χe and χm are the electric and magnetic susceptibilities of a given material respectively. In terms of D and H the constitutive relations are:
where ε and μ are constants (which depend on the material), called the permittivity and permeability, respectively, of the material. These are related to the susceptibilities by:
Substituting in the constitutive relations above into Maxwell's equations in linear, dispersionless, time-invariant materials (differential form only) are:
These are formally identical to the general formulation in terms of E and B (given above), except that the permittivity of free space was replaced with the permittivity of the material, the permeability of free space was replaced with the permeability of the material, and only free charges and currents are included (instead of all charges and currents). Unless that material is homogeneous in space, ε and μ cannot be factored out of the derivative expressions on the left sides.
General case
For real-world materials, the constitutive relations are not linear, except approximately. Calculating the constitutive relations from first principles involves determining how P and M are created from a given E and B. These relations may be empirical (based directly upon measurements), or theoretical (based upon statistical mechanics, transport theory or other tools of condensed matter physics). The detail employed may be macroscopic or microscopic, depending upon the level necessary to the problem under scrutiny.
In general, though the constitutive relations can usually still be written:
but ε and μ are not, in general, simple constants, but rather functions. Examples are:
- Dispersion and absorption where ε and μ are functions of frequency. (Causality does not permit materials to be nondispersive; see, for example, Kramers–Kronig relations). Neither do the fields need to be in phase which leads to ε and μ being complex. This also leads to absorption.
- Bi-(an)isotropy where H and D depend on both B and E:
- Nonlinearity where ε and μ are functions of E and B.
- Anisotropy (such as birefringence or dichroism) which occurs when ε and μ are second-rank tensors,
- Dependence of P and M on E and B at other locations and times. This could be due to spatial inhomogeneity; for example in a domained structure, heterostructure or a liquid crystal, or most commonly in the situation where there are simply multiple materials occupying different regions of space). Or it could be due to a time varying medium or due to hysteresis. In such cases P and M can be calculated as:
- in which the permittivity and permeability functions are replaced by integrals over the more general electric and magnetic susceptibilities.
In practice, some materials properties have a negligible impact in particular circumstances, permitting neglect of small effects. For example: optical nonlinearities can be neglected for low field strengths; material dispersion is unimportant when frequency is limited to a narrow bandwidth; material absorption can be neglected for wavelengths for which a material is transparent; and metals with finite conductivity often are approximated at microwave or longer wavelengths as perfect metals with infinite conductivity (forming hard barriers with zero skin depth of field penetration).
It may be noted that man-made materials can be designed to have customized permittivity and permeability, such as metamaterials and photonic crystals.
Calculation of constitutive relations
In general, the constitutive equations are theoretically determined by calculating how a molecule responds to the local fields through the Lorentz force. Other forces may need to be modeled as well such as lattice vibrations in crystals or bond forces. Including all of the forces leads to changes in the molecule which are used to calculate P and M as a function of the local fields.
The local fields differ from the applied fields due to the fields produced by the polarization and magnetization of nearby material; an effect which also needs to be modeled. Further, real materials are not continuous media; the local fields of real materials vary wildly on the atomic scale. The fields need to be averaged over a suitable volume to form a continuum approximation.
These continuum approximations often require some type of quantum mechanical analysis such as quantum field theory as applied to condensed matter physics. See, for example, density functional theory, Green–Kubo relations and Green's function. Various approximate transport equations have evolved, for example, the Boltzmann equation or the Fokker–Planck equation or the Navier–Stokes equations. Some examples where these equations are applied are magnetohydrodynamics, fluid dynamics, electrohydrodynamics, superconductivity, plasma modeling. An entire physical apparatus for dealing with these matters has developed. A different set of homogenization methods (evolving from a tradition in treating materials such as conglomerates and laminates) are based upon approximation of an inhomogeneous material by a homogeneous effective medium (valid for excitations with wavelengths much larger than the scale of the inhomogeneity).
The theoretical modeling of the continuum-approximation properties of many real materials often rely upon measurement as well, for example, ellipsometry measurements.
History
Relation between electricity, magnetism, and the speed of light
The relation between electricity, magnetism, and the speed of light can be summarized by the modern equation:
The left-hand side is the speed of light, and the right-hand side is a quantity related to the equations governing electricity and magnetism. Although the right-hand side has units of velocity, it can be inferred from measurements of electric and magnetic forces, which involve no physical velocities. Therefore, establishing this relationship provided convincing evidence that light is an electromagnetic phenomenon.
The discovery of this relationship started in 1855, when Wilhelm Eduard Weber and Rudolf Kohlrausch determined that there was a quantity related to electricity and magnetism, "the ratio of the absolute electromagnetic unit of charge to the absolute electrostatic unit of charge" (in modern language, the value 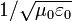 ), and determined that it should have units of velocity. They then measured this ratio by an experiment which involved charging and discharging a Leyden jar and measuring the magnetic force from the discharge current, and found a value 3.107×108 m/s, remarkably close to the speed of light, which had recently been measured at 3.14×108 m/s by Hippolyte Fizeau in 1848 and at 2.98×108 m/s by Léon Foucault in 1850. However, Weber and Kohlrausch did not make the connection to the speed of light. Towards the end of 1861 while working on part III of his paper On Physical Lines of Force, Maxwell travelled from Scotland to London and looked up Weber and Kohlrausch's results. He converted them into a format which was compatible with his own writings, and in doing so he established the connection to the speed of light and concluded that light is a form of electromagnetic radiation.
), and determined that it should have units of velocity. They then measured this ratio by an experiment which involved charging and discharging a Leyden jar and measuring the magnetic force from the discharge current, and found a value 3.107×108 m/s, remarkably close to the speed of light, which had recently been measured at 3.14×108 m/s by Hippolyte Fizeau in 1848 and at 2.98×108 m/s by Léon Foucault in 1850. However, Weber and Kohlrausch did not make the connection to the speed of light. Towards the end of 1861 while working on part III of his paper On Physical Lines of Force, Maxwell travelled from Scotland to London and looked up Weber and Kohlrausch's results. He converted them into a format which was compatible with his own writings, and in doing so he established the connection to the speed of light and concluded that light is a form of electromagnetic radiation.
The term Maxwell's equations
The four modern Maxwell's equations can be found individually throughout his 1861 paper, derived theoretically using a molecular vortex model of Michael Faraday's "lines of force" and in conjunction with the experimental result of Weber and Kohlrausch. But it wasn't until 1884 that Oliver Heaviside, concurrently with similar work by Willard Gibbs and Heinrich Hertz, grouped the four together into a distinct set. This group of four equations was known variously as the Hertz-Heaviside equations and the Maxwell-Hertz equations, and are sometimes still known as the Maxwell–Heaviside equations.
Maxwell's contribution to science in producing these equations lies in the correction he made to Ampère's circuital law in his 1861 paper On Physical Lines of Force. He added the displacement current term to Ampère's circuital law and this enabled him to derive the electromagnetic wave equation in his later 1865 paper A Dynamical Theory of the Electromagnetic Field and demonstrate the fact that light is an electromagnetic wave. This fact was then later confirmed experimentally by Heinrich Hertz in 1887. The physicist Richard Feynman predicted that, "The American Civil War will pale into provincial insignificance in comparison with this important scientific event of the same decade."
The concept of fields was introduced by, among others, Faraday. Albert Einstein wrote:
The precise formulation of the time-space laws was the work of Maxwell. Imagine his feelings when the differential equations he had formulated proved to him that electromagnetic fields spread in the form of polarised waves, and at the speed of light! To few men in the world has such an experience been vouchsafed ... it took physicists some decades to grasp the full significance of Maxwell's discovery, so bold was the leap that his genius forced upon the conceptions of his fellow-workers—(Science, May 24, 1940)
Heaviside worked to eliminate the potentials ( electric potential and magnetic potential) that Maxwell had used as the central concepts in his equations; this effort was somewhat controversial, though it was understood by 1884 that the potentials must propagate at the speed of light like the fields, unlike the concept of instantaneous action-at-a-distance like the then conception of gravitational potential. Modern analysis of, for example, radio antennas, makes full use of Maxwell's vector and scalar potentials to separate the variables, a common technique used in formulating the solutions of differential equations. However the potentials can be introduced by algebraic manipulation of the four fundamental equations.
On Physical Lines of Force
The four modern day Maxwell's equations appeared throughout Maxwell's 1861 paper On Physical Lines of Force:
- Equation (56) in Maxwell's 1861 paper is ∇ ⋅ B = 0.
- Equation (112) is Ampère's circuital law with Maxwell's displacement current added. It is the addition of displacement current that is the most significant aspect of Maxwell's work in electromagnetism, as it enabled him to later derive the electromagnetic wave equation in his 1865 paper A Dynamical Theory of the Electromagnetic Field, and hence show that light is an electromagnetic wave. It is therefore this aspect of Maxwell's work which gives the equations their full significance. (Interestingly, Kirchhoff derived the telegrapher's equations in 1857 without using displacement current. But he did use Poisson's equation and the equation of continuity which are the mathematical ingredients of the displacement current. Nevertheless, Kirchhoff believed his equations to be applicable only inside an electric wire and so he is not credited with having discovered that light is an electromagnetic wave).
- Equation (115) is Gauss's law.
- Equation (54) is an equation that Oliver Heaviside referred to as 'Faraday's law'. This equation caters for the time varying aspect of electromagnetic induction, but not for the motionally induced aspect, whereas Faraday's original flux law caters for both aspects. Maxwell deals with the motionally dependent aspect of electromagnetic induction, v × B, at equation (77). Equation (77) which is the same as equation (D) in the original eight Maxwell's equations listed below, corresponds to all intents and purposes to the modern day force law F = q( E + v × B ) which sits adjacent to Maxwell's equations and bears the name Lorentz force, even though Maxwell derived it when Lorentz was still a young boy.
The difference between the B and the H vectors can be traced back to Maxwell's 1855 paper entitled On Faraday's Lines of Force which was read to the Cambridge Philosophical Society. The paper presented a simplified model of Faraday's work, and how the two phenomena were related. He reduced all of the current knowledge into a linked set of differential equations.

It is later clarified in his concept of a sea of molecular vortices that appears in his 1861 paper On Physical Lines of Force. Within that context, H represented pure vorticity (spin), whereas B was a weighted vorticity that was weighted for the density of the vortex sea. Maxwell considered magnetic permeability µ to be a measure of the density of the vortex sea. Hence the relationship,
- Magnetic induction current causes a magnetic current density
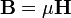
was essentially a rotational analogy to the linear electric current relationship,
- Electric convection current
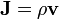
where ρ is electric charge density. B was seen as a kind of magnetic current of vortices aligned in their axial planes, with H being the circumferential velocity of the vortices. With µ representing vortex density, it follows that the product of µ with vorticity H leads to the magnetic field denoted as B.
The electric current equation can be viewed as a convective current of electric charge that involves linear motion. By analogy, the magnetic equation is an inductive current involving spin. There is no linear motion in the inductive current along the direction of the B vector. The magnetic inductive current represents lines of force. In particular, it represents lines of inverse square law force.
The extension of the above considerations confirms that where B is to H, and where J is to ρ, then it necessarily follows from Gauss's law and from the equation of continuity of charge that E is to D. i.e. B parallels with E, whereas H parallels with D.
A Dynamical Theory of the Electromagnetic Field
In 1864 Maxwell published A Dynamical Theory of the Electromagnetic Field in which he showed that light was an electromagnetic phenomenon. Confusion over the term "Maxwell's equations" is exacerbated because it is also sometimes used for a set of eight equations that appeared in Part III of Maxwell's 1864 paper A Dynamical Theory of the Electromagnetic Field, entitled "General Equations of the Electromagnetic Field," a confusion compounded by the writing of six of those eight equations as three separate equations (one for each of the Cartesian axes), resulting in twenty equations and twenty unknowns. (As noted above, this terminology is not common: Modern references to the term "Maxwell's equations" refer to the Heaviside restatements.)
The eight original Maxwell's equations can be written in modern vector notation as follows:
- (A) The law of total currents
- (B) The equation of magnetic force
- (C) Ampère's circuital law
- (D) Electromotive force created by convection, induction, and by static electricity. (This is in effect the Lorentz force)
- (E) The electric elasticity equation
- (F) Ohm's law
- (G) Gauss's law
- (H) Equation of continuity
or
- Notation
- H is the magnetizing field, which Maxwell called the magnetic intensity.
- J is the current density (withJtot being the total current including displacement current).
- D is the displacement field (called the electric displacement by Maxwell).
- ρ is the free charge density (called the quantity of free electricity by Maxwell).
- A is the magnetic potential (called the angular impulse by Maxwell).
- E is called the electromotive force by Maxwell. The term electromotive force is nowadays used for voltage, but it is clear from the context that Maxwell's meaning corresponded more to the modern term electric field.
- φ is the electric potential (which Maxwell also called electric potential).
- σ is the electrical conductivity (Maxwell called the inverse of conductivity the specific resistance, what is now called the resistivity).
It is interesting to note the μv × H term that appears in equation D. Equation D is therefore effectively the Lorentz force, similarly to equation (77) of his 1861 paper (see above).
When Maxwell derives the electromagnetic wave equation in his 1865 paper, he uses equation D to cater for electromagnetic induction rather than Faraday's law of induction which is used in modern textbooks. (Faraday's law itself does not appear among his equations.) However, Maxwell drops the μv × H term from equation D when he is deriving the electromagnetic wave equation, as he considers the situation only from the rest frame.
A Treatise on Electricity and Magnetism
In A Treatise on Electricity and Magnetism, an 1873 treatise on electromagnetism written by James Clerk Maxwell, eleven general equations of the electromagnetic field are listed and these include the eight that are listed in the 1865 paper.
Maxwell's equations and relativity
Maxwell's original equations are based on the idea that light travels through a sea of molecular vortices known as the 'luminiferous aether', and that the speed of light has to be respective to the reference frame of this aether. Measurements designed to measure the speed of the Earth through the aether conflicted, though.
A more theoretical approach was suggested by Hendrik Lorentz along with George FitzGerald and Joseph Larmor. Both Larmor (1897) and Lorentz (1899, 1904) derived the Lorentz transformation (so named by Henri Poincaré) as one under which Maxwell's equations were invariant. Poincaré (1900) analyzed the coordination of moving clocks by exchanging light signals. He also established mathematically the group property of the Lorentz transformation (Poincaré 1905).
Einstein dismissed the aether as unnecessary and concluded that Maxwell's equations predict the existence of a fixed speed of light, independent of the speed of the observer, and as such he used Maxwell's equations as the starting point for his special theory of relativity. In doing so, he established the Lorentz transformation as being valid for all matter and not just Maxwell's equations. Maxwell's equations played a key role in Einstein's famous paper on special relativity; for example, in the opening paragraph of the paper, he motivated his theory by noting that a description of a conductor moving with respect to a magnet must generate a consistent set of fields irrespective of whether the force is calculated in the rest frame of the magnet or that of the conductor.
General relativity has also had a close relationship with Maxwell's equations. For example, Theodor Kaluza and Oskar Klein showed in the 1920s that Maxwell's equations can be derived by extending general relativity into five dimensions. This strategy of using higher dimensions to unify different forces remains an active area of research in particle physics.
Modified to include magnetic monopoles
Maxwell's equations of electromagnetism relate the electric and magnetic fields to the motions of electric charges. The standard form of the equations provide for an electric charge, but posit no magnetic charge. There is no known magnetic analog of an electron, however recently scientists have described behavior in a crystalline state of matter known as spin-ice which have macroscopic behaviour like magnetic monopoles. (in accordance with the fact that magnetic charge has never been seen and may not exist). Except for this, the equations are symmetric under interchange of electric and magnetic field. In fact, symmetric equations can be written when all charges are zero, and this is how the wave equation is derived (see immediately above).
Fully symmetric equations can also be written if one allows for the possibility of magnetic charges. With the inclusion of a variable for these magnetic charges, say ρm, there will also be a "magnetic current" variable in the equations, Jm. The extended Maxwell's equations (in cgs-Gaussian units) are as follows:
-
Name Without magnetic monopoles With magnetic monopoles (hypothetical) Gauss's law: 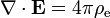
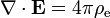
Gauss's law for magnetism: 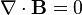
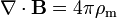
Maxwell–Faraday equation
( Faraday's law of induction):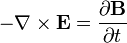
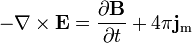
Ampère's law
(with Maxwell's extension):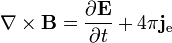
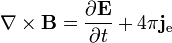
If magnetic charges do not exist, or if they exist but where they are not present in a region, then the new variables are zero, and the symmetric equations reduce to the conventional equations of electromagnetism such as ∇ · B = 0.
Boundary conditions using Maxwell's equations
Like all sets of differential equations, Maxwell's equations cannot be uniquely solved without a suitable set of boundary conditions and initial conditions.
For example, consider a region with no charges and no currents. One particular solution that satisfies all of Maxwell's equations in that region is that both E and B = 0 everywhere in the region. This solution is obviously false if there is a charge just outside of the region. In this particular example, all of the electric and magnetic fields in the interior are due to the charges outside of the volume. Different charges outside of the volume produce different fields on the surface of that volume and therefore have a different boundary conditions. In general, knowing the appropriate boundary conditions for a given region along with the currents and charges in that region allows one to solve for all the fields everywhere within that region. An example of this type is a an electromagnetic scattering problem, where an electromagnetic wave originating outside the scattering region is scattered by a target, and the scattered electromagnetic wave is analyzed for the information it contains about the target by virtue of the interaction with the target during scattering.
In some cases, like waveguides or cavity resonators, the solution region is largely isolated from the universe, for example, by metallic walls, and boundary conditions at the walls define the fields with influence of the outside world confined to the input/output ends of the structure. In other cases, the universe at large sometimes is approximated by an artificial absorbing boundary, or, for example for radiating antennas or communication satellites, these boundary conditions can take the form of asymptotic limits imposed upon the solution. In addition, for example in an optical fibre or thin-film optics, the solution region often is broken up into subregions with their own simplified properties, and the solutions in each subregion must be joined to each other across the subregion interfaces using boundary conditions. A particular example of this use of boundary conditions is the replacement of a material with a volume polarization by a charged surface layer, or of a material with a volume magnetization by a surface current, as described in the section Bound charge and current.
Following are some links of a general nature concerning boundary value problems: Examples of boundary value problems, Sturm–Liouville theory, Dirichlet boundary condition, Neumann boundary condition, mixed boundary condition, Cauchy boundary condition, Sommerfeld radiation condition. Needless to say, one must choose the boundary conditions appropriate to the problem being solved. See also Kempel and the book by Friedman.
Gaussian units
Gaussian units is a popular electromagnetism variant of the centimetre gram second system of units (cgs). In gaussian units, Maxwell's equations are:
where c is the speed of light in a vacuum. The microscopic equations are:
The relation between electric displacement field, electric field and polarization density is:
And likewise the relation between magnetic induction, magnetic field and total magnetization is:
In the linear approximation, the electric susceptibility and magnetic susceptibility are defined so that:
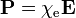 ,
, 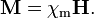
(Note: although the susceptibilities are dimensionless numbers in both cgs and SI, they differ in value by a factor of 4π.) The permittivity and permeability are:
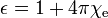 ,
, 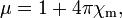
so that
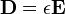 ,
, 
In vacuum, ε = μ = 1, therefore D = E, and B = H.
The force exerted upon a charged particle by the electric field and magnetic field is given by the Lorentz force equation:
where q is the charge on the particle and v is the particle velocity. This is slightly different from the SI-unit expression above. For example, the magnetic field B has the same units as the electric field E.
Some equations in the article are given in Gaussian units but not SI or vice-versa. Fortunately, there are general rules to convert from one to the other; see the article Gaussian units for details.
Alternative formulations of Maxwell's equations
Special relativity motivated a compact mathematical formulation of Maxwell's equations, in terms of covariant tensors. Quantum mechanics also motivated other formulations.
For example, consider a conductor moving in the field of a magnet. In the frame of the magnet, that conductor experiences a magnetic force. But in the frame of a conductor moving relative to the magnet, the conductor experiences a force due to an electric field. The following formulation shows how Maxwell's equations take the same form in any inertial coordinate system.
Covariant formulation of Maxwell's equations
In special relativity, in order to more clearly express the fact that Maxwell's ('microscopic') equations take the same form in any inertial coordinate system, Maxwell's equations are written in terms of four-vectors and tensors in the "manifestly covariant" form. The purely spatial components of the following are in SI units.
One ingredient in this formulation is the electromagnetic tensor, a rank-2 covariant antisymmetric tensor combining the electric and magnetic fields:
and the result of raising its indices
The other ingredient is the four-current:
where ρ is the charge density and J is the current density.
With these ingredients, Maxwell's equations can be written:
and
The first tensor equation is an expression of the two inhomogeneous Maxwell's equations, Gauss's law and Ampere's law with Maxwell's correction. The second equation is an expression of the two homogeneous equations, Faraday's law of induction and Gauss's law for magnetism. The second equation is equivalent to
where 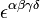 is the contravariant version of the Levi-Civita symbol, and
is the contravariant version of the Levi-Civita symbol, and
is the 4-gradient. In the tensor equations above, repeated indices are summed over according to Einstein summation convention. We have displayed the results in several common notations. Upper and lower components of a vector, vα and vα respectively, are interchanged with the fundamental tensor g, e.g., g = η = diag(−1, +1, +1, +1).
Alternative covariant presentations of Maxwell's equations also exist, for example in terms of the four-potential; see Covariant formulation of classical electromagnetism for details.
Potential formulation
In advanced classical mechanics and in quantum mechanics (where it is necessary) it is sometimes useful to express Maxwell's equations in a 'potential formulation' involving the electric potential (also called scalar potential), φ, and the magnetic potential, A, (also called vector potential). These are defined such that:
With these definitions, the two homogeneous Maxwell's equations (Faraday's Law and Gauss's law for magnetism) are automatically satisfied and the other two (inhomogeneous) equations give the following equations (for "Maxwell's microscopic equations"):
These equations, taken together, are as powerful and complete as Maxwell's equations. Moreover, if we work only with the potentials and ignore the fields, the problem has been reduced somewhat, as the electric and magnetic fields each have three components which need to be solved for (six components altogether), while the electric and magnetic potentials have only four components altogether.
Many different choices of A and φ are consistent with a given E and B, making these choices physically equivalent – a flexibility known as gauge freedom. Suitable choice of A and φ can simplify these equations, or can adapt them to suit a particular situation.
Four-potential
In the Lorentz gauge, the two equations that represent the potentials can be reduced to one manifestly Lorentz invariant equation, using four-vectors: the four-current defined by
formed from the current density j and charge density ρ, and the electromagnetic four-potential defined by
formed from the vector potential A and the scalar potential 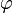 . The resulting single equation, due to Arnold Sommerfeld, a generalization of an equation due to Bernhard Riemann and known as the Riemann–Sommerfeld equation or the covariant form of the Maxwell equations, is:
. The resulting single equation, due to Arnold Sommerfeld, a generalization of an equation due to Bernhard Riemann and known as the Riemann–Sommerfeld equation or the covariant form of the Maxwell equations, is:
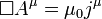 ,
,
where 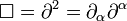 is the d'Alembertian operator, or four-Laplacian,
is the d'Alembertian operator, or four-Laplacian, 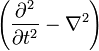 , sometimes written
, sometimes written 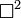 , or
, or  , where
, where  is the four-gradient.
is the four-gradient.
Differential formulations
In free space, where ε = ε0 and μ = μ0 are constant everywhere, Maxwell's equations simplify considerably once the language of differential geometry and differential forms is used. In what follows, cgs-Gaussian units, not SI units are used. (To convert to SI, see here.) The electric and magnetic fields are now jointly described by a 2-form F in a 4-dimensional spacetime manifold. Maxwell's equations then reduce to the Bianchi identity
where d denotes the exterior derivative — a natural coordinate and metric independent differential operator acting on forms — and the source equation
where the (dual) Hodge star operator * is a linear transformation from the space of 2-forms to the space of (4-2)-forms defined by the metric in Minkowski space (in four dimensions even by any metric conformal to this metric), and the fields are in natural units where 1/4πε0 = 1. Here, the 3-form J is called the electric current form or current 3-form satisfying the continuity equation
The current 3-form can be integrated over a 3-dimensional space-time region. The physical interpretation of this integral is the charge in that region if it is spacelike, or the amount of charge that flows through a surface in a certain amount of time if that region is a spacelike surface cross a timelike interval. As the exterior derivative is defined on any manifold, the differential form version of the Bianchi identity makes sense for any 4-dimensional manifold, whereas the source equation is defined if the manifold is oriented and has a Lorentz metric. In particular the differential form version of the Maxwell equations are a convenient and intuitive formulation of the Maxwell equations in general relativity.
In a linear, macroscopic theory, the influence of matter on the electromagnetic field is described through more general linear transformation in the space of 2-forms. We call
the constitutive transformation. The role of this transformation is comparable to the Hodge duality transformation. The Maxwell equations in the presence of matter then become:
where the current 3-form J still satisfies the continuity equation dJ = 0.
When the fields are expressed as linear combinations (of exterior products) of basis forms θp,
the constitutive relation takes the form
where the field coefficient functions are antisymmetric in the indices and the constitutive coefficients are antisymmetric in the corresponding pairs. In particular, the Hodge duality transformation leading to the vacuum equations discussed above are obtained by taking
which up to scaling is the only invariant tensor of this type that can be defined with the metric.
In this formulation, electromagnetism generalises immediately to any 4-dimensional oriented manifold or with small adaptations any manifold, requiring not even a metric. Thus the expression of Maxwell's equations in terms of differential forms leads to a further notational and conceptual simplification. Whereas Maxwell's Equations could be written as two tensor equations instead of eight scalar equations, from which the propagation of electromagnetic disturbances and the continuity equation could be derived with a little effort, using differential forms leads to an even simpler derivation of these results.
Conceptual insight from this formulation
On the conceptual side, from the point of view of physics, this shows that the second and third Maxwell equations should be grouped together, be called the homogeneous ones, and be seen as geometric identities expressing nothing else than: the field F derives from a more "fundamental" potential A. While the first and last one should be seen as the dynamical equations of motion, obtained via the Lagrangian principle of least action, from the "interaction term" A J (introduced through gauge covariant derivatives), coupling the field to matter.
Often, the time derivative in the third law motivates calling this equation "dynamical", which is somewhat misleading; in the sense of the preceding analysis, this is rather an artifact of breaking relativistic covariance by choosing a preferred time direction. To have physical degrees of freedom propagated by these field equations, one must include a kinetic term F *F for A; and take into account the non-physical degrees of freedom which can be removed by gauge transformation A → A' = A − dα. See also gauge fixing and Faddeev–Popov ghosts.
Geometric Algebra (GA) formulation
In geometric algebra, Maxwell's equations are reduced to a single equation,
where F and J are multivectors
and
with the unit pseudoscalar I2 = −1
The GA spatial gradient operator ∇ acts on a vector field, such that
In spacetime algebra using the same geometric product the equation is simply
the spacetime derivative of the electromagnetic field is its source. Here the (non-bold) spacetime gradient
is a four vector, as is the current density
For a demonstration that the equations given reproduce Maxwell's equations see the main article.
Classical electrodynamics as the curvature of a line bundle
An elegant and intuitive way to formulate Maxwell's equations is to use complex line bundles or principal bundles with fibre U(1). The connection  on the line bundle has a curvature
on the line bundle has a curvature  which is a two-form that automatically satisfies
which is a two-form that automatically satisfies 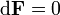 and can be interpreted as a field-strength. If the line bundle is trivial with flat reference connection d we can write
and can be interpreted as a field-strength. If the line bundle is trivial with flat reference connection d we can write 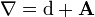 and F = dA with A the 1-form composed of the electric potential and the magnetic vector potential.
and F = dA with A the 1-form composed of the electric potential and the magnetic vector potential.
In quantum mechanics, the connection itself is used to define the dynamics of the system. This formulation allows a natural description of the Aharonov-Bohm effect. In this experiment, a static magnetic field runs through a long magnetic wire (e.g., an iron wire magnetized longitudinally). Outside of this wire the magnetic induction is zero, in contrast to the vector potential, which essentially depends on the magnetic flux through the cross-section of the wire and does not vanish outside. Since there is no electric field either, the Maxwell tensor F = 0 throughout the space-time region outside the tube, during the experiment. This means by definition that the connection  is flat there.
is flat there.
However, as mentioned, the connection depends on the magnetic field through the tube since the holonomy along a non-contractible curve encircling the tube is the magnetic flux through the tube in the proper units. This can be detected quantum-mechanically with a double-slit electron diffraction experiment on an electron wave traveling around the tube. The holonomy corresponds to an extra phase shift, which leads to a shift in the diffraction pattern.
Curved spacetime
Traditional formulation
Matter and energy generate curvature of spacetime. This is the subject of general relativity. Curvature of spacetime affects electrodynamics. An electromagnetic field having energy and momentum also generates curvature in spacetime. Maxwell's equations in curved spacetime can be obtained by replacing the derivatives in the equations in flat spacetime with covariant derivatives. (Whether this is the appropriate generalization requires separate investigation.) The sourced and source-free equations become ( cgs-Gaussian units):
and
Here,
is a Christoffel symbol that characterizes the curvature of spacetime and Dγ is the covariant derivative.
Formulation in terms of differential forms
The formulation of the Maxwell equations in terms of differential forms can be used without change in general relativity. The equivalence of the more traditional general relativistic formulation using the covariant derivative with the differential form formulation can be seen as follows. Choose local coordinates xα which gives a basis of 1-forms dxα in every point of the open set where the coordinates are defined. Using this basis and cgs-Gaussian units we define
- The antisymmetric infinitesimal field tensor
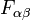 , corresponding to the field 2-form F
, corresponding to the field 2-form F
- The current-vector infinitesimal 3-form J
Here g is as usual the determinant of the metric tensor 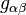 . A small computation that uses the symmetry of the Christoffel symbols (i.e., the torsion-freeness of the Levi Civita connection) and the covariant constantness of the Hodge star operator then shows that in this coordinate neighbourhood we have:
. A small computation that uses the symmetry of the Christoffel symbols (i.e., the torsion-freeness of the Levi Civita connection) and the covariant constantness of the Hodge star operator then shows that in this coordinate neighbourhood we have:
- the Bianchi identity
- the source equation
- the continuity equation