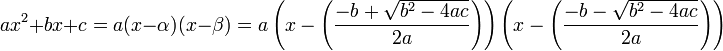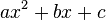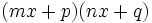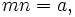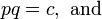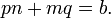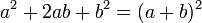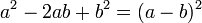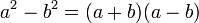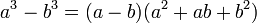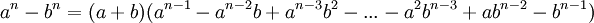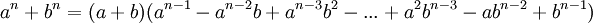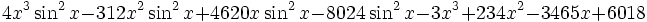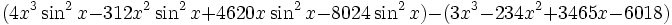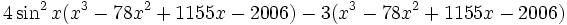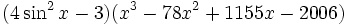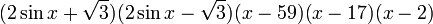Factorization
Background Information
SOS Children has tried to make Wikipedia content more accessible by this schools selection. To compare sponsorship charities this is the best sponsorship link.
In mathematics, factorization (also factorisation in British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.
The aim of factoring is usually to reduce something to "basic building blocks," such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra.
The opposite of factorization is expansion. This is the process of multiplying together factors to recreate the original, "expanded" polynomial.
Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.
A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.
Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function.
Prime factorization of an integer
By the fundamental theorem of arithmetic, every positive integer has a unique prime factorization. Given an algorithm for integer factorization, one can factor any integer down to its constituent primes by repeated application of this algorithm. For very large numbers, no efficient algorithm is known. For smaller numbers, however, there are a variety of different algorithms that can be applied.
Factoring a quadratic polynomial
Any quadratic polynomial over the complex numbers (polynomials of the form 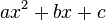 where
where 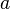 ,
, 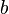 , and
, and  ∈
∈ 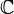 ) can be factored into an expression with the form
) can be factored into an expression with the form  using the quadratic formula. The method is as follows:
using the quadratic formula. The method is as follows:
where 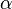 and
and 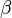 are the two roots of the polynomial, found with the quadratic formula.
are the two roots of the polynomial, found with the quadratic formula.
Polynomials factorable over the integers
Quadratic polynomials can sometimes be factored into two binomials with simple integer coefficients, without the need to use the quadratic formula. In a quadratic equation, this will expose its two roots. The formula
would be factored into:
where
You can then set each binomial equal to zero, and solve for x to reveal the two roots. Factoring does not involve any other formulas, and is mostly just something you see when you come upon a quadratic equation.
Take for example 2x2 − 5x + 2 = 0. Because a = 2 and mn = a, mn = 2, which means that of m and n, one is 1 and the other is 2. Now we have (2x + p)(x + q) = 0. Because c = 2 and pq = c, pq = 2, which means that of p and q, one is 1 and the other is 2 or one is −1 and the other is −2. A guess and check of substituting the 1 and 2, and −1 and −2, into p and q (while applying pn + mq = b) tells us that 2x2 − 5x + 2 = 0 factors into (2x − 1)(x − 2) = 0, giving us the roots x = {0.5, 2}
If a polynomial with integer coefficients has a discriminant that is a perfect square, that polynomial is factorable over the integers.
For example, look at the polynomial 2x2 + 2x - 12. If you substitute the values of the expression into the quadratic formula, the discriminant 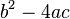 becomes 22 - 4 × 2 × -12, which equals 100. 100 is a perfect square, so the polynomial 2x2 + 2x - 12 is factorable over the integers; its factors are 2, (x - 2), and (x + 3).
becomes 22 - 4 × 2 × -12, which equals 100. 100 is a perfect square, so the polynomial 2x2 + 2x - 12 is factorable over the integers; its factors are 2, (x - 2), and (x + 3).
Now look at the polynomial x2 + 93x - 2. Its discriminant, 932 - 4 × 1 × -2, is equal to 8657, which is not a perfect square. So x2 + 93x - 2 cannot be factored over the integers.
Perfect square trinomials
Some quadratics can be factored into two identical binomials. These quadratics are called perfect square trinomials. Perfect square trinomials can be factored as follows:
Sum/difference of two squares
Another common type of algebraic factoring is called the difference of two squares. It is the application of the formula
to any two terms, whether or not they are perfect squares. If the two terms are subtracted, simply apply the formula. If they are added, the two binomials obtained from the factoring will each have an imaginary term. This formula can be represented as
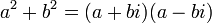 .
.
For example, 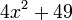 can be factored into
can be factored into 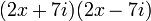 .
.
Factoring other polynomials
Sum/difference of two cubes
Another less-used but still common formula for factoring is the sum or difference of two cubes. The sum can be represented by
and the difference by
For example, x3 − 103 (or x3 − 1000) can be factored into (x − 10)(x2 + 10x + 100).
Sum/difference of any two numbers raised to the same power
In general, 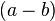 is a factor of
is a factor of  where
where 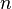 is a positive integer. So,
is a positive integer. So,
Also, 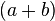 is a factor of
is a factor of  where
where 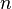 is a positive even integer. Such that,
is a positive even integer. Such that,
Likewise, 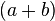 is a factor of
is a factor of  where
where 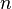 is a positive odd integer. So that,
is a positive odd integer. So that,
Factoring by grouping
Another way to factor some equations is factoring by grouping. This is done by placing the terms in an expression into two or more groups, where each group can be factored by a known method. The results of these factorizations can sometimes be combined to make an even more simplified expression.
For example, suppose you had the expression
which upon first glance looks like an unwieldy expression. One logical step, if you decide to factor by grouping, would be to combine all of the expressions with 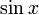 and all without
and all without 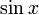 . Then you would have the expression
. Then you would have the expression
where each of the two groups can be factored giving us
This can be further simplified into
when can then be factored into
and finally
which is the expression in fully factored form.
Other common formulas
There are many additional formulas that can be used to easily factor a polynomial. Some common ones are listed below.
| Expanded form | Factored form |
|---|---|
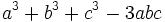 |
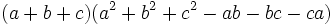 |
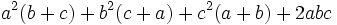 |
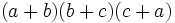 |
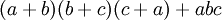 |
 |
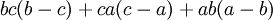 |
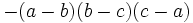 |
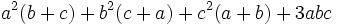 |
 |
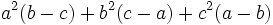 |
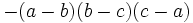 |
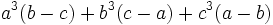 |
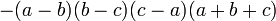 |
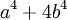 ( Sophie Germain's identity) ( Sophie Germain's identity) |
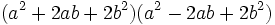 |
Factoring in mathematical logic
In mathematical logic and automated theorem proving, factoring is the technique of deriving a single, more specific atom from a disjunction of two more general unifiable atoms. For example, from ∀ X, Y : P(X, a) or P(b, Y) we can derive P(b, a).