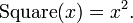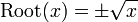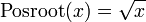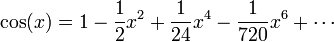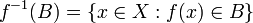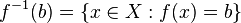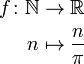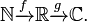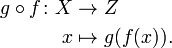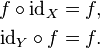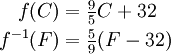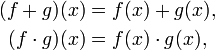Function (mathematics)
Background to the schools Wikipedia
This selection is made for schools by a children's charity read more. A quick link for child sponsorship is http://www.sponsor-a-child.org.uk/
The mathematical concept of a function expresses dependence between two quantities, one of which is given (the independent variable, argument of the function, or its "input") and the other produced (the dependent variable, value of the function, or "output"). A function associates a single output to each input element drawn from a fixed set, such as the real numbers.
There are many ways to give a function: by a formula, by a plot or graph, by an algorithm that computes it, by a description of its properties. Sometimes, a function is described through its relationship to other functions (see, for example, inverse function). In applied disciplines, functions are frequently specified by their tables of values or by a formula. Not all types of description can be given for every possible function, and one must make a firm distinction between the function itself and multiple ways of presenting or visualizing it.
One idea of enormous importance in all of mathematics is composition of functions: if z is a function of y and y is a function of x, then z is a function of x. We may describe it informally by saying that the composite function is obtained by using the output of the first function as the input of the second one. This feature of functions distinguishes them from other mathematical constructs, such as numbers or figures, and provides the theory of functions with its most powerful structure.
Introduction
Functions play a fundamental role in all areas of mathematics, as well as in other sciences and engineering. However, the intuition pertaining to functions, notation, and even the very meaning of the term "function" varies between the fields. More abstract areas of mathematics, such as set theory, consider very general types of functions, which may not be specified by a concrete rule and are not governed by any familiar principles. The characteristic property of a function in the most abstract sense is that it relates exactly one output to each of its admissible inputs. Such functions need not involve numbers and may, for example, associate each of a set of words with their own first letters.
Functions in algebra are usually expressible in terms of algebraic operations. Functions studied in analysis, such as the exponential function, may have additional properties arising from continuity of space, but in the most general case cannot be defined by a single formula. Analytic functions in complex analysis may be defined fairly concretely through their series expansions. On the other hand, in lambda calculus, function is a primitive concept, instead of being defined in terms of set theory. The terms transformation and mapping are often synonymous with function. In some contexts, however, they differ slightly. In the first case, the term transformation usually applies to functions whose inputs and outputs are elements of the same set or more general structure. Thus, we speak of linear transformations from a vector space into itself and of symmetry transformations of a geometric object or a pattern. In the second case, used to describe sets whose nature is arbitrary, the term mapping is the most general concept of function.
Mathematical functions are denoted frequently by letters, and the standard notation for the output of a function ƒ with the input x is ƒ(x). A function may be defined only for certain inputs, and the collection of all acceptable inputs of the function is called its domain. The set of all resulting outputs is called the range of the function. However, in many fields, it is also important to specify the codomain of a function, which contains the range, but need not be equal to it. The distinction between range and codomain lets us ask whether the two happen to be equal, which in particular cases may be a question of some mathematical interest.
For example, the expression ƒ(x) = x2 describes a function ƒ of a variable x, which, depending on the context, may be an integer, a real or complex number or even an element of a group. Let us specify that x is an integer; then this function relates each input, x, with a single output, x2, obtained from x by squaring. Thus, the input of 3 is related to the output of 9, the input of 1 to the output of 1, and the input of −2 to the output of 4, and we write ƒ(3) = 9, ƒ(1)=1, ƒ(−2)=4. Since every integer can be squared, the domain of this function consists of all integers, while its range is the set of perfect squares. If we choose integers as the codomain as well, we find that many numbers, such as 2, 3, and 6, are in the codomain but not the range.
It is a usual practice in mathematics to introduce functions with temporary names like ƒ; in the next paragraph we might define ƒ(x) = 2x+1, and then ƒ(3) = 7. When a name for the function is not needed, often the form y = x2 is used.
If we use a function often, we may give it a more permanent name as, for example,
The essential property of a function is that for each input there must be a unique output. Thus, for example, the formula
does not define a function of a positive real variable, because it assigns two outputs to each number: the square roots of 9 are 3 and −3. To make the square root a function, we must specify which square root to choose. The definition
for any positive input chooses the positive square root as an output.
As mentioned above, a function need not involve numbers. By way of examples, consider the function that associates with each word its first letter or the function that associates with each triangle its area.
Definitions
Because functions are used in so many areas of mathematics, and in so many different ways, no single definition of function has been universally adopted. Some definitions are elementary, while others use technical language that may obscure the intuitive notion. Nevertheless, the essential idea is the same in every definition.
One elementary definition is that
- A function is given by an arithmetic expression describing how one number depends on another.
An example of such a function is y = 5x−20x3+16x5, where the value of y depends on the value of x. This is entirely satisfactory for parts of elementary mathematics, but is too clumsy and restrictive for more advanced areas. For example, the cosine function used in trigonometry cannot be written in this way; the best we can do is an infinite series,
That said, if we are willing to accept series as an extended sense of "arithmetic expression", we have a definition that served mathematics reasonably well for hundreds of years.
Eventually the gradual transformation of intuitive "calculus" into formal "analysis" brought the need for a broader definition. The emphasis shifted from how a function was presented — as a formula or rule — to a more abstract concept. Part of the new foundation was the use of sets, so that functions were no longer restricted to numbers. Thus we can say that
- A function ƒ from a set X to a set Y associates to each element x in X an element y = ƒ(x) in Y.
Note that X and Y need not be different sets; it is possible to have a function from a set to itself. Although it is possible to interpret the term "associates" in this definition with a concrete rule for the association, it is essential to move beyond that restriction. For example, we can sometimes prove that a function with certain properties exists, yet not be able to give any explicit rule for the association. In fact, in some cases it is impossible to give an explicit rule producing a specific y for each x, even though such a function exists. In the context of functions defined on arbitrary sets, it is not even clear how the phrase "explicit rule" should be interpreted.
As functions take on new roles and find new uses, the relationship of the function to the sets requires more precision. Perhaps every element in Y is associated with some x, perhaps not. In some parts of mathematics, including recursion theory and functional analysis, it is convenient to allow values of x with no association (in this case, the term partial function is often used). To be able to discuss such distinctions, many authors split a function into three parts, each a set:
- A function ƒ is an ordered triple of sets (F,X,Y) with restrictions, where
- F (the graph) is a set of ordered pairs (x,y),
- X (the source) contains all the first elements of F and perhaps more, and
- Y (the target) contains all the second elements of F and perhaps more.
The most common restrictions are that F pairs each x with just one y, and that X is just the set of first elements of F and no more.
When no restrictions are placed on F, we speak of a relation between X and Y rather than a function. The relation is "single-valued" when the first restriction holds: (x,y1)∈F and (x,y2)∈F together imply y1 = y2. Relations that are not single valued are sometimes called multivalued functions. A relation is "total" when a second restriction holds: if x∈X then (x,y)∈F for some y. Thus we can also say that
- A function from X to Y is a single-valued, total relation between X and Y.
The range of F, and of ƒ, is the set of all second elements of F; it is often denoted by rng ƒ. The domain of F is the set of all first elements of F; it is often denoted by dom ƒ. There are two common definitions for the domain of ƒ some authors define it as the domain of F, while others define it as the source of F.
The target Y of ƒ is also called the codomain of ƒ, denoted by cod ƒ; and the range of ƒ is also called the image of ƒ, denoted by im ƒ. The notation ƒ:X→Y indicates that ƒ is a function with domain X and codomain Y.
Some authors omit the source and target as unnecessary data. Indeed, given only the graph F, one can construct a suitable triple by taking dom F to be the source and rng F to be the target; this automatically causes F to be total. However, most authors in advanced mathematics prefer the greater power of expression afforded by the triple, especially the distinction it allows between range and codomain.
Incidentally, the ordered pairs and triples we have used are not distinct from sets; we can easily represent them within set theory. For example, we can use {{x},{x,y}} for the pair (x,y). Then for a triple (x,y,z) we can use the pair ((x,y),z). An important construction is the Cartesian product of sets X and Y, denoted by X×Y, which is the set of all possible ordered pairs (x,y) with x∈X and y∈Y. We can also construct the set of all possible functions from set X to set Y, which we denote by either [X→Y] or YX.
We now have tremendous flexibility. By using pairs for X we can treat, say, subtraction of integers as a function, sub:Z×Z→Z. By using pairs for Y we can draw a planar curve using a function, crv:R→R×R. On the unit interval, I, we can have a function defined to be one at rational numbers and zero otherwise, rat:I→2. By using functions for X we can consider a definite integral over the unit interval to be a function, int:[I→R]→R.
Yet we still are not satisfied. We may want even more generality, like a function whose integral is a step function; thus we define so-called generalized functions. We may want less generality, like a function we can always actually use to get a definite answer; thus we define primitive recursive functions and then limit ourselves to those we can prove are effectively computable. Or we may want to relate not just sets, but algebraic structures, complete with operations; thus we define homomorphisms.
History
The history of the function concept in mathematics is described by da Ponte (1992). As a mathematical term, "function" was coined by Gottfried Leibniz in 1694, to describe a quantity related to a curve, such as a curve's slope at a specific point. The functions Leibniz considered are today called differentiable functions. For this type of function, one can talk about limits and derivatives; both are measurements of the output or the change in the output as it depends on the input or the change in the input. Such functions are the basis of calculus.
The word function was later used by Leonhard Euler during the mid-18th century to describe an expression or formula involving various arguments, e.g. ƒ(x) = sin(x) + x3.
During the 19th century, mathematicians started to formalize all the different branches of mathematics. Weierstrass advocated building calculus on arithmetic rather than on geometry, which favoured Euler's definition over Leibniz's (see arithmetization of analysis).
At first, the idea of a function was rather limited. Joseph Fourier, for example, claimed that every function had a Fourier series, something no mathematician would claim today. By broadening the definition of functions, mathematicians were able to study "strange" mathematical objects such as continuous functions that are nowhere differentiable. These functions were first thought to be only theoretical curiosities, and they were collectively called "monsters" as late as the turn of the 20th century. However, powerful techniques from functional analysis have shown that these functions are in some sense "more common" than differentiable functions. Such functions have since been applied to the modeling of physical phenomena such as Brownian motion.
Towards the end of the 19th century, mathematicians started to formalize all of mathematics using set theory, and they sought to define every mathematical object as a set. Dirichlet and Lobachevsky are traditionally credited with independently giving the modern "formal" definition of a function as a relation in which every first element has a unique second element, but Dirichlet's claim to this formalization is disputed by Imre Lakatos:
- There is no such definition in Dirichlet's works at all. But there is ample evidence that he had no idea of this concept. In his [1837], for instance, when he discusses piecewise continuous functions, he says that at points of discontinuity the function has two values: ...
- (Proofs and Refutations, 151, Cambridge University Press 1976.)
Hardy (1908, pp. 26–28) defined a function as a relation between two variables x and y such that "to some values of x at any rate correspond values of y." He neither required the function to be defined for all values of x nor to associate each value of x to a single value of y. This broad definition of a function encompasses more relations than are ordinarily considered functions in contemporary mathematics.
The notion of a function as a rule for computing, rather than a special kind of relation, has been studied extensively in mathematical logic and theoretical computer science. Models for these computable functions include the lambda calculus, the μ-recursive functions and Turing machines.
Vocabulary
A specific input in a function is called an argument of the function. For each argument value x, the corresponding unique y in the codomain is called the function value at x, or the image of x under ƒ. The image of x may be written as ƒ(x) or as y. (See the section on notation.)
The graph of a function ƒ is the set of all ordered pairs (x, ƒ(x)), for all x in the domain X. If X and Y are subsets of R, the real numbers, then this definition coincides with the familiar sense of "graph" as a picture or plot of the function, with the ordered pairs being the Cartesian coordinates of points.
The concept of the image can be extended from the image of a point to the image of a set. If A is any subset of the domain, then ƒ(A) is the subset of the range consisting of all images of elements of A. We say the ƒ(A) is the image of A under f.
Notice that the range of ƒ is the image ƒ(X) of its domain, and that the range of ƒ is a subset of its codomain.
The preimage (or inverse image, or more precisely, complete inverse image) of a subset B of the codomain Y under a function ƒ is the subset of the domain X defined by
So, for example, the preimage of {4, 9} under the squaring function is the set {−3,−2,+2,+3}.
In general, the preimage of a singleton set (a set with exactly one element) may contain any number of elements. For example, if ƒ(x) = 7, then the preimage of {5} is the empty set but the preimage of {7} is the entire domain. Thus the preimage of an element in the codomain is a subset of the domain. The usual convention about the preimage of an element is that ƒ−1(b) means ƒ−1({b}), i.e
Three important kinds of function are the injections (or one-to-one functions), which have the property that if ƒ(a) = ƒ(b) then a must equal b; the surjections (or onto functions), which have the property that for every y in the codomain there is an x in the domain such that ƒ(x) = y; and the bijections, which are both one-to-one and onto. This nomenclature was introduced by the Bourbaki group.
When the first definition of function given above is used, since the codomain is not defined, the "surjection" must be accompanied with a statement about the set the function maps onto. For example, we might say ƒ maps onto the set of all real numbers.
Restrictions and extensions
Informally, a restriction of a function ƒ is the result of trimming its domain.
More precisely, if ƒ is a function from a X to Y, and S is any subset of X, the restriction of ƒ to S is the function ƒ|S from S to Y such that ƒ|S(s) = ƒ(s) for all s in S.
If g is any restriction of ƒ, we say that ƒ is an extension of g.
Notation
It is common to omit the parentheses around the argument when there is little chance of ambiguity, thus: sin x. In some formal settings, use of reverse Polish notation, x ƒ, eliminates the need for any parentheses; and, for example, the factorial function is always written n!, even though its generalization, the gamma function, is written Γ(n).
Formal description of a function typically involves the function's name, its domain, its codomain, and a rule of correspondence. Thus we frequently see a two-part notation, an example being
where the first part is read:
- "ƒ is a function from N to R" (one often writes informally "Let ƒ: X → Y" to mean "Let ƒ be a function from X to Y"), or
- "ƒ is a function on N into R", or
- "ƒ is a R-valued function of an N-valued variable",
and the second part is read:
 maps to
maps to 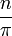
Here the function named "ƒ" has the natural numbers as domain, the real numbers as codomain, and maps n to itself divided by π. Less formally, this long form might be abbreviated
though with some loss of information; we no longer are explicitly given the domain and codomain. Even the long form here abbreviates the fact that the n on the right-hand side is silently treated as a real number using the standard embedding.
An alternative to the colon notation, convenient when functions are being composed, writes the function name above the arrow. For example, if ƒ is followed by g, where g produces the complex number eix, we may write
A more elaborate form of this is the commutative diagram.
Use of ƒ(A) to denote the image of a subset A⊆X is consistent so long as no subset of the domain is also an element of the domain. In some fields (e.g. in set theory, where ordinals are also sets of ordinals) it is convenient or even necessary to distinguish the two concepts; the customary notation is ƒ[A] for the set { ƒ(x): x ∈ A }; some authors write ƒ`x instead of ƒ(x), and ƒ``A instead of ƒ[A].
Function composition
The function composition of two or more functions uses the output of one function as the input of another. For example, ƒ(x) = sin(x2) is the composition of the sine function and the squaring function. The functions ƒ: X → Y and g: Y → Z can be composed by first applying ƒ to an argument x to obtain y = ƒ(x) and then applying g to y to obtain z = g(y). The composite function formed in this way from general ƒ and g may be written
The function on the right acts first and the function on the left acts second, reversing English reading order. We remember the order by reading the notation as "g of ƒ". The order is important, because rarely do we get the same result both ways. For example, suppose ƒ(x) = x2 and g(x) = x+1. Then g(ƒ(x)) = x2+1, while ƒ(g(x)) = (x+1)2, which is x2+2x+1, a different function.
Identity function
The unique function over a set X that maps each element to itself is called the identity function for X, and typically denoted by idX. Each set has its own identity function, so the subscript cannot be omitted unless the set can be inferred from context. Under composition, an identity function is "neutral": if ƒ is any function from X to Y, then
Inverse function
If ƒ is a function from X to Y then an inverse function for ƒ, denoted by ƒ−1, is a function in the opposite direction, from Y to X, with the property that a round trip (a composition) returns each element to itself. Not every function has an inverse; those that do are called invertible.
As a simple example, if ƒ converts a temperature in degrees Celsius to degrees Fahrenheit, the function converting degrees Fahrenheit to degrees Celsius would be a suitable ƒ−1.
The notation for composition reminds us of multiplication; in fact, sometimes we denote it using juxtaposition, gƒ, without an intervening circle. Under this analogy, identity functions are like 1, and inverse functions are like reciprocals (hence the notation).
Specifying a function
A function can be defined by any mathematical condition relating each argument to the corresponding output value. If the domain is finite, a function ƒ may be defined by simply tabulating all the arguments x and their corresponding function values ƒ(x). More commonly, a function is defined by a formula, or (more generally) an algorithm — a recipe that tells how to compute the value of ƒ(x) given any x in the domain.
There are many other ways of defining functions. Examples include recursion, algebraic or analytic closure, limits, analytic continuation, infinite series, and as solutions to integral and differential equations. The lambda calculus provides a powerful and flexible syntax for defining and combining functions of several variables.
Computability
Functions that send integers to integers, or finite strings to finite strings, can sometimes be defined by an algorithm, which gives a precise description of a set of steps for computing the output of the function from its input. Functions definable by an algorithm are called computable functions. For example, the Euclidean algorithm gives a precise process to compute the greatest common divisor of two positive integers. Many of the functions studied in the context of number theory are computable.
Fundamental results of computability theory show that there are functions that can be precisely defined but are not computable. Moreover, in the sense of cardinality, almost all functions from the integers to integers are not computable. The number of computable functions from integers to integers is countable, because the number of possible algorithms is. The number of all functions from integers to integers is higher: the same as the cardinality of the real numbers. Thus most functions from integers to integers are not computable. Specific examples of uncomputable functions are known, including the busy beaver function and functions related to the halting problem and other undecidable problems.
Functions with multiple inputs and outputs
The concept of function can be extended to an object that takes a combination of two (or more) argument values to a single result. This intuitive concept is formalized by a function whose domain is the Cartesian product of two or more sets.
For example, consider the multiplication function that associates two integers to their product: ƒ(x, y) = x·y. This function can be defined formally as having domain Z×Z , the set of all integer pairs; codomain Z; and, for graph, the set of all pairs ((x,y), x·y). Note that the first component of any such pair is itself a pair (of integers), while the second component is a single integer.
The function value of the pair (x,y) is ƒ((x,y)). However, it is customary to drop one set of parentheses and consider ƒ(x,y) a function of two variables (or with two arguments), x and y.
The concept can still further be extended by considering a function that also produces output that is expressed as several variables. For example consider the function mirror(x, y) = (y, x) with domain R×R and codomain R×R as well. The pair (y, x) is a single value in the codomain seen as a cartesian product.
Binary operations
The familiar binary operations of arithmetic, addition and multiplication, can be viewed as functions from R×R to R. This view is generalized in abstract algebra, where n-ary functions are used to model the operations of arbitrary algebraic structures. For example, an abstract group is defined as a set X and a function ƒ from X×X to X that satisfies certain properties.
Traditionally, addition and multiplication are written in the infix notation: x+y and x×y instead of +(x, y) and ×(x, y).
Function spaces
The set of all functions from a set X to a set Y is denoted by X → Y, by [X → Y], or by YX. The latter notation is justified by the fact that |YX| = |Y||X| and is an example of the convention from enumerative combinatorics that provides notations for sets based on their cardinalities.
See the article on cardinal numbers for more details.
We may interpret ƒ: X → Y to mean ƒ ∈ [X → Y]; that is, "ƒ is a function from X to Y".
Pointwise operations
If ƒ: X → R and g: X → R are functions with common domain X and common codomain a ring R, then one can define the sum function ƒ + g: X → R and the product function ƒ ⋅ g: X → R as follows:
for all x in X.
This turns the set of all such functions into a ring. The binary operations in that ring have as domain ordered pairs of functions, and as codomain functions. This is an example of climbing up in abstraction, to functions of more complex types.
By taking some other algebraic structure A in the place of R, we can turn the set of all functions from X to A into an algebraic structure of the same type in an analogous way.
Other properties
There are many other special classes of functions that are important to particular branches of mathematics, or particular applications. Here is a partial list:
- bijection, injection and surjection. You can also visit injective function, surjective function and bijective function separately.
- continuous
- differentiable, integrable
- linear, polynomial, rational
- algebraic, transcendental
- trigonometric
- fractal
- odd or even
- convex, monotonic, unimodal
- holomorphic, meromorphic, entire
- vector-valued
- computable

![\begin{align}&\scriptstyle f \colon [-1,1.5] \to [-1,1.5] \\ &\textstyle x \mapsto \frac{(4x^3-6x^2+1)\sqrt{x+1}}{3-x}\end{align}](../../images/121/12113.png)