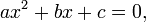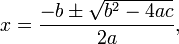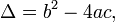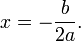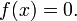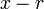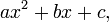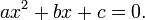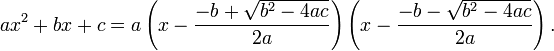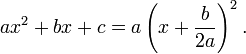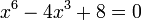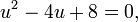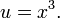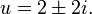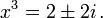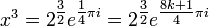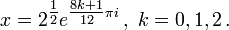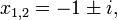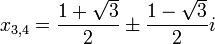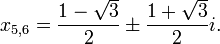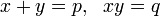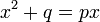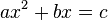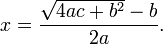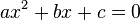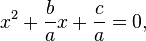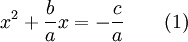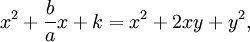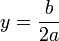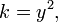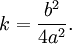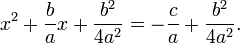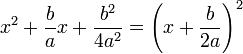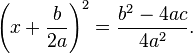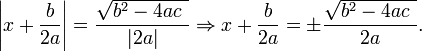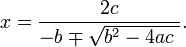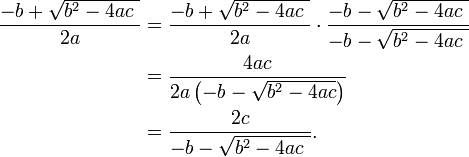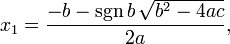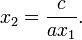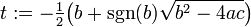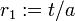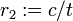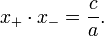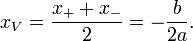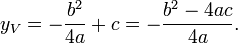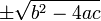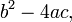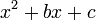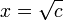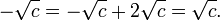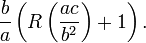Quadratic equation

Related subjects: Mathematics

Background Information

SOS Children has tried to make Wikipedia content more accessible by this schools selection. All children available for child sponsorship from SOS Children are looked after in a family home by the charity. Read more...

In mathematics, a quadratic equation is a polynomial equation of the second degree. The general form is

$ax^2+bx+c=0,\,\!$

where a ≠ 0. (For a = 0, the equation becomes a linear equation.)

The letters a, b, and c are called coefficients: the quadratic coefficient a is the coefficient of 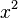$x^2$ , the linear coefficient b is the coefficient of x, and c is the constant coefficient, also called the free term or constant term.

Quadratic equations are called quadratic because quadratus is Latin for "square"; in the leading term the variable is squared.

Plots of real-valued quadratic function ax² + bx + c, varying each coefficient separately

Quadratic formula

A quadratic equation with real or complex coefficients has two (not necessarily distinct) solutions, called roots, which may be real or complex, given by the quadratic formula:

$x = \frac{-b \pm \sqrt {b^2-4ac}}{2a},$

where the symbol "±" indicates that both

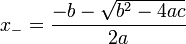
$x_+ = \frac{-b + \sqrt {b^2-4ac}}{2a}$

and

$\ x_- = \frac{-b - \sqrt {b^2-4ac}}{2a}$

are solutions.

Simply put, ± means 'plus or minus' as equation possibilities.

Discriminant

Example discriminant signs
■ <0: x²+¹⁄₂
■ =0: −⁴⁄₃x²+⁴⁄₃x−¹⁄₃
■ >0: ³⁄₂x²+¹⁄₂x−⁴⁄₃

In the above formula, the expression underneath the square root sign:

$\Delta = b^2 - 4ac , \,\!$

is called the discriminant of the quadratic equation.

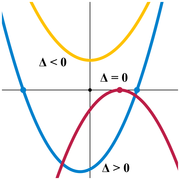
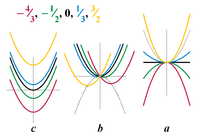
A quadratic equation with real coefficients can have either one or two distinct real roots, or two distinct complex roots. In this case the discriminant determines the number and nature of the roots. There are three cases:

If the discriminant is positive, there are two distinct roots, both of which are real numbers. For quadratic equations with integer coefficients, if the discriminant is a perfect square, then the roots are rational numbers—in other cases they may be quadratic irrationals.
If the discriminant is zero, there is exactly one distinct root, and that root is a real number. Sometimes called a double root, its value is:

$x = -\frac{b}{2a} . \,\!$
If the discriminant is negative, there are no real roots. Rather, there are two distinct (non-real) complex roots, which are complex conjugates of each other:

$\begin{align} x &= \frac{-b}{2a} + i \frac{\sqrt {4ac - b^2}}{2a} , \\ x &= \frac{-b}{2a} - i \frac{\sqrt {4ac - b^2}}{2a} , \\ i^2 &= -1. \end{align}$

Thus the roots are distinct if and only if the discriminant is non-zero, and the roots are real if and only if the discriminant is non-negative.

Geometry

For the quadratic function:
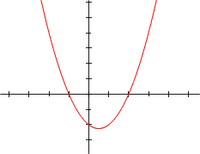
f (x) = x² − x − 2 = (x + 1)(x − 2) of a real variable x, the x- coordinates of the points where the graph intersects the x-axis, x = −1 and x = 2, are the roots of the quadratic equation: x² − x − 2 = 0.

The roots of the quadratic equation

$ax^2+bx+c=0,\,$

are also the zeros of the quadratic function:

$f(x) = ax^2+bx+c,\,$

since they are the values of x for which

$f(x) = 0.\,$

If a, b, and c are real numbers, and the domain of f is the set of real numbers, then the zeros of f are exactly the x- coordinates of the points where the graph touches the x-axis.

It follows from the above that, if the discriminant is positive, the graph touches the x-axis at two points, if zero, the graph touches at one point, and if negative, the graph does not touch the x-axis.

Quadratic factorization

The term

$x - r\,$

is a factor of the polynomial

$ax^2+bx+c, \$

if and only if r is a root of the quadratic equation

$ax^2+bx+c=0. \$

It follows from the quadratic formula that

$ax^2+bx+c = a \left( x - \frac{-b + \sqrt {b^2-4ac}}{2a} \right) \left( x - \frac{-b - \sqrt {b^2-4ac}}{2a} \right).$

In the special case where the quadratic has only one distinct root (i.e. the discriminant is zero), the quadratic polynomial can be factored as

$ax^2+bx+c = a \left( x + \frac{b}{2a} \right)^2.\,\!$

Application to higher-degree equations

Certain higher-degree equations can be brought into quadratic form and solved that way. For example, the 6th-degree equation in x:

$x^6 - 4x^3 + 8 = 0\,$

can be rewritten as:

$(x^3)^2 - 4(x^3) + 8 = 0\,,$

or, equivalently, as a quadratic equation in a new variable u:

$u^2 - 4u + 8 = 0,\,$

where

$u = x^3.\,$

Solving the quadratic equation for u results in the two solutions:

$u = 2 \pm 2i.$

Thus

$x^3 = 2 \pm 2i\,.$

Concentrating on finding the three cube roots of

– the other three solutions for x will be their complex conjugates – rewriting the right-hand side using Euler's formula:

$x^3 = 2^{\tfrac{3}{2}}e^{\tfrac{1}{4}\pi i} = 2^{\tfrac{3}{2}}e^{\tfrac{8k+1}{4}\pi i}\,$

(since e^2kπi = 1), gives the three solutions:

$x = 2^{\tfrac{1}{2}}e^{\tfrac{8k+1}{12}\pi i}\,,~k = 0, 1, 2\,.$

Using Eulers' formula again together with trigonometric identities such as cos(π/12) =

, and adding the complex conjugates, gives the complete collection of solutions as:

$x_{1,2} = -1 \pm i,\,$

$x_{3,4} = \frac{1 + \sqrt{3}}{2} \pm \frac{1 - \sqrt{3}}{2}i\,$

and

$x_{5,6} = \frac{1 - \sqrt{3}}{2} \pm \frac{1 + \sqrt{3}}{2}i.\,$

History

The Babylonians, as early as 1800 BC (displayed on Old Babylonian clay tablets) could solve a pair of simultaneous equations of the form:

$x+y=p,\ \ xy=q \$

which are equivalent to the equation:

$\ x^2+q=px$

The original pair of equations were solved as follows:

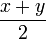
Form $\frac{x+y}{2}$
Form $\left(\frac{x+y}{2}\right)^2$
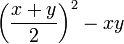
Form $\left(\frac{x+y}{2}\right)^2 - xy$
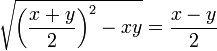
Form $\sqrt{\left(\frac{x+y}{2}\right)^2 - xy} = \frac{x-y}{2}$
Find $x,\ y$ by inspection of the values in (1) and (4).

In the Sulba Sutras in ancient India circa 8th century BCE quadratic equations of the form ax² = c and ax² + bx = c were explored using geometric methods. Babylonian mathematicians from circa 400 BCE and Chinese mathematicians from circa 200 BCE used the method of completing the square to solve quadratic equations with positive roots, but did not have a general formula. Euclid, the Greek mathematician, produced a more abstract geometrical method around 300 BCE.

In 628 CE, Brahmagupta gave the first explicit (although still not completely general) solution of the quadratic equation:

$\ ax^2+bx=c$

“

To the absolute number multiplied by four times the [coefficient of the] square, add the square of the [coefficient of the] middle term; the square root of the same, less the [coefficient of the] middle term, being divided by twice the [coefficient of the] square is the value. (Brahmasphutasiddhanta (Colebrook translation, 1817, page 346)

”

This is equivalent to:

$x = \frac{\sqrt{4ac+b^2}-b}{2a}.$

The Bakhshali Manuscript dated to have been written in India in the 7th century CE contained an algebraic formula for solving quadratic equations, as well as quadratic indeterminate equations (originally of type ax/c = y). Mohammad bin Musa Al-kwarismi (Persia, 9th century) developed a set of formulae that worked for positive solutions. His work was based on Brahmagupta. Abraham bar Hiyya Ha-Nasi (also known by the Latin name Savasorda) introduced the complete solution to Europe in his book Liber embadorum in the 12th century. Bhāskara II ( 1114– 1185), an Indian mathematician– astronomer, gave the first general solution to the quadratic equation with two roots.

The writing of the Chinese mathematician Yang Hui ( 1238- 1298 AD) represents the first in which quadratic equations with negative coefficients of 'x' appear, although he attributes this to the earlier Liu Yi.

Derivation

The quadratic formula can be derived by the method of completing the square, so as to make use of the algebraic identity:

$x^2+2xy+y^2 = (x+y)^2.\,\!$

Dividing the quadratic equation

$ax^2+bx+c=0 \,\!$

by a (which is allowed because a is non-zero), gives:

$x^2 + \frac{b}{a} x + \frac{c}{a}=0,\,\!$

$x^2 + \frac{b}{a} x= -\frac{c}{a} \qquad (1)$

The quadratic equation is now in a form in which the method of completing the square can be applied. To "complete the square" is to find some constant k such that

$x^2 + \frac{b}{a}x + k = x^2+2xy+y^2,\,\!$

for another constant y. In order for these equations to be true,

$\frac{b}{a} = 2y\!$

$y = \frac{b}{2a}\,\!$

and

$k = y^2,\,\!$

thus

$k = \frac{b^2}{4a^2}.\,\!$

Adding this constant to equation (1) produces

$x^2+\frac{b}{a}x+\frac{b^2}{4a^2}=-\frac{c}{a}+\frac{b^2}{4a^2}.\,\!$

The left side is now a perfect square because

$x^2+\frac{b}{a}x+\frac{b^2}{4a^2} = \left( x + \frac{b}{2a} \right)^2$

The right side can be written as a single fraction, with common denominator 4a². This gives

$\left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}.$

Taking the square root of both sides yields

$\left|x+\frac{b}{2a}\right| = \frac{\sqrt{b^2-4ac\ }}{|2a|}\Rightarrow x+\frac{b}{2a}=\pm\frac{\sqrt{b^2-4ac\ }}{2a}.$

Isolating x, gives

$x=-\frac{b}{2a}\pm\frac{\sqrt{b^2-4ac\ }}{2a}=\frac{-b\pm\sqrt{b^2-4ac\ }}{2a}.$

Alternative formula

In some situations it is preferable to express the roots in an alternate form.

$x =\frac{2c}{-b \mp \sqrt {b^2-4ac\ }} .$

This alternative requires c to be nonzero; for, if c is zero, the formula correctly gives zero as one root, but fails to give any second, non-zero root. Instead, one of the two choices for ∓ produces a division by zero, which is undefined.

The roots are the same regardless of which expression we use; the alternate form is merely an algebraic variation of the common form:

$\begin{align} \frac{-b + \sqrt {b^2-4ac\ }}{2a} &{}= \frac{-b + \sqrt {b^2-4ac\ }}{2a} \cdot \frac{-b - \sqrt {b^2-4ac\ }}{-b - \sqrt {b^2-4ac\ }} \\ &{}= \frac{4ac}{2a \left ( -b - \sqrt {b^2-4ac} \right ) } \\ &{}=\frac{2c}{-b - \sqrt {b^2-4ac\ }}. \end{align}$

The alternative formula can reduce loss of precision in the numerical evaluation of the roots, which may be a problem if one of the roots is much smaller than the other in absolute magnitude. The problem of c possibly being zero can be avoided by using a mixed approach:

$x_1 = \frac{-b - \sgn b \,\sqrt {b^2-4ac}}{2a},$

$x_2 = \frac{c}{ax_1}.$

Here sgn denotes the sign function.

Floating point implementation

A careful floating point computer implementation differs a little from both forms to produce a robust result. Assuming the discriminant, b²−4ac, is positive and b is nonzero, the code will be something like the following.

$t := -\tfrac12 \big( b + \sgn(b) \sqrt{b^2-4ac} \big) \,\!$

$r_{1} := t/a \,\!$

$r_{2} := c/t \,\!$

Here sgn(b) is the sign function, where sgn(b) is 1 if b is positive and −1 if b is negative; its use ensures that the quantities added are of the same sign, avoiding catastrophic cancellation. The computation of r₂ uses the fact that the product of the roots is c/a.

Viète's formulas

Viète's formulas give a simple relation between the roots of a polynomial and its coefficients. In the case of the quadratic polynomial, they take the following form:

$x_+ + x_- = -\frac{b}{a}$

and

$x_+ \cdot x_- = \frac{c}{a}.$

The first formula above yields a convenient expression when graphing a quadratic function. Since the graph is symmetric with respect to a vertical line through the vertex, when there are two real roots the vertex’s x-coordinate is located at the average of the roots (or intercepts). Thus the x-coordinate of the vertex is given by the expression:

$x_V = \frac {x_+ + x_-} {2} = -\frac{b}{2a}.$

The y-coordinate can be obtained by substituting the above result into the given quadratic equation, giving

$y_V = - \frac{b^2}{4a} + c = - \frac{ b^2 - 4ac} {4a}.$

Generalizations

The formula and its derivation remain correct if the coefficients a, b and c are complex numbers, or more generally members of any field whose characteristic is not 2. (In a field of characteristic 2, the element 2a is zero and it is impossible to divide by it.)

The symbol

$\pm \sqrt {b^2-4ac}$

in the formula should be understood as "either of the two elements whose square is

$b^2-4ac,\,$

if such elements exist. In some fields, some elements have no square roots and some have two; only zero has just one square root, except in fields of characteristic 2. Note that even if a field does not contain a square root of some number, there is always a quadratic extension field which does, so the quadratic formula will always make sense as a formula in that extension field.

Characteristic 2

In a field of characteristic 2, the quadratic formula, which relies on 2 being a unit, does not hold. Consider the monic quadratic polynomial

$\displaystyle x^{2} + bx + c$

over a field of characteristic 2. If b = 0, then the solution reduces to extracting a square root, so the solution is

$\displaystyle x = \sqrt{c}$

and note that there is only one root since

$\displaystyle -\sqrt{c} = -\sqrt{c} + 2\sqrt{c} = \sqrt{c}.$

In summary,

$\displaystyle x^{2} + c = (x + \sqrt{c})^{2}.$

See quadratic residue for more information about extracting square roots in finite fields.

In the case that b ≠ 0, there are two distinct roots, but if the polynomial is irreducible, they cannot be expressed in terms of square roots of numbers in the coefficient field. Instead, define the 2-root R(c) of c to be a root of the polynomial x² + x + c, an element of the splitting field of that polynomial. One verifies that R(c) + 1 is also a root. In terms of the 2-root operation, the two roots of the (non-monic) quadratic ax² + bx + c are

$\frac{b}{a}R\left(\frac{ac}{b^2}\right)$

and

$\frac{b}{a}\left(R\left(\frac{ac}{b^2}\right)+1\right).$

For example, let a denote a multiplicative generator of the group of units of F₄, the Galois field of order four (thus a and a + 1 are roots of x² + x + 1 over F₄). Because (a + 1)² = a, a + 1 is the unique solution of the quadratic equation x² + a = 0. On the other hand, the polynomial x + ax + 1 is irreducible over F₄, but splits over F₁₆, where it has the two roots ab and ab + a, where b is a root of x² + x + a in F₁₆.

This is a special case of Artin-Schreier theory.

Book

Vedic Mathematics: Sixteen Simple Mathematical Formulae from the Vedas, by Swami Sankaracarya (1884-1960), Motilal Banarsidass Indological Publishers and Booksellers, Varnasi, India, 1965; reprinted in Delhi, India, 1975, 1978. 367 pages.

Retrieved from " http://en.wikipedia.org/w/index.php?title=Quadratic_equation&oldid=199164119"