Divisor
Background to the schools Wikipedia
Arranging a Wikipedia selection for schools in the developing world without internet was an initiative by SOS Children. Before you decide about sponsoring a child, why not learn about different sponsorship charities first?
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which evenly divides n without leaving a remainder.
Explanation
For example, 7 is a divisor of 42 because 42/7 = 6. We also say 42 is divisible by 7 or 42 is a multiple of 7 or 7 divides 42 or 7 is a factor of 42 and we usually write 7 | 42. For example, the positive divisors of 42 are 1, 2, 3, 6, 7, 14, 21, 42.
In general, we say m|n (read: m divides n) for non-zero integers m and n iff there exists an integer k such that n = km. Thus, divisors can be negative as well as positive, although often we restrict our attention to positive divisors. (For example, there are six divisors of four, 1, 2, 4, −1, −2, −4, but one would usually mention only the positive ones, 1, 2, and 4.)
1 and −1 divide (are divisors of) every integer, every integer (and its negation) is a divisor of itself, and every integer is a divisor of 0, except by convention 0 itself (see also division by zero). Numbers divisible by 2 are called even and numbers not divisible by 2 are called odd.
A divisor of n that is not 1, −1, n or −n (which are trivial divisors) is known as a non-trivial divisor; numbers with non-trivial divisors are known as composite numbers, while prime numbers have no non-trivial divisors.
The name comes from the arithmetic operation of division: if a/b = c then a is the dividend, b the divisor, and c the quotient.
There are properties which allow one to recognize certain divisors of a number from the number's digits.
Further notions and facts
| The Wikibook The Book of Mathematical Proofs has a page on the topic of: Proofs of properties of divisibility |
Some elementary rules:
- If a | b and a | c, then a | (b + c), in fact, a | (mb + nc) for all integers m, n.
- If a | b and b | c, then a | c. ( transitive relation)
- If a | b and b | a, then a = b or a = −b.
The following property is important:
- If a | bc, and gcd(a,b) = 1, then a | c. ( Euclid's lemma)
A positive divisor of n which is different from n is called a proper divisor (or aliquot part) of n. (A number which does not evenly divide n, but leaves a remainder, is called an aliquant part of n.)
An integer n > 1 whose only proper divisor is 1 is called a prime number. Equivalently, one would say that a prime number is one which has exactly two factors: 1 and itself.
Any positive divisor of n is a product of prime divisors of n raised to some power. This is a consequence of the Fundamental theorem of arithmetic.
If a number equals the sum of its proper divisors, it is said to be a perfect number. Numbers less than the sum of their proper divisors are said to be abundant; while numbers greater than that sum are said to be deficient.
The total number of positive divisors of n is a multiplicative function d(n) (e.g. d(42) = 8 = 2×2×2 = d(2)×d(3)×d(7)). The sum of the positive divisors of n is another multiplicative function σ(n) (e.g. σ(42) = 96 = 3×4×8 = σ(2)×σ(3)×σ(7)). Both of these functions are examples of divisor functions.
If the prime factorization of n is given by
then the number of positive divisors of n is
and each of the divisors has the form
where  for each
for each 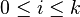 .
.
One can show that
One interpretation of this result is that a randomly chosen positive integer n has an expected number of divisors of about  .
.
Divisibility of numbers
The relation of divisibility turns the set N of non-negative integers into a partially ordered set, in fact into a complete distributive lattice. The largest element of this lattice is 0 and the smallest one is 1. The meet operation ^ is given by the greatest common divisor and the join operation v by the least common multiple. This lattice is isomorphic to the dual of the lattice of subgroups of the infinite cyclic group Z.
Generalization
One can talk about the concept of divisibility in any integral domain. Please see that article for the definitions in that setting.