Chapter 4
Functions
By Boundless
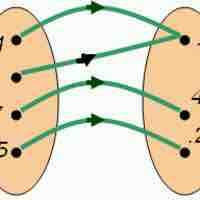
A function maps a set of inputs onto a set of permissible outputs. Each input corresponds with one and only one output
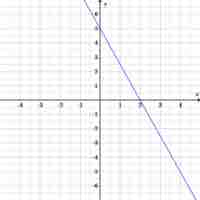
Graphs are a great visual representation of functions, showing the relationship between the input and output values as lines or curves
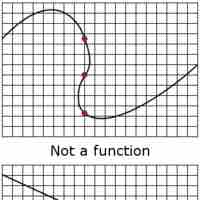
The vertical line test is used to determine whether a curve on an
The domain of a function is the set of all possible input values that produce some output value range
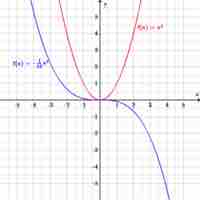
All values in the domain are mapped onto values in the range that are visualized as graphs of functions
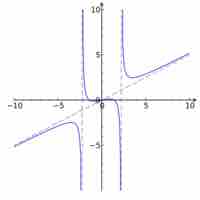
Rational and radical expressions have restrictions on their domains which can be found algebraically or graphically.
Functions can either be constant, increasing as
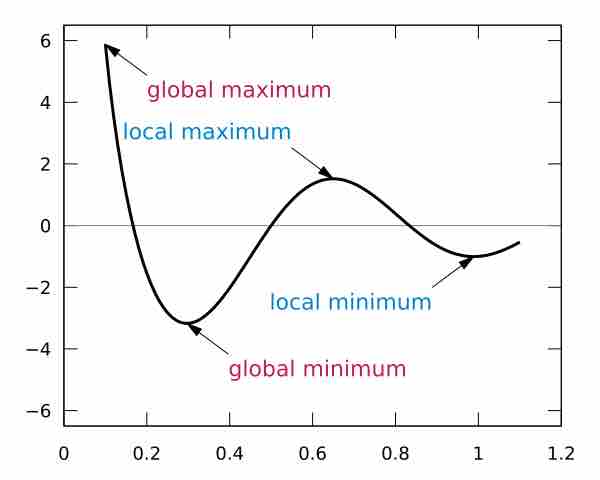
Relative minima and maxima are points of the smallest and greatest values in their neighborhoods respectively.
A piecewise function is defined by multiple subfunctions that are each applied to separate intervals of the input
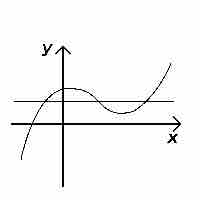
A one-to-one function, also called an injective function, never maps distinct elements of its domain to the same element of its codomain.
Two objects have symmetry if one object can be obtained from the other by a transformation.
Functions that have an additive inverse can be classified as odd or even depending on their symmetry properties.

Transformations alter a function while maintaining the original characteristics of that function.

A translation of a function is a shift in one or more directions. It is represented by adding or subtracting from either y or x.

Reflections are a type of transformation that move an entire curve such that its mirror image lies on the other side of the
Stretching and shrinking refer to transformations that alter how compact a function looks in the