A translation moves every point in a function a constant distance in a specified direction. In algebra, this essentially manifests as a vertical or horizontal shift of a function. A translation can be interpreted as shifting the origin of the coordinate system.
Vertical Translations
To translate a function vertically is to shift the function up or down. If a positive number is added, the function shifts up the
where
Let's use a basic quadratic function to explore vertical translations. The original function we will use is:
Translating the function up the
And translating the function down the
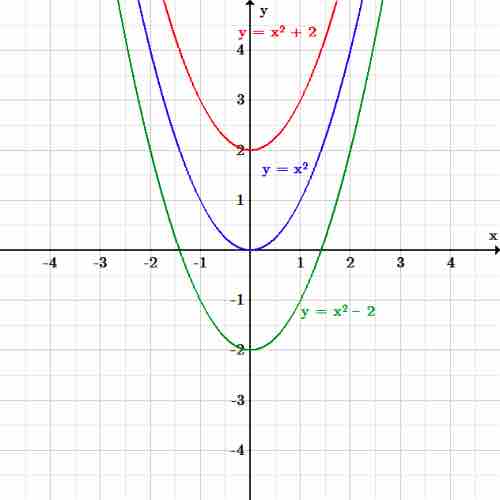
Vertical translations
The function
Horizontal Translations
To translate a function horizontally is the shift the function left or right. While vertical shifts are caused by adding or subtracting a value outside of the function parameters, horizontal shifts are caused by adding or subtracting a value inside the function parameters. The general equation for a horizontal shift is given by:
Where
Let's use the same basic quadratic function to look at horizontal translations. Again, the original function is:
Shifting the function to the left by two produces the equation:
Shifting the function to the right by two produces the equation:
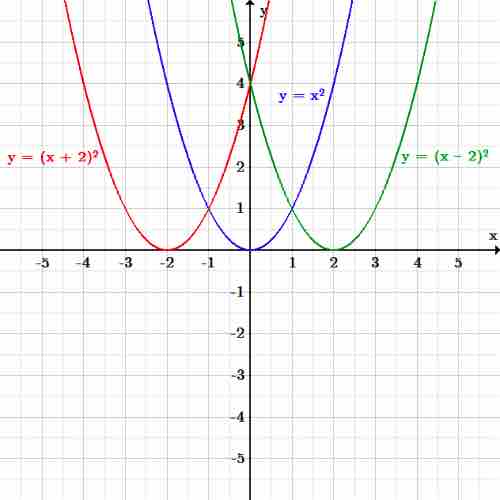
Horizontal translation
The function