Graphical Behavior of Functions

As part of exploring how functions change, we can identify intervals over which the function is changing in specific ways. We say that a function is increasing on an interval if the function values increase as the input values increase within that interval. Similarly, a function is decreasing on an interval if the function values decrease as the input values increase over that interval.

• An increasing function is one where for every $x_1$ and $x_2$ that satisfies $x_2 > x_1$, then $f(x_{2}) \geq f(x_{1})$. If it is strictly greater than $(f(x_2)>f(x_1))$, then it is strictly increasing.
• A decreasing function is one where for every $x_1$and $x_2$ that satisfies $x_2 > x_1$, then $f(x_{2}) \leq f(x_{1})$. If it is strictly less than $(f(x_2) < f(x_1))$, then it is strictly decreasing.

In terms of a linear function $f(x)=mx+b$, if $m$ is positive, the function is increasing, if $m$ is negative, it is decreasing, and if $m$ is zero, the function is a constant function.

The average rate of change of an increasing function is positive, and the average rate of change of a decreasing function is negative. The figure below shows examples of increasing and decreasing intervals on a function.

Types of Functions

The function $f(x)=x^3−12x$ is increasing on the $x$-axis from negative infinity to $-2$ and also from $2$ to positive infinity.  The interval notation is written as: $(−∞, −2)∪(2, ∞)$.  The function is decreasing on on the interval: $ (−2, 2)$.  

Constant Functions

In mathematics, a constant function is a function whose values do not vary, regardless of the input into the function.  A function is a constant function if $f(x)=c$ for all values of $x$ and some constant $c$.  The graph of the constant function $y(x)=c$ is a horizontal line in the plane that passes through the point $(0,c).$

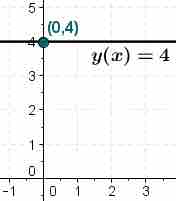
Constant Function

The graph of $f(x)=4 $ illustrates a constant function. 

Identifying Function Behavior

Example 1:  Identify the intervals where the function is increasing, decreasing, or constant.

Look at the graph from left to right on the $x$-axis; the first part of the curve is decreasing from infinity to the $x$-value of $-1$ and then the curve increases.  The curve increases on the interval from $-1$ to $1$ and then it decreases again to infinity. There are no intervals where this curve is constant.

Increasing Decreasing Function Graph

For the function pictured above, the curve is decreasing across the intervals:   $(-\infty,-1)\cup (1,\infty )$ and increasing on the interval $ (-1,1)$.