Finding Domains of Rational Functions

A rational expression is one which can be written as the ratio of two polynomial functions. Despite being called a rational expression, neither the coefficients of the polynomials nor the values taken by the function are necessarily rational numbers. In the case of one variable, $x$, an expression is called rational if and only if it can be written in the form:

$\displaystyle \frac { P(x) }{ Q(x) }$

where $P(x)$ and $Q(x)$ are polynomial functions in $x $ and $Q(x)$ is not the zero polynomial $(Q(x) \neq 0)$.

The domain of a rational expression of is the set of all points for which the denominator is not zero. If the denominator of the equation becomes equal to zero, the expression is undefined at that point.

Example 1:  What is the domain of the rational function:

 $\displaystyle f(x)= \frac { x^3-2x }{ 2(x^2-5) }$

To find the domain of a rational function, set the denominator equal to zero and solve.  All values of $x$ except for those that satisfy $2(x^2-5)=0$ are the domain of the expression.  

$\displaystyle 2(x^2-5)=0$

To solve, divide both sides by $2$, add $5$ to both sides, and then take the square root of both sides to yield:

$\displaystyle x=\pm \sqrt { 5 }$.  

Therefore the domain is the set of all real numbers except the square root of five or negative square root of five.

Notice the graph of the function below.  At the values of $x=\pm \sqrt { 5 }$ (which is approximately $\pm 2.2$), the graph does not exist.

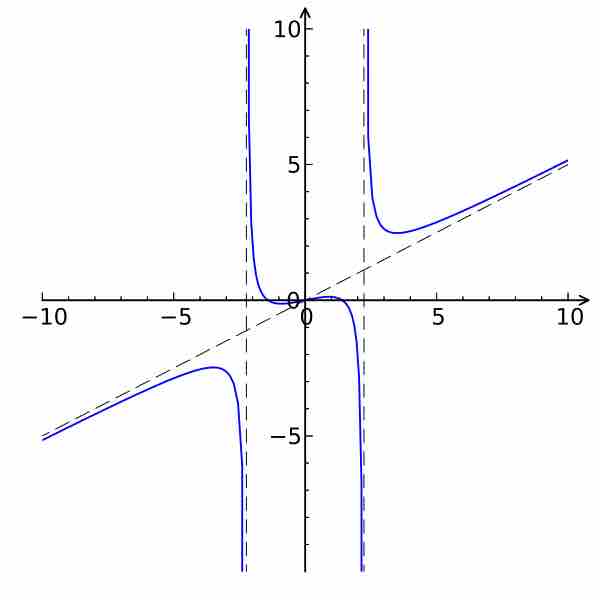
Rational function with restricted domain

The graph of the function: $f(x)=\displaystyle \frac { x^3-2x }{ 2(x^2-5) }$, where the domain is restricted at $x=\pm \sqrt { 5 }$ since the function does not exist at those points.

Example 2:  What is the domain of the rational function: 

$\displaystyle f(x)= \frac{\left(x^2-2\right)}{x}$ 

Algebraically, the domain is the set of all real numbers except zero, since the denominator can not equal zero. One way to determine this is to look at it graphically. We can see that the graph is discontinuous at $x=0$, indicating that the domain is all numbers other than $x=0$. This makes sense, because at $x=0$ we would have to divide by zero, which is undefined.  The red lines of the graph get closer and closer to the value $x=0$, but never touch.

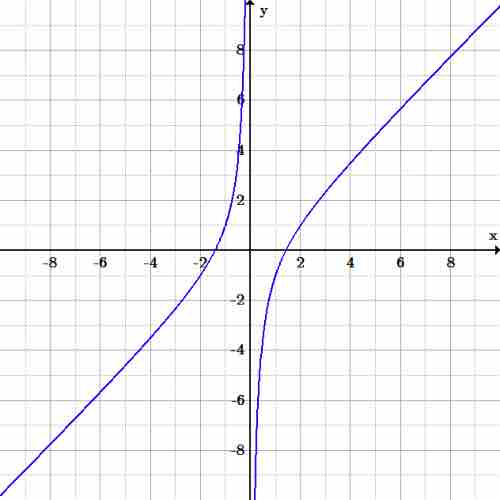
Rational Function Dividing by $x$

A graph of the equation: $f(x)= \frac{\left(x^2-2\right)}{x}$ . To determine the domain of this function, we can graph it and look for where the function doesn't exist, in this case when $x=0$.

Finding Domains of Radical Functions

The principal square root function $f(x)=\sqrt x$ (usually just referred to as the "square root function") is a function that maps the set of non-negative real numbers onto itself.  

Radical Function

The function $f(x)=\sqrt x$ consists of a restricted domain of $x\geq 0$, or non-negative real numbers, since we can not take the square root of a negative number.  

Note that half of the parabola is missing since functions cannot have more than one value at a point, and the square root function is taken to yield a positive value (though $(-x)^2$ gives the same value as $x^2$ so the square root of a number $y$ such that $y=x^2$ would be $\sqrt y = \pm x$). It is important to remember when graphing the roots that negative values of $x$ will not produce real numbers. This will be explained further in the section on imaginary numbers.

To determine the domain of a radical function algebraically, find the values of $x$ for which the radicand is nonnegative (set it equal to $\geq 0$) and then solve for $x$.  The radicand is the number or expression underneath the radical sign.  All values of $x$ except for those that satisfy $\sqrt x \geq 0$ are the domain of the function. 

Example 3:  What is the domain of the radical function:

 $\displaystyle f(x) = \sqrt {x-3} +4$

Set the radicand greater than or equal to zero and solve for $x$ to find the restrictions on the domain:

 $\displaystyle {x-3} \geq 0$

Therefore $x \geq 3$.  So, all real number greater than or equal to $3$ is the domain of the function.

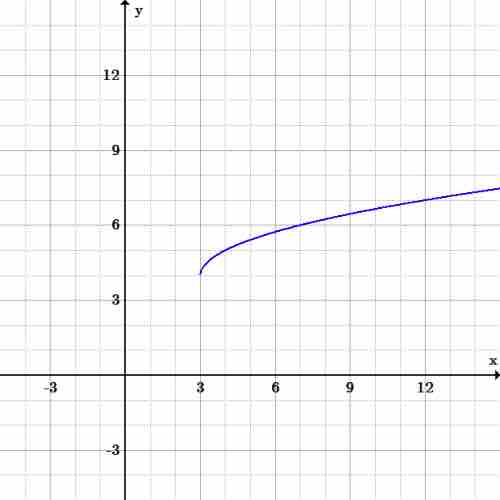
Radical function

The graph of the equation: $f(x) = \sqrt {x-3} +4$.  The function has the domain of all real numbers greater than or equal to $3$, as shown in the graph above.