Even and Odd Definitions

Functions can be classified as "odd" or "even" based on their composition. These labels correlate with symmetry properties of the function.

The terms "odd" and "even" can only be applied to a limited set of functions. For a function to be classified as one or the other, it must have an additive inverse. Therefore, it must have a number that, when added to it, equals $0$.

Oftentimes, the parity of a function will reveal whether it is odd or even. For example, the function $f(x)=x^2$ is even because it has an exponent, $2$, that is an even integer. This, however, does not apply in every instance.  For example, $f(x)=\left | x^3 \right |$ has an exponent that is of an odd integer, $3$, but is also an even function.  How can we check if a function is odd or even?  Let's look at their characteristics.

Even Functions

Even functions are algebraically defined as functions in which the following relationship holds for all values of $x$:

$\displaystyle f(x)=f(-x)$

To check if a function is even, any $x$-value chosen must yield the same output value when substituted into the function as $-x$.  

Example 1: Is the function $f(x)=x^4+2x$ even?  

Remember the degree of the function, in this case a $4$ which is even, may not always dictate if the function is in fact even.  

First, perform an algebraic check:  Substitute a value for $x$ and $-x$ into the function and check that the same output is found.  Let $x=2$: will $f(2)=f(-2)?$

$\displaystyle \begin{aligned} f(2)&=(2)^4+2(2)\\ &=16+4\\ &=20 \end{aligned}$         

$\displaystyle \begin{aligned} f(-2)&=(-2)^4+2(-2)\\ &=16-4\\ &=12 \end{aligned}$

Therefore $f(2)\neq f(-2)$ and the function is not even.

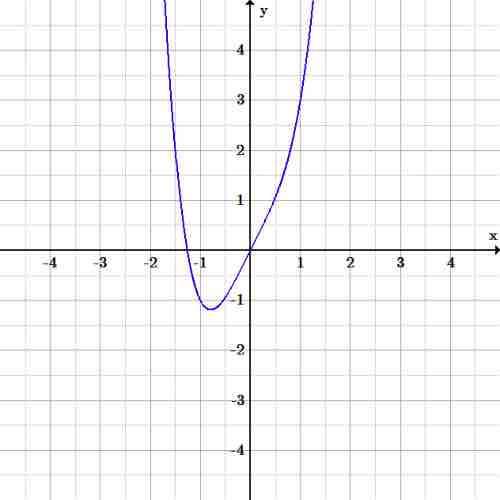
Symmetry: even function?

The function $f(x)=x^4+2x$ pictured above is not even because the graph is not symmetric about the $y$-axis.  For example the point $(-1,-1)$ does not reflect onto the point $(1,-1)$.  

We can confirm this graphically: functions that satisfy the requirements of being even are symmetric about the $y$-axis. Therefore, for every point $(x,y)$ on the graph, the corresponding point $(-x,y)$ or vice versa, is also on the graph.  

Odd Functions

Odd functions are algebraically defined as functions in which the following relationship holds true for all values of $x$:

$\displaystyle -f(x)=f(-x)$

This relationship can also be expressed as:

$\displaystyle f(x)+f(-x)=0$

To check if a function is odd, the negation of the function (be sure to negate all terms of the function) must yield the same output as substituting the value $-x$.

Example 2: Is the function $f(x)=x^3-9x$ odd?

Algebraic check: Does $-f(x)=f(-x)$?  

$\displaystyle \begin{aligned} -f(x)&=-(x^3-9x)\\& =-x^3+9x \end{aligned}$

$\displaystyle \begin{aligned} f(-x)&=(-x)^3-9(-x)\\& =-x^3+9x \end{aligned}$

Therefore $-f(x)=f(-x)$ and the function is odd.

Graphical check:  Functions that satisfy the requirements of being odd are symmetric with respect to the origin. In other words, rotating the graph $180$ degrees about the point of origin results in the same, unchanged graph.  In addition, for every point $(x,y)$ on the graph, the corresponding point $(-x,-y)$ is also on the graph. 

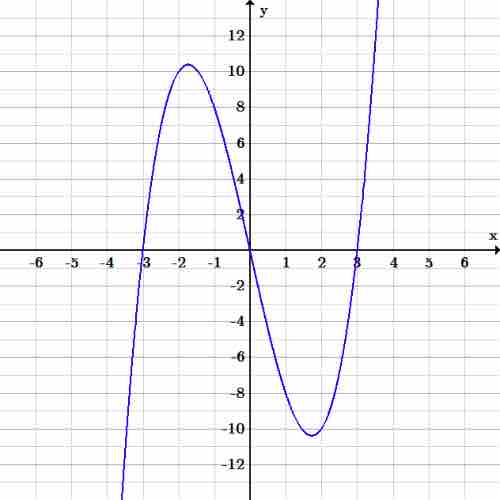
Symmetry: odd function?

The function, $f(x)=x^3-9x$ is odd since the graph is symmetric about the origin.  One can also check that any point is symmetric about the origin: for example, does $(-1,8)$ yield $(1,-8)$?  Yes, those two points are symmetric about the origin.