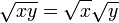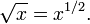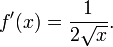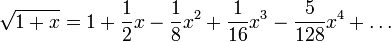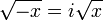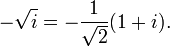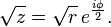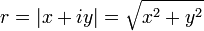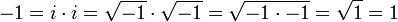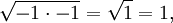Square root
Background Information
This Schools selection was originally chosen by SOS Children for schools in the developing world without internet access. It is available as a intranet download. All children available for child sponsorship from SOS Children are looked after in a family home by the charity. Read more...
In mathematics, a square root (√) of a number x is a number r such that r2 = x, or in words, a number r whose square (the result of multiplying the number by itself) is x. Every non-negative real number x has a unique non-negative square root, called the principal square root and denoted with a radical symbol as √x. For example, the principal square root of 9 is 3, denoted √9 = 3, because 32 = 3 × 3 = 9.
Square roots often arise when solving quadratic equations, or equations of the form ax2 + bx + c = 0, due to the variable x being squared.
Every positive number x has two square roots. One of them is √x, which is positive, and the other −√x, which is negative. Together, these two roots are denoted ±√x. Square roots of negative numbers can be discussed within the framework of complex numbers. Square roots of objects other than numbers can also be defined.
Square roots of integers that are not perfect squares are always irrational numbers: numbers not expressible as a ratio of two integers. For example, √2 cannot be written exactly as m/n, where n and m are integers. Nonetheless, it is exactly the length of the diagonal of a square with side length 1. This has been known since ancient times, with the discovery that √2 is irrational attributed to Hipparchus, a disciple of Pythagoras. (See square root of 2 for proofs of the irrationality of this number.)
Properties
The principal square root function f(x) = √x (usually just referred to as the "square root function") is a function which maps the set of non-negative real numbers R+ ∪ {0} onto itself, and, like all functions, always returns a unique value. The square root function also maps rational numbers into algebraic numbers (a superset of the rational numbers); √x is rational if and only if x is a rational number which can be represented as a ratio of two perfect squares. In geometrical terms, the square root function maps the area of a square to its side length.
- For all real numbers x,
-
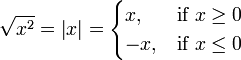 (see absolute value)
(see absolute value)
- For all non-negative real numbers x and y,
-
- and
- The square root function is continuous for all non-negative x and differentiable for all positive x. Its derivative is given by
- The Taylor series of √1 + x about x = 0 converges for | x | < 1 and is given by
Computation
Many methods of calculating square roots exist today, some meant to be done by hand and some meant to be done by machine.
Many, but not all pocket calculators have a square root key. Computer spreadsheets and other software are also frequently used to calculate square roots. Computer software programs typically implement good routines to compute the exponential function and the natural logarithm or logarithm, and then compute the square root of x using the identity
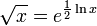 or
or 
The same identity is exploited when computing square roots with logarithm tables or slide rules.
The most common method of square root calculation by hand is known as the " Babylonian method". It involves a simple algorithm, which results in a number closer to the actual square root each time it is repeated. To find r, the square root of a real number x:
- Start with an arbitrary positive start value r (the closer to the square root of x, the better).
- Replace r by the average between r and x/r. (It is sufficient to take an approximate value of the average, not too close to the previous value of r and x/r in order to ensure convergence.)
- Repeat step 2 until r and x/r are as close as desired.
The best known time complexity for computing a square root with n digits of precision is the same as that for multiplying two n-digit numbers.
Square roots of negative and complex numbers
The square of any positive or negative number is positive, and the square of 0 is 0. Therefore, no negative number can have a real square root. However, it is possible to work with a larger set of numbers, called the complex numbers, that does contain solutions to the square root of a negative number. This is done by introducing a new number, denoted by i (sometimes j, especially in the context of electricity) and called the imaginary unit, which is defined such that i2 = −1. Using this notation, we can think of i as the square root of −1, but notice that we also have (−i)2 = i2 = −1 and so −i is also a square root of −1. Similarly to the real numbers, we say the principal square root of −1 is i, or more generally, if x is any positive number, then the principal square root of −x is
because
By the argument given above, i can be neither positive nor negative. This creates a problem: for the complex number z, we cannot define √z to be the "positive" square root of z.
For every non-zero complex number z there exist precisely two numbers w such that w2 = z. For example, the square roots of i are:
and
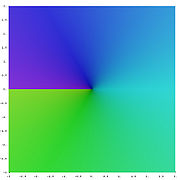
The usual definition of √z is by introducing the following branch cut: if z = r eiφ is represented in polar coordinates with −π < φ ≤ π, then we set the principal value to
Thus defined, the square root function is holomorphic everywhere except on the non-positive real numbers (where it isn't even continuous). The above Taylor series for √1 + x remains valid for complex numbers x with | x | < 1.
When the number is in rectangular form the following formula can be used for the principal value:
where
is the absolute value or modulus of the complex number, unless x = −r and y = 0. Notice that the sign of the imaginary part of the root is the same as the sign of the imaginary part of the original number. The real part of the principal value is always non-negative.
Note that because of the discontinuous nature of the square root function in the complex plane, the law √zw = √z√w is in general not true. (Equivalently, the problem occurs because of the freedom in the choice of branch. The chosen branch may or may not yield the equality; in fact, the choice of branch for the square root need not contain the value of √z√w at all, leading to equality's failure. A similar problem appears with the complex logarithm and the relation log z + log w = log(zw).) Wrongly assuming this law underlies several faulty "proofs", for instance the following one showing that −1 = 1:
The third equality cannot be justified (see invalid proof), however, it can be adjusted to be true if we (1) permit freedom in the choice of branch by no longer requiring the principal square root (defined in the beginning of the article) implicit in the √ notation and (2) choose the square root's branch so as to exclude the value 1. The left hand side becomes either
if the branch includes +i or
if the branch includes −i, while the right hand side becomes
again by the choice of branch.
Square roots of matrices and operators
If A is a positive-definite matrix or operator, then there exists precisely one positive definite matrix or operator B with B2 = A; we then define √A = B.
More generally, to every normal matrix or operator A there exist normal operators B such that B2 = A. In general, there are several such operators B for every A and the square root function cannot be defined for normal operators in a satisfactory manner. Positive definite operators are akin to positive real numbers, and normal operators are akin to complex numbers.
Principal square roots of the first 20 positive integers
As non-periodic decimal fractions
-
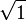

1 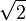
1.4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462 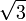
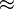
1.7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909 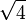

2 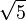
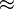
2.2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638 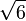
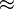
2.4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457 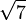
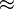
2.6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230 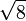
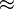
2.8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924 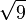

3 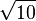
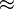
3.1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639 
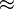
3.3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609 
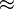
3.4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818 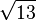
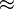
3.6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293 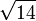
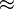
3.7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307 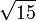
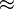
3.8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937 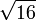

4 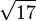
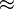
4.1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338 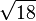
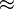
4.2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386 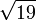
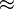
4.3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203 
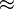
4.4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418 51276
As periodic continued fractions
One of the most intriguing results from the study of irrational numbers as continued fractions was obtained by Joseph Louis Lagrange circa 1780. Lagrange found that the square root of any non-square positive integer can be represented by a periodic continued fraction. That is, in which a certain pattern of digits occurs over and over in the denominators (see example below the table). In a sense these square roots are the very simplest irrational numbers, because they can be represented with a simple repeating pattern of digits.
-
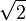

[1; 2, 2, ...] 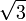

[1; 1, 2, 1, 2, ...] 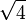

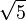

[2; 4, 4, ...] 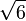

[2; 2, 4, 2, 4, ...] 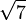

[2; 1, 1, 1, 4, 1, 1, 1, 4, ...] 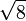

[2; 1, 4, 1, 4, ...] 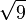

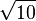

[3; 6, 6, ...] 

[3; 3, 6, 3, 6, ...] 

[3; 2, 6, 2, 6, ...] 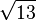

[3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6, ...] 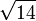

[3; 1, 2, 1, 6, 1, 2, 1, 6, ...] 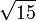

[3; 1, 6, 1, 6, ...] 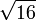

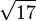

[4; 8, 8, ...] 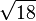

[4; 4, 8, 4, 8, ...] 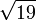

[4; 2, 1, 3, 1, 2, 8, 2, 1, 3, 1, 2, 8, ...] 

[4; 2, 8, 2, 8, ...]
The square bracket notation used above is a sort of mathematical shorthand to conserve space. Written in more traditional notation the simple continued fraction for the square root of 11 – [3; 3, 6, 3, 6, ...] – looks like this:
where the two-digit pattern {3, 6} repeats over and over and over again in the partial denominators.
Geometric construction of the square root
A square root can be constructed with a compass and straightedge. In his Elements, Euclid (fl. 300 BC) gave the construction of the geometric mean of two quantities in two different places: Proposition II.14 and Proposition VI.13. Since the geometric mean of a and b is √ab, one can construct √a simply by taking b = 1.
The construction is also given by Descartes in his La Géométrie, see figure 2 on page 2. However, Descartes made no claim to originality and his audience would have been quite familiar with Euclid.
Another method of geometric construction uses right triangles and induction: √1 can, of course, be constructed, and once √x has been constructed, the right triangle with 1 and √x for its legs has a hypotenuse of √x + 1.
History
The Rhind Mathematical Papyrus is a copy from 1650 BC of an even earlier work and shows us how the Egyptians extracted square roots.
In Ancient India, the knowledge of theoretical and applied aspects of square and square root was at least as old as the Sulba Sutras, dated around 800-500 B.C. (possibly much earlier). A method for finding very good approximations to the square roots of 2 and 3 are given in the Baudhayana Sulba Sutra. Aryabhata in the Aryabhatiya (section 2.4), has given a method for finding the square root of numbers having many digits.
D.E. Smith in History of Mathematics, says, about the existing situation in Europe: "In Europe these methods (for finding out the square and square root) did not appear before Cataneo (1546). He gave the method of Aryabhata for determining the square root".