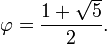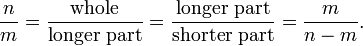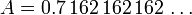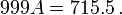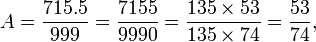Irrational number
Did you know...
SOS Children, an education charity, organised this selection. See http://www.soschildren.org/sponsor-a-child to find out about child sponsorship.
In mathematics, an irrational number is any real number that is not a rational number — that is, it is a number which cannot be expressed as a fraction m/n, where m and n are integers, with n non-zero. Informally, this means numbers that cannot be represented as simple fractions. It can be deduced that they also cannot be represented as terminating or repeating decimals, but the idea is more profound than that. While it may seem strange at first hearing, almost all real numbers are irrational, in a sense which is defined more precisely below. Perhaps the most well known irrational numbers are π and √2 .
When the ratio of lengths of two line segments is irrational, the line segments are also described as being incommensurable, meaning they share no measure in common. A measure of a line segment I in this sense is a line segment J that "measures" I in the sense that some whole number of copies of J laid end-to-end occupy the same length as I.
History
The first proof of the existence of irrational numbers is usually attributed to Hippasus of Metapontum, a Pythagorean who probably discovered them while identifying sides of the pentagram. However Pythagoras believed in the absoluteness of numbers, and could not accept the existence of irrational numbers. He could not disprove their existence through logic, but his beliefs would not accept the existence of irrational numbers and so, as legend had it, he had Hippasus drowned. Theodorus of Cyrene proved the irrationality of the surds of whole numbers up to 17, but stopped there probably because the algebra he used couldn't be applied to the square root of 17. It wasn't until Eudoxus developed a theory of irrational ratios that a strong mathematical foundation of irrational numbers was created. Euclid's Elements Book 10 is dedicated to classification of irrational magnitudes.
The sixteenth century saw the acceptance of negative, integral and fractional numbers. The seventeenth century saw decimal fractions with the modern notation quite generally used by mathematicians. The next hundred years saw imaginary numbers become a powerful tool in the hands of Abraham de Moivre, and especially of Leonhard Euler. The completion of the theory of complex numbers in the nineteenth century entailed the differentiation of irrationals into algebraic and transcendental numbers, the proof of the existence of transcendental numbers, and the resurgence of the scientific study of the theory of irrationals, largely ignored since Euclid. The year 1872 saw the publication of the theories of Karl Weierstrass (by his pupil Kossak), Heine ( Crelle, 74), Georg Cantor (Annalen, 5), and Richard Dedekind. Méray had taken in 1869 the same point of departure as Heine, but the theory is generally referred to the year 1872. Weierstrass's method has been completely set forth by Salvatore Pincherle in 1880, and Dedekind's has received additional prominence through the author's later work (1888) and the recent endorsement by Paul Tannery (1894). Weierstrass, Cantor, and Heine base their theories on infinite series, while Dedekind founds his on the idea of a cut (Schnitt) in the system of real numbers, separating all rational numbers into two groups having certain characteristic properties. The subject has received later contributions at the hands of Weierstrass, Kronecker (Crelle, 101), and Méray.
Continued fractions, closely related to irrational numbers (and due to Cataldi, 1613), received attention at the hands of Euler, and at the opening of the nineteenth century were brought into prominence through the writings of Lagrange. Dirichlet also added to the general theory, as have numerous contributors to the applications of the subject.
Lambert proved (1761) that π cannot be rational, and that en is irrational if n is rational (unless n = 0). While Lambert's proof is often said to be incomplete, modern assessments support it as satisfactory, and in fact for its time unusually rigorous. Legendre (1794), after introducing the Bessel-Clifford function, provided a proof to show that π2 is irrational, whence it follows immediately that π is irrational also. The existence of transcendental numbers was first established by Liouville (1844, 1851). Later, Georg Cantor (1873) proved their existence by a different method, that showed that every interval in the reals contains transcendental numbers. Charles Hermite (1873) first proved  transcendental, and Ferdinand von Lindemann (1882), starting from Hermite's conclusions, showed the same for π. Lindemann's proof was much simplified by Weierstrass (1885), still further by David Hilbert (1893), and was finally made elementary by Adolf Hurwitz and Paul Albert Gordan.
transcendental, and Ferdinand von Lindemann (1882), starting from Hermite's conclusions, showed the same for π. Lindemann's proof was much simplified by Weierstrass (1885), still further by David Hilbert (1893), and was finally made elementary by Adolf Hurwitz and Paul Albert Gordan.
Example proofs
The square root of 2
The irrationality of the square root of 2 may be proved by assuming it is rational and inferring a contradiction, called an argument by reductio ad absurdum. The following argument appeals twice to the fact that the square of an odd integer is always odd.
If √2 is rational it has the form m/n for integers m, n not both even. Then m² = 2n² whence m is even, say m = 2p. Thus 4p² = 2n² so 2p² = n² whence n is also even, a contradiction .
Another proof
The following reductio ad absurdum argument is less well-known. It uses the additional information √2 > 1.
- Assume that √2 is a rational number. This would mean that there exist integers m and n with n ≠ 0 such that m/n = √2.
- Then √2 can also be written as an irreducible fraction m/n with positive integers, because √2 > 0.
- Then
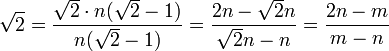 , because
, because  .
. - Since √2 > 1, it follows that m > n, which in turn implies that m > 2n – m.
- So the fraction m/n for √2, which according to (2) is already in lowest terms, is represented by (3) in strictly lower terms. This is a contradiction, so the assumption that √2 is rational must be false.
Similarly, assume an isosceles right triangle whose leg and hypotenuse have respective integer lengths n and m. By the Pythagorean theorem, the ratio m/n equals √2. It is possible to construct by a classic compass and straightedge construction a smaller isosceles right triangle whose leg and hypotenuse have respective lengths m − n and 2n − m. That construction proves the irrationality of √2 by the kind of method that was employed by ancient Greek geometers.
The square root of 10 and beyond
If √10 is rational, say m/n, then m2 = 10n2. However, in decimal notation, every square ends in an even number of zeros. So then m2 and 10n2 in decimal must end in respectively an even and odd number of zeros, a contradiction.
More generally, in any radix r that is not itself a square, every square ends in an even numbers of zeros, whence √10r in radix r is irrational, that is, √r is irrational. It follows that the only integers with rational square roots are squares. As a case in point, 2 is not a square, and 2 in binary is 102. (Note the convention of subscripting nondecimal numerals with their radix, to avoid ambiguity. As part of that convention the subscripts are understood to be in decimal, not being subscripted themselves.)
To go even further, we can consider mk = r × nk for any integers r and k. If r ≠ uk for any integer u, then r has at least one prime factor p raised to an exponent that is not divisible by k. As all the exponents in the prime factorization of mk are divisible by k, for the equation to hold, the prime factorization of nk must contain p raised to a power that is also not divisible by k. But this is clearly impossible. Thus, for any integers r and k, k√r is irrational if r ≠ uk for any integer u. This result also follows from the fact that raising a non-integral rational number to an integral power can never equal an integer besides 1.
The golden ratio
When a line segment is divided into two disjoint subsegments in such a way that the ratio of the whole to the longer part equals the ratio of the longer part to the shorter part, then that ratio is the golden ratio, equal to
Assume this is a rational number n/m in lowest terms. Take n to be the length of the whole and m the length of the longer part. Then n > m, and the length of the shorter part is n − m. Then we have
However, this puts a fraction already in lowest terms into lower terms—a contradiction. Therefore the initial assumption, that the golden ratio is rational, is false.
Logarithms
Perhaps the numbers most easily proved to be irrational are certain logarithms. Here is a proof by reductio ad absurdum that log23 is irrational:
- Assume log23 is rational. For some positive integers m and n, we have log23 = m/n.
- It follows that 2m/n = 3.
- Raise each side to the n power, find 2m = 3n.
- But 2 to any integer power greater than 0 is even (because at least one of its prime factors is 2) and 3 to any integer power greater than 0 is odd (because none of its prime factors is 2), so the original assumption is false.
Cases such as log102 can be treated similarly.
Transcendental and algebraic irrationals
Almost all irrational numbers are transcendental and all transcendental numbers are irrational: the article on transcendental numbers lists several examples. er and πr are irrational if r ≠ 0 is rational; eπ is also irrational.
Another way to construct irrational numbers is as irrational algebraic numbers, i.e. as zeros of polynomials with integer coefficients: start with a polynomial equation
- p(x) = an xn + an-1 xn−1 + ... + a1 x + a0 = 0
where the coefficients ai are integers. Suppose you know that there exists some real number x with p(x) = 0 (for instance if n is odd and an is non-zero, then because of the intermediate value theorem). The only possible rational roots of this polynomial equation are of the form r/s where r is a divisor of a0 and s is a divisor of an; there are only finitely many such candidates which you can all check by hand. If neither of them is a root of p, then x must be irrational. For example, this technique can be used to show that x = (21/2 + 1)1/3 is irrational: we have (x3 − 1)2 = 2 and hence x6 − 2x3 − 1 = 0, and this latter polynomial does not have any rational roots (the only candidates to check are ±1).
Because the algebraic numbers form a field, many irrational numbers can be constructed by combining transcendental and algebraic numbers. For example 3π+2, π + √2 and e√3 are irrational (and even transcendental).
Decimal expansions
The decimal expansion of an irrational number never repeats or terminates, unlike a rational number.
To show this, suppose we divide integers n by m (where m is nonzero). When long division is applied to the division of n by m, only m remainders are possible. If 0 appears as a remainder, the decimal expansion terminates. If 0 never occurs, then the algorithm can run at most m − 1 steps without using any remainder more than once. After that, a remainder must recur, and then the decimal expansion repeats!
Conversely, suppose we are faced with a recurring decimal, we can prove that it is a fraction of two integers. For example:
Here the length of the repitend is 3. We multiply by 103:
Note that since we multiplied by 10 to the power of the length of the repeating part, we shifted the digits to the left of the decimal point by exactly that many positions. Therefore, the tail end of 1000A matches the tail end of A exactly. Here, both 1000A and A have repeating 162 at the end.
Therefore, when we subtract A from both sides, the tail end of 1000A cancels out of the tail end of A:
Then
which is a quotient of integers and therefore a rational number.
Open questions
It is not known whether π + e or π − e is irrational or not. In fact, there is no pair of non-zero integers m and n for which it is known whether mπ + ne is irrational or not. Moreover, it is not known whether the set {π, e} is algebraically independent over Q.
It is not known whether 2e, πe, π√2, Catalan's constant, or the Euler-Mascheroni gamma constant γ are irrational.
The set of all irrationals
Since the reals form an uncountable set of which the rationals are a countable subset, the complementary set of irrationals is uncountable.
Under the usual ( Euclidean) distance function d(x, y) = |x − y|, the real numbers are a metric space and hence also a topological space. Restricting the Euclidean distance function gives the irrationals the structure of a metric space. Since the subspace of irrationals is not closed, the induced metric is not complete. However, being a G-delta set -- i.e., a countable intersection of open subsets -- in a complete metric space, the space of irrationals is topologically complete: that is, there is a metric on the irrationals inducing the same topology as the restriction of the Euclidean metric, but with respect to which the irrationals are complete. One can see this without knowing the aforementioned fact about G-delta sets: the continued fraction expansion of an irrational number defines a homeomorphism from the space of irrationals to the space of all sequences of positive integers, which is easily seen to be completely metrizable.
Furthermore, the set of all irrationals is a disconnected metric space.

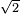 is irrational.
is irrational.