
Mean
Background Information
This content from Wikipedia has been selected by SOS Children for suitability in schools around the world. Click here to find out about child sponsorship.
In statistics, mean has two related meanings:
- the arithmetic mean (and is distinguished from the geometric mean or harmonic mean).
- the expected value of a random variable, which is also called the population mean.
It is sometimes stated that the 'mean' means average. This is incorrect if "mean" is taken in the specific sense of "arithmetic mean" as there are different types of averages: the mean, median, and mode. For instance, average house prices almost always use the median value for the average.
For a real-valued random variable X, the mean is the expectation of X. Note that not every probability distribution has a defined mean (or variance); see the Cauchy distribution for an example.
For a data set, the mean is the sum of the observations divided by the number of observations. The mean is often quoted along with the standard deviation: the mean describes the central location of the data, and the standard deviation describes the spread.
An alternative measure of dispersion is the mean deviation, equivalent to the average absolute deviation from the mean. It is less sensitive to outliers, but less mathematically tractable.
As well as statistics, means are often used in geometry and analysis; a wide range of means have been developed for these purposes, which are not much used in statistics. These are listed below.
Examples of means
Arithmetic mean
The arithmetic mean is the "standard" average, often simply called the "mean".
The mean may often be confused with the median or mode. The mean is the arithmetic average of a set of values, or distribution; however, for skewed distributions, the mean is not necessarily the same as the middle value (median), or the most likely (mode). For example, mean income is skewed upwards by a small number of people with very large incomes, so that the majority have an income lower than the mean. By contrast, the median income is the level at which half the population is below and half is above. The mode income is the most likely income, and favors the larger number of people with lower incomes. The median or mode are often more intuitive measures of such data.
That said, many skewed distributions are best described by their mean - such as the Exponential and Poisson distributions.
For example, the arithmetic mean of 34, 27, 45, 55, 22, 34 (six values) is (34+27+45+55+22+34)/6 = 217/6 ≈ 36.167.
Geometric mean
The geometric mean is an average that is useful for sets of numbers that are interpreted according to their product and not their sum (as is the case with the arithmetic mean). For example rates of growth.
For example, the geometric mean of 34, 27, 45, 55, 22, 34 (six values) is (34×27×45×55×22×34)1/6 = 1,699,493,4001/6 = 34.545.
Harmonic mean
The harmonic mean is an average which is useful for sets of numbers which are defined in relation to some unit, for example speed (distance per unit of time).
For example, the harmonic mean of the numbers 34, 27, 45, 55, 22, and 34 is
Generalized means
Power mean
The generalized mean, also known as the power mean or Hölder mean, is an abstraction of the quadratic, arithmetic, geometric and harmonic means. It is defined by
By choosing the appropriate value for the parameter m we get
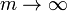 |
maximum |
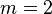 |
quadratic mean, |
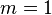 |
arithmetic mean, |
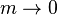 |
geometric mean, |
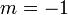 |
harmonic mean, |
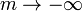 |
minimum. |
f-mean
This can be generalized further as the generalized f-mean
and again a suitable choice of an invertible 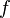 will give
will give
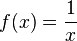 |
harmonic mean, |
 |
power mean, |
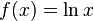 |
geometric mean. |
Weighted arithmetic mean
The weighted arithmetic mean is used, if one wants to combine average values from samples of the same population with different sample sizes:
The weights 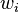 represent the bounds of the partial sample. In other applications they represent a measure for the reliability of the influence upon the mean by respective values.
represent the bounds of the partial sample. In other applications they represent a measure for the reliability of the influence upon the mean by respective values.
Truncated mean
Sometimes a set of numbers (the data) might be contaminated by inaccurate outliers, i.e. values which are much too low or much too high. In this case one can use a truncated mean. It involves discarding given parts of the data at the top or the bottom end, typically an equal amount at each end, and then taking the arithmetic mean of the remaining data. The number of values removed is indicated as a percentage of total number of values.
Interquartile mean
The interquartile mean is a specific example of a truncated mean. It is simply the arithmetic mean after removing the lowest and the highest quarter of values.
assuming the values have been ordered.
Mean of a function
In calculus, and especially multivariable calculus, the mean of a function is loosely defined as the average value of the function over its domain. In one variable, the mean of a function f(x) over the interval (a,b) is defined by
(See also mean value theorem.) In several variables, the mean over a relatively compact domain U in a Euclidean space is defined by
This generalizes the arithmetic mean. On the other hand, it is also possible to generalize the geometric mean to functions by defining the geometric mean of f to be
More generally, in measure theory and probability theory either sort of mean plays an important role. In this context, Jensen's inequality places sharp estimates on the relationship between these two different notions of the mean of a function.
Mean of angles
Most of the usual means fail on circular quantities, like angles, daytimes, fractional parts of real numbers. For those quantities you need a mean of circular quantities.
Other means
- Arithmetic-geometric mean
- Arithmetic-harmonic mean
- Cesàro mean
- Chisini mean
- Contraharmonic mean
- Elementary symmetric mean
- Geometric-harmonic mean
- Heinz mean
- Heronian mean
- Identric mean
- Least squares mean
- Lehmer mean
- Logarithmic mean
- Median
- Root mean square
- Stolarsky mean
- Temporal mean
- Weighted geometric mean
- Weighted harmonic mean
- Rényi's entropy (a generalized f-mean)
Properties
The most general method for defining a mean or average, y, takes any function of a list g(x_1, x_2, ..., x_n), which is symmetric under permutation of the members of the list, and equates it to the same function with the value of the mean replacing each member of the list: g(x_1, x_2, ..., x_n) = g(y, y, ..., y). All means share some properties and additional properties are shared by the most common means. Some of these properties are collected here.
Weighted mean
A weighted mean 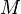 is a function which maps tuples of positive numbers to a positive number (
is a function which maps tuples of positive numbers to a positive number (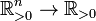 ).
).
- " Fixed point":
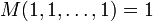
- Homogenity:
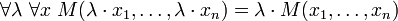
-
- (using vector notation:
 )
)
- (using vector notation:
- Monotony:
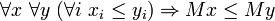
It follows
- Boundedness:
![\forall x\ M x \in [\min x, \max x]](../../images/135/13510.png)
- Continuity:
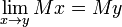
- Sketch of a proof: Because
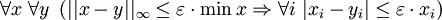 and
and 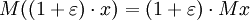 it follows
it follows 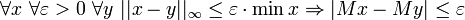 .
.
- There are means, which are not differentiable. For instance, the maximum number of a tuple is considered a mean (as an extreme case of the power mean, or as a special case of a median), but is not differentiable.
- All means listed above, with the exception of most of the Generalized f-means, satisfy the presented properties.
- If
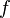 is bijective, then the generalized f-mean satisfies the fixed point property.
is bijective, then the generalized f-mean satisfies the fixed point property. - If
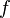 is strictly monotonic, then the generalized f-mean satisfy also the monotony property.
is strictly monotonic, then the generalized f-mean satisfy also the monotony property. - In general a generalized f-mean will miss homogenity.
- If
The above properties imply techniques to construct more complex means:
If  are weighted means,
are weighted means, 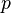 is a positive real number, then
is a positive real number, then 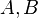 with
with
are also a weighted mean.
Unweighted mean
Intuitively spoken, an unweighted mean is a weighted mean with equal weights. Since our definition of weighted mean above does not expose particular weights, equal weights must be asserted by a different way. A different view on homogeneous weighting is, that the inputs can be swapped without altering the result.
Thus we define 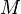 being an unweighted mean if it is a weighted mean and for each permutation
being an unweighted mean if it is a weighted mean and for each permutation 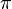 of inputs, the result is the same. Let
of inputs, the result is the same. Let 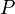 be the set of permutations of
be the set of permutations of 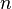 -tuples.
-tuples.
- Symmetry:

Analogously to the weighted means, if 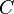 is a weighted mean and
is a weighted mean and 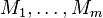 are unweighted means,
are unweighted means, 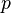 is a positive real number, then
is a positive real number, then 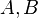 with
with
are also unweighted means.
Convert unweighted mean to weighted mean
An unweighted mean can be turned into a weighted mean by repeating elements. This connection can also be used to state that a mean is the weighted version of an unweighted mean. Say you have the unweighted mean 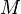 and weight the numbers by natural numbers
and weight the numbers by natural numbers  . (If the numbers are rational, then multiply them with the least common denominator.) Then the corresponding weighted mean
. (If the numbers are rational, then multiply them with the least common denominator.) Then the corresponding weighted mean 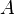 is obtained by
is obtained by
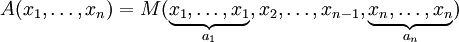 .
.
Means of tuples of different sizes
If a mean 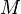 is defined for tuples of several sizes, then one also expects that the mean of a tuple is bounded by the means of partitions. More precisely
is defined for tuples of several sizes, then one also expects that the mean of a tuple is bounded by the means of partitions. More precisely
- Given an arbitrary tuple
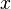 , which is partitioned into
, which is partitioned into 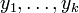 , then it holds
, then it holds 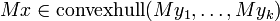 . (See Convex hull)
. (See Convex hull)
Mathematics education
In many state and government curriculum standards, students are traditionally expected to learn either the meaning or formula for computing the mean by the fourth grade. However, in many standards-based mathematics curricula, students are encouraged to invent their own methods, and may not be taught the traditional method. Reform based texts such as TERC in fact discourage teaching the traditional "add the numbers and divide by the number of items" method in favour of spending more time on the concept of median, which does not require division. However, mean can be computed with a simple four-function calculator, while median requires a computer. The same teacher guide devotes several pages on how to find the median of a set, which is judged to be simpler than finding the mean.
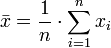
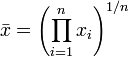
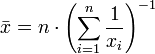
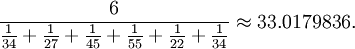
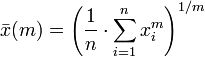
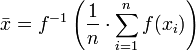
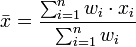
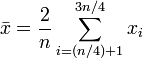
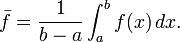
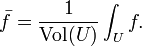
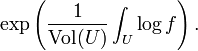
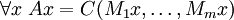
![\forall x\ B x = \sqrt[p]{C(x_1^p, \dots, x_n^p)}](../../images/135/13518.png)
![\forall x\ B x = \sqrt[p]{M_1(x_1^p, \dots, x_n^p)}](../../images/135/13521.png)
