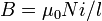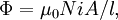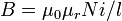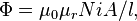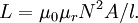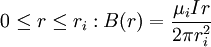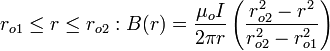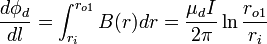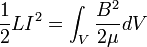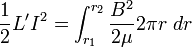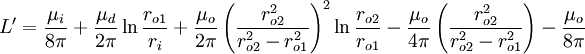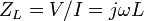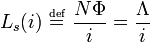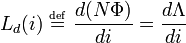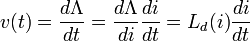Inductance
About this schools Wikipedia selection
The articles in this Schools selection have been arranged by curriculum topic thanks to SOS Children volunteers. Click here to find out about child sponsorship.
| Electromagnetism |
|---|
 |
|
Electrostatics
|
|
Magnetostatics
|
|
Electrodynamics
|
|
Electrical network
|
|
Covariant formulation
Electromagnetic tensor
( stress–energy tensor)
|
In electromagnetism and electronics, inductance is the property of a conductor by which a change in current in the conductor "induces" (creates) a voltage ( electromotive force) in both the conductor itself (self-inductance) and in any nearby conductors (mutual inductance). This effect derives from two fundamental observations of physics: First, that a steady current creates a steady magnetic field ( Oersted's law) and second, that a time-varying magnetic field induces a voltage in a nearby conductor ( Faraday's law of induction). From Lenz's law, in an electric circuit, a changing electric current through a circuit that has inductance induces a proportional voltage which opposes the change in current (self inductance). The varying field in this circuit may also induce an e.m.f. in a neighbouring circuit (mutual inductance).
The term 'inductance' was coined by Oliver Heaviside in February 1886. It is customary to use the symbol L for inductance, in honour of the physicist Heinrich Lenz. In the SI system the unit of inductance is the henry, named in honour of the scientist who discovered inductance, Joseph Henry.
To add inductance to a circuit, electrical or electronic components called inductors are used, typically consisting of coils of wire to concentrate the magnetic field and so that the magnetic field is linked into the circuit more than once.
The relationship between the self inductance L of an electrical circuit in henries, voltage, and current is
where v denotes the voltage in volts and i the current in amperes. The voltage across an inductor is equal to the product of its inductance and the time rate of change of the current through it.
All practical circuits have some inductance, which may provide either beneficial or detrimental effects. In a tuned circuit inductance is used to provide a frequency selective circuit. Practical inductors may be used to provide filtering or energy storage in a system. The inductance of a transmission line is one of the properties that determines its characteristic impedance; balancing the inductance and capacitance of cables is important for distortion-free telegraphy and telephony. The inductance of long power transmission lines limits the AC power that can be sent over them. Sensitive circuits such as microphone and computer network cables may use special cable constructions to limit the mutual inductance between signal circuits.
In circuit analysis
The generalization to the case of K electrical circuits with currents im and voltages vm reads
Inductance here is a symmetric matrix. The diagonal coefficients Lm,m are called coefficients of self inductance, the off-diagonal elements are called coefficients of mutual inductance. The coefficients of inductance are constant as long as no magnetizable material with nonlinear characteristics is involved. This is a direct consequence of the linearity of Maxwell's equations in the fields and the current density. The coefficients of inductance become functions of the currents in the nonlinear case, see nonlinear inductance.
Derivation from Faraday's law of inductance
The inductance equations above are a consequence of Maxwell's equations. There is a straightforward derivation in the important case of electrical circuits consisting of thin wires.
Consider a system of K wire loops, each with one or several wire turns. The flux linkage of loop m is given by
Here Nm denotes the number of turns in loop m, Φm the magnetic flux through this loop, and Lm,n are some constants. This equation follows from Ampere's law - magnetic fields and fluxes are linear functions of the currents. By Faraday's law of induction we have
where vm denotes the voltage induced in circuit m. This agrees with the definition of inductance above if the coefficients Lm,n are identified with the coefficients of inductance. Because the total currents Nnin contribute to Φm it also follows that Lm,n is proportional to the product of turns NmNn.
Inductance and magnetic field energy
Multiplying the equation for vm above with imdt and summing over m gives the energy transferred to the system in the time interval dt,
This must agree with the change of the magnetic field energy W caused by the currents. The integrability condition
requires Lm,n=Ln,m. The inductance matrix Lm,n thus is symmetric. The integral of the energy transfer is the magnetic field energy as a function of the currents,
This equation also is a direct consequence of the linearity of Maxwell's equations. It is helpful to associate changing electric currents with a build-up or decrease of magnet field energy. The corresponding energy transfer requires or generates a voltage. A mechanical analogy in the K=1 case with magnetic field energy (1/2)Li2 is a body with mass M, velocity u and kinetic energy (1/2)Mu2. The rate of change of velocity (current) multiplied with mass (inductance) requires or generates a force (an electrical voltage).
Coupled inductors
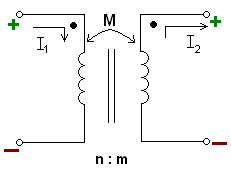
Mutual inductance occurs when the change in current in one inductor induces a voltage in another nearby inductor. It is important as the mechanism by which transformers work, but it can also cause unwanted coupling between conductors in a circuit.
The mutual inductance, M, is also a measure of the coupling between two inductors. The mutual inductance by circuit i on circuit j is given by the double integral Neumann formula, see calculation techniques
The mutual inductance also has the relationship:
where
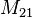 is the mutual inductance, and the subscript specifies the relationship of the voltage induced in coil 2 due to the current in coil 1.
is the mutual inductance, and the subscript specifies the relationship of the voltage induced in coil 2 due to the current in coil 1.- N1 is the number of turns in coil 1,
- N2 is the number of turns in coil 2,
- P21 is the permeance of the space occupied by the flux.
The mutual inductance also has a relationship with the coupling coefficient. The coupling coefficient is always between 1 and 0, and is a convenient way to specify the relationship between a certain orientation of inductors with arbitrary inductance:
where
- k is the coupling coefficient and 0 ≤ k ≤ 1,
- L1 is the inductance of the first coil, and
- L2 is the inductance of the second coil.
Once the mutual inductance, M, is determined from this factor, it can be used to predict the behaviour of a circuit:
where
- V1 is the voltage across the inductor of interest,
- L1 is the inductance of the inductor of interest,
- dI1/dt is the derivative, with respect to time, of the current through the inductor of interest,
- dI2/dt is the derivative, with respect to time, of the current through the inductor that is coupled to the first inductor, and
- M is the mutual inductance.
The minus sign arises because of the sense the current I2 has been defined in the diagram. With both currents defined going into the dots the sign of M will be positive.
When one inductor is closely coupled to another inductor through mutual inductance, such as in a transformer, the voltages, currents, and number of turns can be related in the following way:
where
- Vs is the voltage across the secondary inductor,
- Vp is the voltage across the primary inductor (the one connected to a power source),
- Ns is the number of turns in the secondary inductor, and
- Np is the number of turns in the primary inductor.
Conversely the current:
where
- Is is the current through the secondary inductor,
- Ip is the current through the primary inductor (the one connected to a power source),
- Ns is the number of turns in the secondary inductor, and
- Np is the number of turns in the primary inductor.
Note that the power through one inductor is the same as the power through the other. Also note that these equations don't work if both transformers are forced (with power sources).
When either side of the transformer is a tuned circuit, the amount of mutual inductance between the two windings determines the shape of the frequency response curve. Although no boundaries are defined, this is often referred to as loose-, critical-, and over-coupling. When two tuned circuits are loosely coupled through mutual inductance, the bandwidth will be narrow. As the amount of mutual inductance increases, the bandwidth continues to grow. When the mutual inductance is increased beyond a critical point, the peak in the response curve begins to drop, and the centre frequency will be attenuated more strongly than its direct sidebands. This is known as overcoupling.
Calculation techniques
In the most general case, inductance can be calculated from Maxwell's equations. Many important cases can be solved using simplifications. Where high frequency currents are considered, with skin effect, the surface current densities and magnetic field may be obtained by solving the Laplace equation. Where the conductors are thin wires, self inductance still depends on the wire radius and the distribution of the current in the wire. This current distribution is approximately constant (on the surface or in the volume of the wire) for a wire radius much smaller than other length scales.
Mutual inductance of two wire loops
The mutual inductance by a filamentary circuit i on a filamentary circuit j is given by the double integral Neumann formula
The symbol μ0 denotes the magnetic constant (4π×10−7 H/m), Ci and Cj are the curves spanned by the wires, Rij is the distance between two points. See a derivation of this equation.
Self-inductance of a wire loop
Formally the self-inductance of a wire loop would be given by the above equation with i = j. The problem, however, is that 1/R now becomes infinite, making it necessary to take the finite wire radius a and the distribution of the current in the wire into account. There remain the contribution from the integral over all points with |R| > a/2 and a correction term,
Here a and l denote radius and length of the wire, and Y is a constant that depends on the distribution of the current in the wire: Y = 0 when the current flows in the surface of the wire ( skin effect), Y = 1/4 when the current is homogeneous across the wire. This approximation is accurate when the wires are long compared to their cross-sectional dimensions.
Method of images
In some cases different current distributions generate the same magnetic field in some section of space. This fact may be used to relate self inductances ( method of images). As an example consider the two systems:
- A wire at distance d/2 in front of a perfectly conducting wall (which is the return)
- Two parallel wires at distance d, with opposite current
The magnetic field of the two systems coincides (in a half space). The magnetic field energy and the inductance of the second system thus are twice as large as that of the first system.
Relation between inductance and capacitance
Inductance per length L' and capacitance per length C' are related to each other in the special case of transmission lines consisting of two parallel perfect conductors of arbitrary but constant cross section,
Here ε and µ denote dielectric constant and magnetic permeability of the medium the conductors are embedded in. There is no electric and no magnetic field inside the conductors (complete skin effect, high frequency). Current flows down on one line and returns on the other. Signals will propagate along the transmission line at the speed of electromagnetic radiation in the non-conductive medium enveloping the conductors.
Self-inductance of simple electrical circuits in air
The self-inductance of many types of electrical circuits can be given in closed form. Examples are listed in the table.
| Type | Inductance | Comment |
|---|---|---|
| Single layer solenoid |
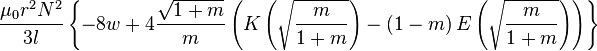
|
 : Number of turns : Number of turnsr: Radius l: Length w = r/l 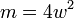 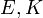 : Elliptic integrals : Elliptic integrals |
| Coaxial cable, high frequency |
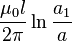 |
a1: Outer radius a: Inner radius l: Length |
| Circular loop | 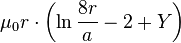 |
r: Loop radius a: Wire radius |
| Rectangle | 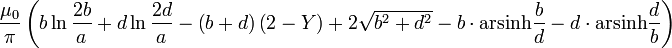 |
b, d: Border length d >> a, b >> a a: Wire radius |
| Pair of parallel wires |
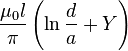 |
a: Wire radius d: Distance, d ≥ 2a l: Length of pair |
| Pair of parallel wires, high frequency |
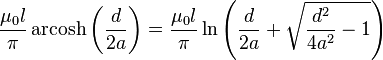 |
a: Wire radius d: Distance, d ≥ 2a l: Length of pair |
| Wire parallel to perfectly conducting wall |
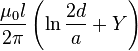 |
a: Wire radius d: Distance, d ≥ a l: Length |
| Wire parallel to conducting wall, high frequency |
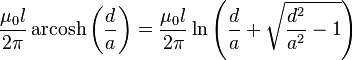 |
a: Wire radius d: Distance, d ≥ a l: Length |
The symbol μ0 denotes the magnetic constant (4π×10−7 H/m). For high frequencies the electric current flows in the conductor surface ( skin effect), and depending on the geometry it sometimes is necessary to distinguish low and high frequency inductances. This is the purpose of the constant Y: Y = 0 when the current is uniformly distributed over the surface of the wire (skin effect), Y = 1/4 when the current is uniformly distributed over the cross section of the wire. In the high frequency case, if conductors approach each other, an additional screening current flows in their surface, and expressions containing Y become invalid.
Inductance with physical symmetry
Inductance of a solenoid
A solenoid is a long, thin coil, i.e. a coil whose length is much greater than the diameter. Under these conditions, and without any magnetic material used, the magnetic flux density  within the coil is practically constant and is given by
within the coil is practically constant and is given by
where  is the magnetic constant,
is the magnetic constant,  the number of turns,
the number of turns, 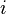 the current and
the current and 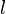 the length of the coil. Ignoring end effects the total magnetic flux through the coil is obtained by multiplying the flux density
the length of the coil. Ignoring end effects the total magnetic flux through the coil is obtained by multiplying the flux density 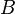 by the cross-section area
by the cross-section area 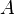 and the number of turns
and the number of turns  :
:
When this is combined with the definition of inductance,
it follows that the inductance of a solenoid is given by:
A table of inductance for short solenoids of various diameter to length ratios has been calculated by Dellinger, Whittmore, and Ould
This, and the inductance of more complicated shapes, can be derived from Maxwell's equations. For rigid air-core coils, inductance is a function of coil geometry and number of turns, and is independent of current.
Similar analysis applies to a solenoid with a magnetic core, but only if the length of the coil is much greater than the product of the relative permeability of the magnetic core and the diameter. That limits the simple analysis to low-permeability cores, or extremely long thin solenoids. Although rarely useful, the equations are,
where 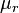 the relative permeability of the material within the solenoid,
the relative permeability of the material within the solenoid,
from which it follows that the inductance of a solenoid is given by:
where N is squared because of the definition of inductance.
Note that since the permeability of ferromagnetic materials changes with applied magnetic flux, the inductance of a coil with a ferromagnetic core will generally vary with current.
Inductance of a coaxial line
Let the inner conductor have radius 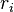 and permeability
and permeability 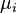 , let the dielectric between the inner and outer conductor have permeability
, let the dielectric between the inner and outer conductor have permeability 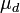 , and let the outer conductor have inner radius
, and let the outer conductor have inner radius 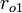 , outer radius
, outer radius 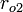 , and permeability
, and permeability 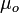 . Assume that a DC current
. Assume that a DC current 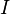 flows in opposite directions in the two conductors, with uniform current density. The magnetic field generated by these currents points in the azimuthal direction and is a function of radius
flows in opposite directions in the two conductors, with uniform current density. The magnetic field generated by these currents points in the azimuthal direction and is a function of radius  ; it can be computed using Ampère's law:
; it can be computed using Ampère's law:
The flux per length 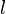 in the region between the conductors can be computed by drawing a surface containing the axis:
in the region between the conductors can be computed by drawing a surface containing the axis:
Inside the conductors, L can be computed by equating the energy stored in an inductor, 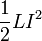 , with the energy stored in the magnetic field:
, with the energy stored in the magnetic field:
For a cylindrical geometry with no 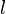 dependence, the energy per unit length is
dependence, the energy per unit length is
where 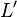 is the inductance per unit length. For the inner conductor, the integral on the right-hand-side is
is the inductance per unit length. For the inner conductor, the integral on the right-hand-side is  ; for the outer conductor it is
; for the outer conductor it is 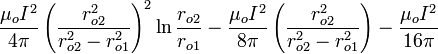
Solving for 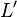 and summing the terms for each region together gives a total inductance per unit length of:
and summing the terms for each region together gives a total inductance per unit length of:
However, for a typical coaxial line application we are interested in passing (non-DC) signals at frequencies for which the resistive skin effect cannot be neglected. In most cases, the inner and outer conductor terms are negligible, in which case one may approximate
Phasor circuit analysis and impedance
Using phasors, the equivalent impedance of an inductance is given by:
where
- j is the imaginary unit,
- L is the inductance,
- ω = 2πf is the angular frequency,
- f is the frequency and
- ωL = XL is the inductive reactance.
Nonlinear inductance
Many inductors make use of magnetic materials. These materials over a large enough range exhibit a nonlinear permeability with such effects as saturation. This in-turn makes the resulting inductance a function of the applied current. Faraday's Law still holds but inductance is ambiguous and is different whether you are calculating circuit parameters or magnetic fluxes.
The secant or large-signal inductance is used in flux calculations. It is defined as:
The differential or small-signal inductance, on the other hand, is used in calculating voltage. It is defined as:
The circuit voltage for a nonlinear inductor is obtained via the differential inductance as shown by Faraday's Law and the chain rule of calculus.
There are similar definitions for nonlinear mutual inductances.
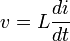

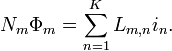
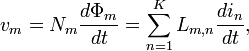


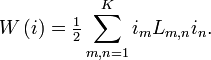

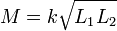
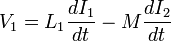
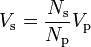
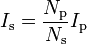
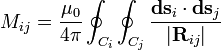


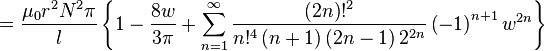
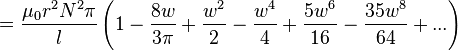 for w << 1
for w << 1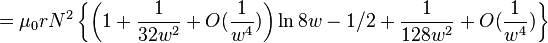 for w >> 1
for w >> 1