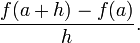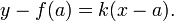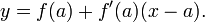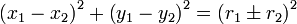Tangent
Background to the schools Wikipedia
This selection is made for schools by a children's charity read more. Sponsor a child to make a real difference.
In geometry, the tangent line (or simply the tangent) to a curve at a given point is the straight line that "just touches" the curve at that point (in the sense explained more precisely below). As it passes through the point of tangency, the tangent line is "going in the same direction" as the curve, and in this sense it is the best straight-line approximation to the curve at that point. The same definition applies to space curves and curves in n-dimensional Euclidean space.
In a similar way, the tangent plane to a surface at a given point is the plane that "just touches" the surface at that point. The concept of a tangent is one of the most fundamental notions in differential geometry and has been extensively generalized — see Tangent space.
The word "tangent" comes from the Latin tangere, meaning "to touch".
Tangent line to a curve
The intuitive notion that a tangent "just touches" a curve can be made more explicit by considering the sequence of straight lines ( secant lines) passing through two points, A and B, that lie on the curve. The tangent at A is the limit of the progression of secant lines as B moves ever closer to A. The existence and uniqueness of the tangent line depends on a certain type of mathematical smoothness, known as "differentiability". For example, if two circular arcs meet at a sharp point (a vertex) then there is no uniquely defined tangent at the vertex because the limit of the progression of secant lines depends on the direction in which "point B" approaches the vertex.
In most cases commonly encountered, the tangent to a curve does not cross the curve at the point of tangency (though it may, when continued, cross the curve at other places away from the point of tangency). This is true, for example, of all tangents to a circle or a parabola. However, at exceptional points called inflection points, the tangent line does cross the curve at the point of tangency. An example is the point (0,0) on the graph of the cubic parabola y = x3.
Conversely, it may happen that the curve lies entirely on one side of a straight line passing through a point on it, and yet this straight line is not a tangent line. This is the case, for example, for a line passing through the vertex of a triangle and not interecting the triangle — where the tangent line does not exist for the reasons explained above. In convex geometry, such lines are called supporting lines.
Analytical approach
The geometric idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. In the second book of his Geometry René Descartes said of the problem of constructing the tangent to a curve, "And I dare say that this is not only the most useful and most general problem in geometry that I know, but even that I have ever desired to know."
Intuitive description
Suppose that a curve is given as the graph of a function, y = f(x). To find the tangent line at the point p = (a, f(a)), consider another nearby point q = (a + h, f(a + h)) on the curve. The slope of the secant line passing through p and q is equal to the difference quotient
As the point q approaches p, which corresponds to making h smaller and smaller, the difference quotient should approach a certain limiting value k, which is the slope of the tangent line at the point p. If k is known, the equation of the tangent line can be found in the point-slope form:
More rigorous description
To make the preceding reasoning rigorous, one has to explain what is meant by the difference quotient approaching a certain limiting value k. The precise mathematical formulation was given by Cauchy in the 19th century and is based on the notion of limit. Suppose that the graph does not have a break or a sharp edge at p and it is neither plumb nor too wiggly near p. Then there is a unique value of k such that as h approaches 0, the difference quotient gets closer and closer to k, and the distance between them becomes negligible compared with the size of h, if h is small enough. This leads to the definition of the slope of the tangent line to the graph as the limit of the difference quotients for the function f. This limit is the derivative of the function f at x = a, denoted f ′(a). Using derivatives, the equation of the tangent line can be stated as follows:
Calculus provides rules for computing the derivatives of functions that are given by formulas, such as the power function, trigonometric functions, exponential function, logarithm, and their various combinations. Thus equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus.
When the method fails
Calculus also demonstrates that there are functions and points on their graphs for which the limit determining the slope of the tangent line does not exist. For these points the function f is non-differentiable. There are two possible reasons for the method of finding the tangents based on the limits and derivatives to fail: either the geometric tangent exists, but it is a vertical line, which cannot be given in the point-slope form since it does not have a slope, or the graph is too badly behaved to admit a geometric tangent.
The graph y = x1/3 illustrates the first possibility: here the difference quotient at a = 0 is equal to h1/3/h = h− 2/3, which becomes very large as h approaches 0. The tangent line to this curve at the origin is vertical.
The graph y = |x| of the absolute value function consists of two straight lines with different slopes joined at the origin. As a point q approaches the origin from the right, the secant line always has slope 1. As a point q approaches the origin from the left, the secant line always has slope −1. Therefore, there is no unique tangent to the graph at the origin (although in a certain sense, there are two half-tangents, corresponding to two possible directions of approaching the origin).
Tangent circles
Two circles, with radii of ri and centers at (xi , yi), for i=1, 2 are said to be tangent to each other if
Surfaces and higher-dimensional manifolds
The tangent plane to a surface at a given point p is defined in an analogous way to the tangent line in the case of curves. It is the best approximation of the surface by a plane at p, and can be obtained as the limiting position of the planes passing through 3 distinct points on the surface close to p as these points converge to p. More generally, there is a k-dimensional tangent space at each point of a k-dimensional manifold in the n-dimensional Euclidean space.