Conic Sections

A conic section (or just conic) is a curve obtained as the intersection of a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2. There are a number of other geometric definitions possible. The four types of conic section are the hyperbola, the parabola, the ellipse, and the circle, though the circle can be considered to be a special case of the ellipse. 

The type of a conic corresponds to its eccentricity. Conics with eccentricity less than $1$ are ellipses, conics with eccentricity equal to $1$ are parabolas, and conics with eccentricity greater than $1$ are hyperbolas. In the focus-directrix definition of a conic, the circle is a limiting case of the ellipse with an eccentricity of $0$. In modern geometry, certain degenerate cases, such as the union of two lines, are included as conics as well.

System of Equations

In a system of equations, two or more relationships are stated among variables. A system is solvable as long as there are as many simultaneous equations as variables. If each equation is graphed, the solution for the system can be found at the point where all the functions meet. The solution can be found either by inspection of a graph, typically by using graphing or plotting software, or algebraically.

Nonlinear Systems

Nonlinear systems of equations, such as conic sections, include at least one equation that is nonlinear. A nonlinear equation is defined as an equation possessing at least one term that is raised to a power of 2 or more. When graphed, these equations produce curved lines.

Since at least one function has curvature, it is possible for nonlinear systems of equations to contain multiple solutions. As with linear systems of equations, substitution can be used to solve nonlinear systems for one variable and then the other.

Solving nonlinear systems of equations algebraically is similar to doing the same for linear systems of equations. However, subtraction of one equation from another can become impractical if the two equations have different terms, which is more commonly the case in nonlinear systems.

Example

Consider, for example, the following system of equations:

$\begin{aligned} y &= x^2 \; \qquad (1) \\ y &= x + 6 \quad (2) \end{aligned}$

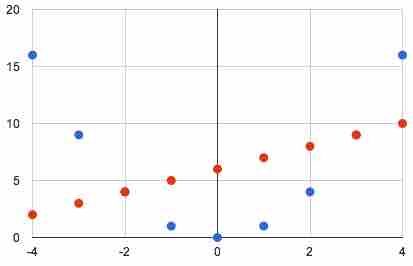
Integer values of $y=x^2$ (blue) and $y=x+6$ (red)

The parabola (blue) falls below the line (red) between $x=-2$ and $x=3$. For all values of $x$ less than $-2$ and greater than $3$, points on the parabola are above the line.

We can solve this system algebraically by using equation $(1)$ as a substitution. The quantity $x^2$ must be equivalent to the quantity $y$, so we substitute $x^2$ for $y$ in equation $(2)$:

$\displaystyle{ \begin{aligned} y&=x+6 \\ x^2&=x+6 \end{aligned} }$

This quadratic equation can be solved by moving all the equation's components to the left before using the quadratic formula:

$x^2-x-6=0$

Using the quadratic formula, with $a = 1$, $b = -2$, and $c = -6$, it can be determined that the solutions are $x = -2$ and $x = 3$.

The solutions for $x$ can then be plugged into either of the original systems to find the value of $y$. In this example, we will use equation $(1)$:

$\displaystyle{ \begin{aligned} y&=x^2 \\ y&=(-2)^2 \\ y&=4 \end{aligned} }$

$\displaystyle{ \begin{aligned} y&=x^2 \\ y&=(3)^2\\ y&=9 \end{aligned} }$

Thus, for $x = -2$, $y = 4$, and for $x = 3$, $y = 9$.

Our final solutions are: $(-2,4)$ and $(3,9)$.