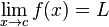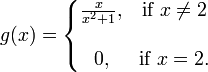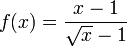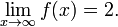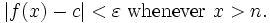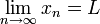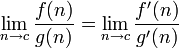Limit (mathematics)

Related subjects: Mathematics

Did you know...

Arranging a Wikipedia selection for schools in the developing world without internet was an initiative by SOS Children. Sponsor a child to make a real difference.

The Wikibook Calculus has a page on the topic of: Limits

In mathematics, the concept of a "limit" is used to describe the behaviour of a function as its argument either "gets close" to some point, or as it becomes arbitrarily large; or the behaviour of a sequence's elements as their index increases indefinitely. Limits are used in calculus and other branches of mathematical analysis to define derivatives and continuity.

The concept of the "limit of a function" is further generalized to the concept of topological net, while the limit of a sequence is closely related to limit and direct limit in category theory.

Limit of a function

Suppose ƒ(x) is a real-valued function and c is a real number. The expression:

$\lim_{x \to c}f(x) = L$

means that ƒ(x) can be made to be as close to L as desired by making x sufficiently close to c. In that case, we say that "the limit of ƒ of x, as x approaches c, is L". Note that this statement can be true even if 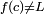$\scriptstyle f(c) \neq L$ . Indeed, the function ƒ(x) need not even be defined at c. Two examples help illustrate this.

Consider $f(x)=\frac{x}{x^2+1}$ as x approaches 2. In this case, f(x) is defined at 2 and equals its limit of 0.4:

f(1.9)	f(1.99)	f(1.999)	f(2)	f(2.001)	f(2.01)	f(2.1)
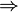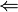0.4121	0.4012	0.4001	$\Rightarrow$ 0.4 $\Leftarrow$	0.3998	0.3988	0.3882

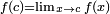As x approaches 2, ƒ(x) approaches 0.4 and hence we have $\scriptstyle \lim_{x\to 2}f(x)=0.4$ . In the case where $\scriptstyle f(c) = \lim_{x\to c} f(x)$ , ƒ is said to be continuous at x = c. But it is not always the case. Consider

$g(x)=\left\{\begin{matrix} \frac{x}{x^2+1}, & \mbox{if }x\ne 2 \\ \\ 0, & \mbox{if }x=2. \end{matrix}\right.$

The limit of g(x) as x approaches 2 is 0.4 (just as in ƒ(x)), but 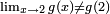$\scriptstyle \lim_{x\to 2}g(x)\neq g(2)$ ; g is not continuous at x = 2.

Or, consider the case where ƒ(x) is undefined at x = c.

$f(x) = \frac{x - 1}{\sqrt{x} - 1}$

In this case, as x approaches 1, f(x) is undefined at x = 1 but the limit equals 2:

f(0.9)	f(0.99)	f(0.999)	f(1.0)	f(1.001)	f(1.01)	f(1.1)
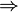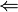1.95	1.99	1.999	$\Rightarrow$ undef $\Leftarrow$	2.001	2.010	2.10

Thus, f(x) can be made arbitrarily close to the limit of 2 just by making x sufficiently close enough to 1.

Formal definition

Karl Weierstrass formally defined a limit as follows:

Let f be a function defined on an open interval containing c (except possibly at c) and let L be a real number.

$\lim_{x \to c}f(x) = L$

means that

for each real ε > 0 there exists a real δ > 0 such that for all x with 0 < |x − c| < δ, we have |f(x) − L| < ε.

The formal definition of a limit is sometimes called the delta-epsilon form because it uses the Greek letters delta (δ) and epsilon (ε). The use of the particular Greek letters δ and ε is merely traditional; the definition would, of course, be unchanged if different letters or symbols were used.

Caution: It should be noted that this definition provides a way to recognize a limit without providing a way to calculate it. One often needs to find a limit using informal methods, especially when f(x) is discontinuous at c, for example, when f is a ratio with a denominator that becomes 0 at c. One should check that the result actually meets the Weierstrass definition in such cases.

Limit of a function at infinity

A related concept to limits as x approaches some finite number is the limit as x approaches positive or negative infinity. This does not literally mean that the difference between x and infinity becomes small, since infinity is not a real number; rather, it means that x either grows without bound positively (positive infinity) or grows without bound negatively (negative infinity).

For example, consider f(x) = 2x/(x + 1).

f(100) = 1.9802
f(1000) = 1.9980
f(10000) = 1.9998

As x becomes extremely large, the value of f(x) approaches 2, and the value of f(x) can be made as close to 2 as one could wish just by picking x sufficiently large. In this case, we say that the limit of f(x) as x approaches infinity is 2. In mathematical notation,

$\lim_{x \to \infty} f(x) = 2.$

Formally, we have the definition

$\lim_{x \to \infty} f(x) = c$ if and only if for each ε > 0 there exists an n such that

$|f(x) - c| < \varepsilon \text{ whenever } x > n.$

Note that the n in the definition will generally depend on ε. A similar definition applies for 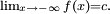$\scriptstyle \lim_{x \to -\infty} f(x)=c.$

If one considers the domain of f to be the extended real number line, then the limit of a function at infinity can be considered as a special case of limit of a function at a point.

Limit of a sequence

Consider the following sequence: 1.79, 1.799, 1.7999,... We could observe that the numbers are "approaching" 1.8, the limit of the sequence.

Formally, suppose x₁, x₂, ... is a sequence of real numbers. We say that the real number L is the limit of this sequence and we write

$\lim_{n \to \infty} x_n = L$

if and only if for every real number ε > 0 there exists a natural number n₀ (which will depend on ε) such that for all n > n₀ we have |x_n − L| < ε.

Intuitively, this means that eventually all elements of the sequence get as close as we want to the limit, since the absolute value |x_n − L| is the distance between x_n and L. Not every sequence has a limit; if it does, we call it convergent, otherwise divergent. One can show that a convergent sequence has only one limit.

The limit of a sequence and the limit of a function are closely related. On one hand, the limit of a sequence is simply the limit at infinity of a function defined on natural numbers. On the other hand, a limit of a function f at x, if it exists, is the same as the limit of the sequence x_n = f(x + 1/n).

Useful Identities

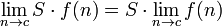$\lim_{n \to c} S \sdot f(n) = S \sdot \lim_{n \to c} f(n)$ , where S is a scalar multiplier.
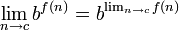$\lim_{n \to c} b^{f(n)} = b^{\lim_{n \to c} f(n)}$ , where b is a constant.

The following rules are only valid if the limits on the righthand side exists and are finite.

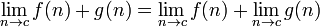
$\lim_{n \to c} f(n) + g(n) = \lim_{n \to c} f(n) + \lim_{n \to c} g(n)$
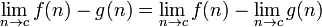
$\lim_{n \to c} f(n) - g(n) = \lim_{n \to c} f(n) - \lim_{n \to c} g(n)$
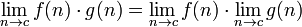
$\lim_{n \to c} f(n) \sdot g(n) = \lim_{n \to c} f(n) \sdot \lim_{n \to c} g(n)$
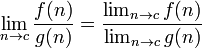$\lim_{n \to c} \frac{f(n)}{g(n)} = \frac{\lim_{n \to c} f(n)}{\lim_{n \to c} g(n)}$ , if the denominator containing the limit does not equal zero

If any of the limits in the righthand side is undefined or infinite, the rules does not necessarily work.

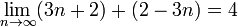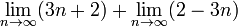For example, $\lim_{n \to \infty} (3n+2) + (2-3n) = 4$ but $\lim_{n \to \infty} (3n+2) + \lim_{n \to \infty}(2-3n)$ is undefined.

Limits of extra interest

$\lim_{n \to 0} \frac{\sin n}{n} = 1$
$\lim_{n \to 0} \frac{1 - \cos n}{n} = 0$
$\lim_{n \to \infty} \frac{\sin n}{n} = 0$
$\lim_{n \to \infty} \frac{\cos n}{n} = 0$

l'Hôpital's rule

This rule uses derivatives and has a conditional usage. It can only be used on indeterminate forms.

$\lim_{n \to c} \frac{f(n)}{g(n)} = \lim_{n \to c} \frac{f'(n)}{g'(n)}$

For example: 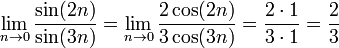$\lim_{n \to 0} \frac{\sin (2n)}{\sin (3n)} = \lim_{n \to 0} \frac{2 \cos (2n)}{3 \cos (3n)} = \frac{2 \sdot 1}{3 \sdot 1} = \frac{2}{3}$

Summations

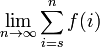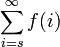
A short way to write the limit $\lim_{n \to \infty} \sum_{i=s}^{n} f(i)$ is $\sum_{i=s}^{\infty} f(i)$

Topological net

All of the above notions of limit can be unified and generalized to arbitrary topological spaces by introducing topological nets and defining their limits. The article on nets elaborates on this.

An alternative is the concept of limit for filters on topological spaces.

Limit in category theory

Retrieved from " http://en.wikipedia.org/w/index.php?title=Limit_(mathematics)&oldid=189022086"