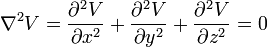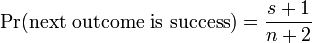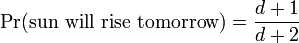Pierre-Simon Laplace
Did you know...
This content from Wikipedia has been selected by SOS Children for suitability in schools around the world. Click here for more information on SOS Children.
| Pierre-Simon, marquis de Laplace | |
|---|---|
 Posthumous portrait by Madame Feytaud, 1842 |
|
| Born | 1749-03-23 Beaumont-en-Auge, Normandy, France |
| Died | March 5, 1827 (aged 77) Paris, France |
| Residence | France |
| Citizenship | French |
| Fields | Astronomy Mathematics |
| Institutions | École Militaire (1769-1776) |
| Known for | Work in Celestial Mechanics Laplace's equation Laplace Operator/Laplacian Laplace transform |
Pierre-Simon, marquis de Laplace ( March 23 1749 - March 5 1827) was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste ( Celestial Mechanics) (1799-1825). This seminal work translated the geometric study of classical mechanics, used by Isaac Newton, to one based on calculus, opening up a broader range of problems.
He formulated Laplace's equation, and invented the Laplace transform which appears in many branches of mathematical physics, a field that he took a leading role in forming. The Laplacian differential operator, widely used in applied mathematics, is also named after him.
Independently from Immanuel Kant, he formulated the nebular hypothesis of the origin of the solar system and was one of the first scientists to postulate the existence of black holes and the notion of gravitational collapse.
He is remembered as one of the greatest scientists of all time, sometimes referred to as a French Newton or Newton of France, with a natural phenomenal mathematical faculty possessed by none of his contemporaries.
He became a count of the First French Empire in 1806 and was named a marquis in 1817, after the Bourbon Restoration.
Early life
Pierre Simon Laplace was born in Beaumont-en-Auge, Normandy.
According to Rouse Ball ('A Short Account of the History of Mathematics', 4th edition, 1908), he was the son of a small cottager or perhaps a farm-labourer, and owed his education to the interest excited in some wealthy neighbours by his abilities and engaging presence. Very little is known of his early years, for when he became distinguished he had the pettiness to hold himself aloof both from his relatives and from those who had assisted him. It would seem from a pupil he became an usher in the school at Beaumont; but, having procured a letter of introduction to D'Alembert, he went to Paris to push his fortune. However, Pearson (1929, Biometrika) is scathing about the inaccuracies in Rouse Ball's account and states that ".. Caen was probably in Laplace's day the most intellectually active of all the towns of Normandy. It was here that Laplace was educated and was provisionally a professor. It was here he wrote his first paper published in the Melanges of the Royal Society of Turin, Tome iv. 1766-1769, at least two years before he went at 22 or 23 to Paris in 1771. Thus before he was 20 he was in touch with Joseph Louis Lagrange in Turin. He did not go to Paris a raw self-taught country lad with only a peasant background I In 176S at the age of sixteen Laplace left the "School of the Duke of Orleans" in Beaumont and went to the University of Caen, where he appears to have studied for five years. The "Ecole militaire" of Beaumont did not replace the old school until 1770.
His father was Pierre Laplace, a cider merchant and his mother was Marie-Anne Sochon. His parents were from comfortable bourgeois families. Laplace attended a school in the village run at a Benedictine priory, his father intending that he would be ordained in the Roman Catholic Church, and at sixteen he was sent to further his father's intention at the University of Caen, reading theology.
At the university, he was mentored by two enthusiastic teachers of mathematics, Christophe Gadbled and Pierre Le Canu, who awoke his zeal for the subject. Laplace never graduated in theology but left for Paris with a letter of introduction from Le Canu to Jean le Rond d'Alembert. There is an apocryphal story that, aged nineteen, he solved overnight the problem that D'Alembert set him for submission the following week, then solved a harder problem the following night. D'Alembert was impressed and recommended him for a teaching place in the École Militaire.
With a secure income and undemanding teaching, Laplace now threw himself into original research and, in the next seventeen years, 1771-1787, he produced much of his original work in astronomy.
Laplace further impressed the Marquis de Condorcet, and even in 1771 Laplace felt that he was entitled to membership in the French Academy of Sciences. However, in that year, admission went to Alexandre-Théophile Vandermonde and in 1772 to Antoine-Joseph Cousin. Laplace was disgruntled and early in 1773 canvassed a move to Berlin. However, Condorcet became permanent secretary of the Académie in February and Laplace was elected associate member on 31 March.
He was married in 1788 and his son was born in 1789.
Analysis, probability and astronomical stability
Laplace's early published work in 1771 started with differential equations and finite differences but he was already starting to think about the mathematical and philosophical concepts of probability and statistics. However, before his election to the Académie in 1773, he had already drafted two papers that would establish his reputation. The first, Mémoire sur la probabilité des causes par les événements was ultimately published in 1774 while the second paper, published in 1776, further elaborated his statistical thinking and also began his systematic work on celestial mechanics and the stability of the solar system. The two disciplines would always be interlinked in his mind. "Laplace took probability as an instrument for repairing defects in knowledge." Laplace's work on probability and statistics is discussed below with his mature work on the Analytic theory of probabilities.
Stability of the solar system
Sir Isaac Newton had published his Philosophiae Naturalis Principia Mathematica in 1687 in which he gave a derivation of Kepler's laws, which describe the motion of the planets, from his laws of motion and his law of universal gravitation. However, though Newton had privately developed the methods of calculus, all his published work used cumbersome geometric reasoning, unsuitable to account for the more subtle higher-order effects of interactions between the planets. Newton himself had doubted the possibility of a mathematical solution to the whole, even concluding that periodic divine intervention was necessary to guarantee the stability of the solar system. Dispensing with the hypothesis of divine intervention would be the major activity of Laplace's scientific life. As of 2007, it is generally regarded that Laplace's methods on their own, though critical to the development of the theory, are not sufficiently precise to demonstrate the stability of the solar system.
One particular problem from observational astronomy was the apparent instability whereby Jupiter's orbit appeared to be shrinking while that of Saturn was expanding. The problem had been tackled by Leonhard Euler in 1748 and Joseph Louis Lagrange in 1763 but without success. In 1776, Laplace published a memoir in which he first explored the possible influences of a purported luminiferous ether or of a law of gravitation that did not act instantaneously. He ultimately returned to an intellectual investment in Newtonian gravity. Euler and Lagrange had made a practical approximation by ignoring small terms in the equations of motion. Laplace noted that though the terms themselves were small, when integrated over time they could become important. Laplace carried his analysis into the higher-order terms, up to and including the cubic. Using this more exact analysis, Laplace concluded that any two planets and the sun must be in mutual equilibrium and thereby launched his work on the stability of the solar system. Gerald James Whitrow described the achievement as "the most important advance in physical astronomy since Newton".
Laplace had a wide knowledge of all sciences and dominated all discussions in the Académie. Laplace seems to have regarded analysis merely as a means of attacking physical problems, though the ability with which he invented the necessary analysis is almost phenomenal. As long as his results were true he took but little trouble to explain the steps by which he arrived at them; he never studied elegance or symmetry in his processes, and it was sufficient for him if he could by any means solve the particular question he was discussing.
On the figure of the Earth
During the years 1784-1787 he produced some memoirs of exceptional power. Prominent among these is one read in 1783, reprinted as Part II of Théorie du Mouvement et de la figure elliptique des planètes in 1784, and in the third volume of the Méchanique céleste. In this work, Laplace completely determined the attraction of a spheroid on a particle outside it. This is memorable for the introduction into analysis of spherical harmonics or Laplace's coefficients, and also for the development of the use of the potential, a name first used by George Green in 1828.
Spherical harmonics
In 1783, in a paper sent to the Académie, Adrien-Marie Legendre had introduced what are now known as associated Legendre functions. If two points in a plane have polar co-ordinates (r, θ) and (r ', θ'), where r ' ≥ r, then, by elementary manipulation, the reciprocal of the distance between the points, d, can be written as:
![\frac{1}{d} = \frac{1}{r'} \left [ 1 - 2 \cos (\theta' - \theta) \frac{r}{r'} + \left ( \frac{r}{r'} \right ) ^2 \right ] ^{- \tfrac{1}{2}}](../../images/101/10106.png)
This expression can be expanded in powers of r/r ' using Newton's generalized binomial theorem to give:
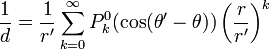
The sequence of functions P0k(cosф) is the set of so-called "associated Legendre functions" and their usefulness arises from the fact that every function of the points on a circle can be expanded as a series of them.
Laplace, with scant regard for credit to Legendre, made the non-trivial extension of the result to three dimensions to yield a more general set of functions, the spherical harmonics or Laplace coefficients. As of 2007, the latter term is not in common use. Every function of the points on a sphere can be expanded as a series of them.
Potential theory
This paper is also remarkable for the development of the idea of the scalar potential. The gravitational force acting on a body is, in modern language, a vector, having magnitude and direction. A potential function is a scalar function that defines how the vectors will behave. A scalar function is computationally and conceptually easier to deal with than a vector function.
Alexis Clairault had first suggested the idea in 1743 while working on a similar problem though he was using Newtonian-type geometric reasoning. Laplace described Clairault's work as being "in the class of the most beautiful mathematical productions". However, Rouse Ball alleges that the idea "was appropriated from Joseph Louis Lagrange, who had used it in his memoirs of 1773, 1777 and 1780".
Laplace applied the language of calculus to the potential function and shows that it always satisfies the differential equation:
- and on this result his subsequent work on gravitational attraction was based. The quantity 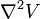 has been termed the concentration of
has been termed the concentration of 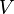 and its value at any point indicates the "excess" of the value of
and its value at any point indicates the "excess" of the value of 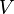 there over its mean value in the neighbourhood of the point. Laplace's equation, a special case of Poisson's equation, appears ubiquitously in mathematical physics. Wherever a vector force acts on a body, the concept of a potential can be applied and Laplace's equation occurs in fluid dynamics, electromagnetism and other areas. According to some writers this follows at once from the fact that
there over its mean value in the neighbourhood of the point. Laplace's equation, a special case of Poisson's equation, appears ubiquitously in mathematical physics. Wherever a vector force acts on a body, the concept of a potential can be applied and Laplace's equation occurs in fluid dynamics, electromagnetism and other areas. According to some writers this follows at once from the fact that 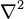 is a scalar operator. Rouse Ball speculated that it might be seen as "the outward sign" of one the "prior forms" in Kant's theory of perception.
is a scalar operator. Rouse Ball speculated that it might be seen as "the outward sign" of one the "prior forms" in Kant's theory of perception.
The spherical harmonics turn out to be critical to practical solutions of Laplace's equation. Laplace's equation in spherical coordinates, such as are used for mapping the sky, can be simplified, using the method of separation of variables into a radial part, depending solely on distance from the Earth (say), and an angular or spherical part. The solution to the spherical part of the equation can be expressed as a series of Laplace's spherical harmonics, simplifying practical computation.
Planetary inequalities
This memoir was followed by another on planetary inequalities, which was presented in three sections in 1784, 1785, and 1786. This deals mainly with the explanation of the "great inequality" of Jupiter and Saturn. Laplace showed by general considerations that the mutual action of two planets could never largely affect the eccentricities and inclinations of their orbits; and that the peculiarities of the Jovian system were due to the near approach to commensurability of the mean motions of Jupiter and Saturn: further developments of these theorems on planetary motion were given in his two memoirs of 1788 and 1789. It was on these data that Delambre computed his astronomical tables.
It had been observed since ancient times that the Moon's position in the sky was drifting over time. In 1693, Edmond Halley had shown that the rate of the drift was increasing, an effect known as the secular acceleration of the Moon. Laplace gave an explanation in 1787 in terms of changes in the eccentricity of the Earth's orbit. However, in 1853, John Couch Adams went on to show that Laplace had only considered the radial force on the moon and not the tangential, and hence had failed to explain more than half of the drift. The other half was subsequently shown to be due to tidal acceleration. However, Laplace was still able to use his result to complete the proof of the stability of the whole solar system on the assumption that it consists of a collection of rigid bodies moving in a vacuum.
All the memoirs above alluded to were presented to the Académie des sciences, and they are printed in the Mémoires présentés par divers savants.
Celestial mechanics
Laplace now set himself the task to write a work which should "offer a complete solution of the great mechanical problem presented by the solar system, and bring theory to coincide so closely with observation that empirical equations should no longer find a place in astronomical tables." The result is embodied in the Exposition du système du monde and the Mécanique céleste.
The former was published in 1796, and gives a general explanation of the phenomena, but omits all details. It contains a summary of the history of astronomy. This summary procured for its author the honour of admission to the forty of the French Academy and is commonly esteemed one of the masterpieces of French literature, though it is not altogether reliable for the later periods of which it treats.
Laplace developed the nebular hypothesis of the formation of the solar system, first suggested by Emanuel Swedenborg and expanded by Immanuel Kant, a hypothesis that continues to dominate accounts of the origin of planetary systems. According to Laplace's description of the hypothesis, the solar system had evolved from a globular mass of incandescent gas rotating around an axis through its centre of mass. As it cooled this mass contracted and successive rings broke off from its outer edge. These rings in their turn cooled, and finally condensed into the planets, while the sun represented the central core which was still left. On this view Laplace predicted that the more distant planets would be older than those nearer the sun.
The idea of the nebular hypothesis had been outlined by Immanuel Kant in 1755, and he had also suggested "meteoric aggregations" and tidal friction as causes affecting the formation of the solar system. It is probable that Laplace was not aware of this.
Laplace's analytical discussion of the solar system is given in his Méchanique céleste published in five volumes. The first two volumes, published in 1799, contain methods for calculating the motions of the planets, determining their figures, and resolving tidal problems. The third and fourth volumes, published in 1802 and 1805, contain applications of these methods, and several astronomical tables. The fifth volume, published in 1825, is mainly historical, but it gives as appendices the results of Laplace's latest researches. Laplace's own investigations embodied in it are so numerous and valuable that it is regrettable to have to add that many results are appropriated from writers with scanty or no acknowledgement, and the conclusions - which have been described as the organized result of a century of patient toil - are frequently mentioned as if they were due to Laplace.
Jean-Baptiste Biot, who assisted Laplace in revising it for the press, says that Laplace himself was frequently unable to recover the details in the chain of reasoning, and, if satisfied that the conclusions were correct, he was content to insert the constantly recurring formula, "Il est aisé à voir." The Méchanique céleste is not only the translation of the Principia into the language of the differential calculus, but it completes parts of which Newton had been unable to fill in the details. The work was more finely tuned by Félix Tisserand but Laplace's treatise will always remain a standard authority.
Arcueil
In 1806, Laplace bought a house in Arcueil, then a village and not yet absorbed into the Paris conurbation. Claude Louis Berthollet was a near neighbour and the pair formed the nucleus of an informal scientific circle, latterly known as the Society of Arcueil. Because of Laplace and Berthollet's closeness to Napoleon, they effectively controlled advancement in the scientific establishment and admission to the more prestigious offices. The Society built up a complex pyramid of patronage.
Science as prediction
Laplace went in state to beg Napoleon to accept a copy of his work, who had heard that the book contained no mention of God. Napoleon, who was fond of putting embarrassing questions, received it with the remark, "M. Laplace, they tell me you have written this large book on the system of the universe, and have never even mentioned its Creator." Laplace, who, though the most supple of politicians, was as stiff as a martyr on every point of his philosophy, drew himself up and answered bluntly, "Je n'avais pas besoin de cette hypothèse-là." (I did not need to make such an assumption). Napoleon, greatly amused, told this reply to Lagrange, who exclaimed, "Ah! c'est une belle hypothèse; ça explique beaucoup de choses" (Ah! that is a beautiful assumption; it explains many things). Laplace then declared: "Cette hypothèse, Sire, explique en effet tout, mais ne permet de prédire rien. En tant que savant, je me dois de vous fournir des travaux permettant des prédictions" ("This hypothesis, Sire, does explain everything, but does not permit to predict anything. As a scholar, I must provide you with works permitting predictions." - quoted by Ian Stewart and Jack Cohen). Laplace thus defined science as a predicting tool.
Black holes
Laplace also came close to propounding the concept of the black hole. He pointed out that there could be massive stars whose gravity is so great that not even light could escape from their surface (see escape velocity). Laplace also speculated that some of the nebulae revealed by telescopes may not be part of the Milky Way and might actually be galaxies themselves. Thus, he anticipated the major discovery of Edwin Hubble, some 100 years before it happened.
Analytic theory of probabilities
In 1812, Laplace issued his Théorie analytique des probabilités in which he laid down many fundamental results in statistics. In 1819, he published a popular account of his work on probability. This book bears the same relation to the Théorie des probabilités that the Système du monde does to the Méchanique céleste.
Probability-generating function
The method of estimating the ratio of the number of favourable cases, compared to the whole number of possible cases, had been previously indicated by Laplace in a paper written in 1779. It consists of treating the successive values of any function as the coefficients in the expansion of another function, with reference to a different variable. The latter is therefore called the probability-generating function of the former. Laplace then shows how, by means of interpolation, these coefficients may be determined from the generating function. Next he attacks the converse problem, and from the coefficients he finds the generating function; this is effected by the solution of a finite difference equation. The method is cumbersome and leads most of the time to a normal probability distribution the so called Laplace-Gauss distribution, not to be confused with the Laplace distribution.
Least squares
This treatise includes an exposition of the method of least squares, a remarkable testimony to Laplace's command over the processes of analysis. The method of least squares for the combination of numerous observations had been given empirically by Carl Friedrich Gauss and Legendre, but the fourth chapter of this work contains a formal proof of it, on which the whole of the theory of errors has been since based. This was affected only by a most intricate analysis specially invented for the purpose, but the form in which it is presented is so meagre and unsatisfactory that, in spite of the uniform accuracy of the results, it was at one time questioned whether Laplace had actually gone through the difficult work he so briefly and often incorrectly indicates.
Inductive probability
While he conducted much research in physics, another major theme of his life's endeavours was probability theory. In his Essai philosophique sur les probabilités, Laplace set out a mathematical system of inductive reasoning based on probability, which we would today recognise as Bayesian. One well-known formula arising from his system is the rule of succession. Suppose that some trial has only two possible outcomes, labeled "success" and "failure". Under the assumption that little or nothing is known a priori about the relative plausibilities of the outcomes, Laplace derived a formula for the probability that the next trial will be a success.
where s is the number of previously observed successes and n is the total number of observed trials. It is still used as an estimator for the probability of an event if we know the event space, but only have a small number of samples.
The rule of succession has been subject to much criticism, partly due to the example which Laplace chose to illustrate it. He calculated that the probability that the sun will rise tomorrow, given that it has never failed to in the past, was
where d is the number of times the sun has risen in the past times. This result has been derided as absurd, and some authors have concluded that all applications of the Rule of Succession are absurd by extension. However, Laplace was fully aware of the absurdity of the result; immediately following the example, he wrote, "But this number [i.e., the probability that the sun will rise tomorrow] is far greater for him who, seeing in the totality of phenomena the principle regulating the days and seasons, realizes that nothing at the present moment can arrest the course of it."
Laplace's demon
Laplace strongly believed in causal determinism, which is expressed in the following quote from the introduction to the Essai:
| “ | We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes. | ” |
This intellect is often referred to as Laplace's demon (in the same vein as Maxwell's demon). Note that the description of the hypothetical intellect described above by Laplace as a demon does not come from Laplace, but from later biographers: Laplace saw himself as a scientist that hoped that humanity would progress in a better scientific understanding of the world, which, if and when eventually completed, would still need a tremendous calculating power to compute it all in a single instant.
Laplace transforms
As early as 1744, Euler, followed by Lagrange, had started looking for solutions of differential equations in the form:
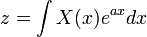 and
and 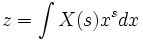 .
.
In 1785, Laplace took the key forward step in using integrals of this form in order to transform a whole difference equation, rather than simply as a form for the solution, and found that the transformed equation was easier to solve than the original.
Other discoveries and accomplishments
Mathematics
Amongst the other discoveries of Laplace in pure and applicable mathematics are:
- Discussion, contemporaneously with Alexandre-Théophile Vandermonde, of the general theory of determinants, (1772);
- Proof that every equation of an even degree must have at least one real quadratic factor;
- Solution of the linear partial differential equation of the second order;
- He was the first to consider the difficult problems involved in equations of mixed differences, and to prove that the solution of an equation in finite differences of the first degree and the second order might be always obtained in the form of a continued fraction; and
- In his theory of probabilities:
- Evaluation of several common definite integrals; and
- General proof of the Lagrange reversion theorem.
Surface tension
Laplace built upon the qualitative work of Thomas Young to develop the theory of capillary action and the Young-Laplace equation.
Speed of sound
Laplace in 1816 was the first to point out that the speed of sound in air depends on the heat capacity ratio. Newton's original theory gave too low a value, because it does not take account of the adiabatic compression of the air that results in a local rise in temperature and pressure. Laplace's investigations in practical physics were confined to those carried on by him jointly with Lavoisier in the years 1782 to 1784 on the specific heat of various bodies.
Political ambitions
As Napoleon's power increased Laplace begged him to give him the post of minister of the interior. Napoleon, who desired the support of men of science, agreed to the proposal, but a little less than six weeks saw the close of Laplace's political career. Napoleon's memorandum on his dismissal is as follows:
Géomètre de premier rang, Laplace ne tarda pas à se montrer administrateur plus que médiocre; dès son premier travail nous reconnûmes que nous nous étions trompé. Laplace ne saisissait aucune question sous son véritable point de vue: il cherchait des subtilités partout, n'avait que des idées problématiques, et portait enfin l'esprit des `infiniment petits' jusque dans l'administration. (Geometrician of the first rank, Laplace was not long in showing himself a worse than average administrator; since his first actions in office we recognized our mistake. Laplace did not consider any question objectively: he sought subtleties everywhere, only conceived problems, and finally carried the spirit of "hair-splitting" into the administration.)
Although Laplace was removed from office it was desirable to retain his allegiance. He was accordingly raised to the senate, and to the third volume of the Mécanique céleste he prefixed a note that of all the truths therein contained the most precious to the author was the declaration he thus made of his devotion towards the peacemaker of Europe. In copies sold after the Bourbon Restoration this was struck out. In 1814 it was evident that the empire was falling; Laplace hastened to tender his services to the Bourbons, and on the restoration was rewarded with the title of marquis. The contempt that his more honest colleagues felt for his conduct in the matter may be read in the pages of Paul Louis Courier. His knowledge was useful on the numerous scientific commissions on which he served, and probably accounts for the manner in which his political insincerity was overlooked; but the pettiness of his character must not make us forget how great were his services to science.
He died in Paris in 1827.
Honours
- Asteroid 4628 Laplace is named for him.
- He is one of only seventy-two people to have their names on the Eiffel Tower.
Quotes
| Wikiquote has a collection of quotations related to: Pierre-Simon Laplace |
- What we know is not much. What we do not know is immense. (attributed)
- I had no need of that hypothesis. ("Je n'avais pas besoin de cette hypothèse-là", as a reply to Napoleon, who had asked why he hadn't mentioned God in his book on astronomy)
- "It is therefore obvious that ..." (frequently used in the Celestial Mechanics when he had proved something and mislaid the proof, or found it clumsy. Notorious as a signal for something true, but hard to prove.)
- The weight of evidence for an extraordinary claim must be proportioned to its strangeness. (known as the Principle of Laplace)