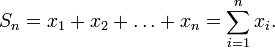Sequence
Background Information
SOS Children volunteers helped choose articles and made other curriculum material SOS Child sponsorship is cool!
For other senses of this word, see
In mathematics, a sequence is an ordered list of objects (or events). Like a set, it contains members (also called elements or terms), and the number of terms (possibly infinite) is called the length of the sequence. Unlike a set, order matters, and the exact same elements can appear multiple times at different positions in the sequence.
For example, (C, R, Y) is a sequence of letters that differs from (Y, C, R), as the ordering matters. Sequences can be finite, as in this example, or infinite, such as the sequence of all even positive integers (2, 4, 6,...).
Examples and notation
There are various and quite different notions of sequences in mathematics, some of which ]ct a A Sequence is a variable-sized Container whose elements are arranged in a strict linear order. It supports insertion and removal of elements. Refinement of Forward Container, Default Constructible Associated types None, except for those of Forward Container. Notation X A type that is a model of Sequence a, b Object of type X T The value type of X t Object of type T p, q Object of type X::iterator n Object of a type convertible to X::size_type
Definitions If a is a Sequence, then p is a valid iterator in a if it is a valid (nonsingular) iterator that is reachable from a.begin(). If a is a Sequence, then [p, q) is a valid range in a if p and q are valid iterators in a and if q is reachable from p.
Valid expressions re not covered by the notations introduced below.
A sequence may be denoted (a1, a2, ...). For shortness, the notation (an) is also used.
A more formal definition of a finite sequence with terms in a set S is a function from {1, 2, ..., n} to S for some n ≥ 0. An infinite sequence in S is a function from {1, 2, ...} (the set of natural numbers without 0) to S.
Sequences may also start from 0, so the first term in the sequence is then a0.
A sequence of a fixed-length n is also called an n-tuple. Finite sequences include the empty sequence ( ) that has no elements.
A function from all integers into a set is sometimes called a bi-infinite sequence, since it may be thought of as a sequence indexed by negative integers grafted onto a sequence indexed by positive integers.
Types and properties of sequences
A subsequence of a given sequence is a sequence formed from the given sequence by deleting some of the elements without disturbing the relative positions of the remaining elements.
If the terms of the sequence are a subset of an ordered set, then a monotonically increasing sequence is one for which each term is greater than or equal to the term before it; if each term is strictly greater than the one preceding it, the sequence is called strictly monotonically increasing. A monotonically decreasing sequence is defined similarly. Any sequence fulfilling the monotonicity property is called monotonic or monotone. This is a special case of the more general notion of monotonic function.
The terms non-decreasing and non-increasing are used in order to avoid any possible confusion with strictly increasing and strictly decreasing, respectively. If the terms of a sequence are integers, then the sequence is an integer sequence. If the terms of a sequence are polynomials, then the sequence is a polynomial sequence.
If S is endowed with a topology, then it becomes possible to consider convergence of an infinite sequence in S. Such considerations involve the concept of the limit of a sequence.
Sequences in analysis
In analysis, when talking about sequences, one will generally consider sequences of the form
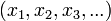 or
or 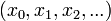
which is to say, infinite sequences of elements indexed by natural numbers.
It may be convenient to have the sequence start with an index different from 1 or 0. For example, the sequence defined by xn = 1/log(n) would be defined only for n ≥ 2. When talking about such infinite sequences, it is usually sufficient (and does not change much for most considerations) to assume that the members of the sequence are defined at least for all indices large enough, that is, greater than some given N.)
The most elementary type of sequences are numerical ones, that is, sequences of real or complex numbers. This type can be generalized to sequences of elements of some vector space. In analysis, the vector spaces considered are often function spaces. Even more generally, one can study sequences with elements in some topological space.
Series
The sum of terms of a sequence is a series. More precisely, if (x1, x2, x3, ...) is a sequence, one may consider the sequence of partial sums (S1, S2, S3, ...), with
Formally, this pair of sequences comprises the series with the terms x1, x2, x3, ..., which is denoted as
If the sequence of partial sums is convergent, one also uses the infinite sum notation for its limit. For more details, see series.
Infinite sequences in theoretical computer science
Infinite sequences of digits (or characters) drawn from a finite alphabet are of particular interest in theoretical computer science. They are often referred to simply as sequences (as opposed to finite strings). Infinite binary sequences, for instance, are infinite sequences of bits (characters drawn from the alphabet {0,1}). The set C = {0, 1}∞ of all infinite, binary sequences is sometimes called the Cantor space.
An infinite binary sequence can represent a formal language (a set of strings) by setting the n th bit of the sequence to 1 if and only if the n th string (in shortlex order) is in the language. Therefore, the study of complexity classes, which are sets of languages, may be regarded as studying sets of infinite sequences.
An infinite sequence drawn from the alphabet {0, 1, ..., b−1} may also represent a real number expressed in the base-b positional number system. This equivalence is often used to bring the techniques of real analysis to bear on complexity classes.
Sequences as vectors
Sequences over a field may also be viewed as vectors in a vector space. Specifically, the set of F-valued sequences (where F is a field) is a function space (in fact, a product space) of F-valued functions over the set of natural numbers.
In particular, the term sequence space usually refers to a linear subspace of the set of all possible infinite sequences with elements in == Doubly-infinite sequences == Normally, the term infinite sequence refers to a sequence which is infinite in one direction, and finite in the other -- the sequence has a first element, but no final element (a singly-infinite sequence). A doubly-infinite sequence is infinite in both directions -- it has neither a first nor a final element. Singly-infinite sequences are functions from the natural numbers (N') to some set, whereas doubly-infinite sequences are functions from the integers (Z) to some set.
One can interpret singly infinite sequences as element of the semigroup ring of the natural numbers ![R[\N]](../../images/146/14691.png) , and doubly infinite sequences as elements of the group ring of the integers
, and doubly infinite sequences as elements of the group ring of the integers ![R[\Z]](../../images/146/14692.png) . This perspective is used in the Cauchy product of sequences.
. This perspective is used in the Cauchy product of sequences.
Ordinal-indexed sequence
An Module:Order_topology ( talk · · hist · links · subpages · tests – results) is a generalization of a sequence. If α is a limit ordinal and X is a set, an α-indexed sequence of elements of X is a function from α to X. In this terminology an ω-indexed sequence is an ordinary sequence.
Sequences and automata
Automata or finite state machines can typically thought of as directed graphs, with edges labeled using some specific alphabet Σ. Most familiar types of automata transition from state to state by reading input letters from Σ, following edges with matching labels; the ordered input for such an automaton forms a sequence called a word (or input word). The sequence of states encountered by the automaton when processing a word is called a run. A nondeterministic automaton may have unlabeled or duplicate out-edges for any state, giving more than one successor for some input letter. This is typically thought of as producing multiple possible runs for a given word, each being a sequence of single states, rather than producing a single run that is a sequence of sets of states; however, 'run' is occasionally used to mean the latter.