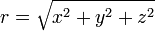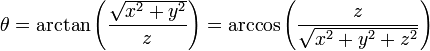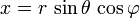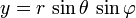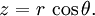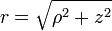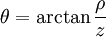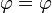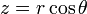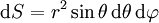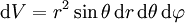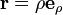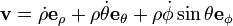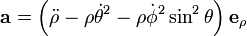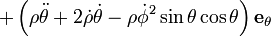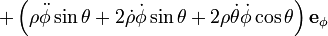Spherical coordinate system
About this schools Wikipedia selection
SOS Children has tried to make Wikipedia content more accessible by this schools selection. To compare sponsorship charities this is the best sponsorship link.
In mathematics, the spherical coordinate system is a coordinate system for representing geometric figures in three dimensions using three coordinates: the radial distance of a point from a fixed origin, the zenith angle from the positive z-axis, and the azimuth angle from the positive x-axis.
Notation
Several different conventions exist for representing the three coordinates. In accordance with the International Organisation for Standardisation ( ISO 31-11), in physics they are typically notated as (r, θ,φ ) for radial distance, zenith, and azimuth, respectively.
In (American) mathematics, the notation for zenith and azimuth are reversed as φ is used to denote the zenith angle and θ is used to denote the azimuthal angle. A further complication is that some mathematics texts list the azimuth before the zenith, but this convention is left-handed and should be avoided. The "math" convention has the advantage of being most compatible in the meaning of θ with the traditional notation for the two-dimensional polar coordinate system and the three-dimensional cylindrical coordinate system, while the "physics" convention has broader acceptance geographically. Some users of the "physics" convention also use φ for polar coordinates to avoid the first problem (as is the standard ISO for cylindrical coordinates). Other notation uses ρ for radial distance. The notation convention of the author of any work pertaining to spherical coordinates should always be checked before using the formulas and equations of that author. This article uses the standard convention.
Definition
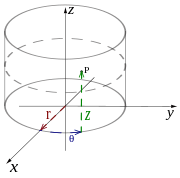
The three coordinates (r, θ, φ) are defined as:
- r ≥ 0 is the distance from the origin to a given point P.
- 0 ≤ θ ≤ π is the angle between the positive z-axis and the line formed between the origin and P.
- 0 ≤ φ < 2π is the angle between the positive x-axis and the line from the origin to the P projected onto the xy-plane.
φ is referred to as the azimuth, while θ is referred to as the zenith, colatitude or polar angle.
θ and φ lose significance when r = 0 and φ loses significance when sin(θ) = 0 (at θ = 0 and θ = π).
To plot a point from its spherical coordinates, go r units from the origin along the positive z-axis, rotate θ about the y-axis in the direction of the positive x-axis and rotate φ about the z-axis in the direction of the positive y-axis.
Coordinate system conversions
As the spherical coordinate system is only one of many three-dimensional coordinate systems, there exist equations for converting coordinates between the spherical coordinate system and others.
Cartesian coordinate system
The three spherical coordinates are obtained from Cartesian coordinates by:
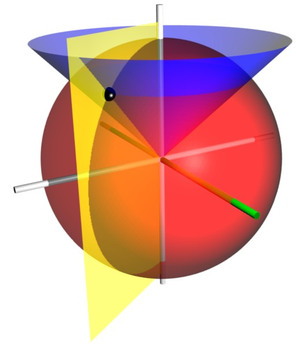
Note that the arctangent must be defined suitably so as to take account of the correct quadrant of 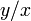 . The atan2 or equivalent function accomplishes this for computational purposes.
. The atan2 or equivalent function accomplishes this for computational purposes.
Conversely, Cartesian coordinates may be retrieved from spherical coordinates by:
Geographic coordinate system
The geographic coordinate system is an alternate version of the spherical coordinate system, used primarily in geography though also in mathematics and physics applications. In geography, ρ is usually dropped or replaced with a value representing elevation or altitude.
Latitude  is the complement of the zenith or colatitude, and can be converted by:
is the complement of the zenith or colatitude, and can be converted by:
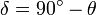 , or
, or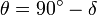 ,
,
though latitude is typically represented by θ as well. This represents a zenith angle originating from the xy-plane with a domain -90° ≤ θ ≤ 90°. The longitude is measured in degrees east or west from 0°, so its domain is -180° ≤ φ ≤ 180°.
Cylindrical coordinate system
The cylindrical coordinate system is a three-dimensional extrusion of the polar coordinate system, with an z coordinate to describe a point's height above or below the xy-plane. The full coordinate tuple is (r, φ, z).
Cylindrical coordinates may be converted into spherical coordinates by:
Spherical coordinates may be converted into cylindrical coordinates by:
Applications
The geographic coordinate system applies the two angles of the spherical coordinate system to express locations on Earth, calling them latitude and longitude. Just as the two-dimensional Cartesian coordinate system is useful on the plane, a two-dimensional spherical coordinate system is useful on the surface of a sphere. In this system, the sphere is taken as a unit sphere, so the radius is unity and can generally be ignored. This simplification can also be very useful when dealing with objects such as rotational matrices.
Spherical coordinates are useful in analyzing systems that are symmetrical about a point; a sphere that has the Cartesian equation x2 + y2 + z2 = c2 has the very simple equation r = c in spherical coordinates. An example is in solving a triple integral with a sphere as its domain.
The surface element for a spherical surface is
The volume element is
Spherical coordinates are the natural coordinates for describing and analyzing physical situations where there is spherical symmetry, such as the potential energy field surrounding a sphere (or point) with mass or charge. Two important partial differential equations, Laplace's equation and the Helmholtz equation, allow a separation of variables in spherical coordinates. The angular portions of the solutions to such equations take the form of spherical harmonics.
Another application is ergonomic design, where r is the arm length of a stationary person and the angles describe the direction of the arm as it reaches out.
The concept of spherical coordinates can be extended to higher dimensional spaces and are then referred to as hyperspherical coordinates.
Kinematics
In spherical coordinates the position of a point is written,
its velocity is then,
and its acceleration is,