Euclidean geometry
About this schools Wikipedia selection
SOS Children have produced a selection of wikipedia articles for schools since 2005. SOS Children is the world's largest charity giving orphaned and abandoned children the chance of family life.
Euclidean geometry is a mathematical system attributed to the Greek mathematician Euclid of Alexandria. Euclid's text Elements is the earliest known systematic discussion of geometry. It has been one of the most influential books in history, as much for its method as for its mathematical content. The method consists of assuming a small set of intuitively appealing axioms, and then proving many other propositions (theorems) from those axioms. Although many of Euclid's results had been stated by earlier Greek mathematicians, Euclid was the first to show how these propositions could be fit together into a comprehensive deductive and logical system.
The Elements begin with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. The Elements goes on to the solid geometry of three dimensions, and Euclidean geometry was subsequently extended to any finite number of dimensions. Much of the Elements states results of what is now called number theory, proved using geometrical methods.
For over two thousand years, the adjective "Euclidean" was unnecessary because no other sort of geometry had been conceived. Euclid's axioms seemed so intuitively obvious that any theorem proved from them was deemed true in an absolute sense. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. It also is no longer taken for granted that Euclidean geometry describes physical space. An implication of Einstein's theory of general relativity is that Euclidean geometry is only a good approximation to the properties of physical space if the gravitational field is not too strong.
Axiomatic approach
Euclidean geometry is an axiomatic system, in which all theorems ("true statements") are derived from a finite number of axioms. Near the beginning of the first book of the Elements, Euclid gives five postulates (axioms):
- Any two points can be joined by a straight line.
- Any straight line segment can be extended indefinitely in a straight line.
- Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as centre.
- All right angles are congruent.
- Parallel postulate. If two lines intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.
These axioms invoke the following concepts: point, straight line segment and line, side of a line, circle with radius and centre, right angle, congruence, inner and right angles, sum. The following verbs appear: join, extend, draw, intersect. The circle described in postulate 3 is tacitly unique. Postulates 3 and 5 hold only for plane geometry; in three dimensions, postulate 3 defines a sphere.

Postulate 5 leads to the same geometry as the following statement, known as Playfair's axiom, which also holds only in the plane:
Through a point not on a given straight line, one and only one line can be drawn that never meets the given line.
Postulates 1, 2, 3, and 5 assert the existence and uniqueness of certain geometric figures, and these assertions are of a constructive nature: that is, we are not only told that certain things exist, but are also given methods for creating them with no more than a compass and an unmarked straightedge. In this sense, Euclidean geometry is more concrete than many modern axiomatic systems such as set theory, which often assert the existence of objects without saying how to construct them, or even assert the existence of objects that cannot be constructed within the theory.
Strictly speaking, the constructs of lines on paper etc are models of the objects defined within the formal system, rather than instances of those objects. For example a Euclidean straight line has no width, but any real drawn line will.
The Elements also include the following five "common notions":
- Things that equal the same thing also equal one another.
- If equals are added to equals, then the wholes are equal.
- If equals are subtracted from equals, then the remainders are equal.
- Things that coincide with one another equal one another.
- The whole is greater than the part.
Euclid also invoked other properties pertaining to magnitudes. 1 is the only part of the underlying logic that Euclid explicitly articulated. 2 and 3 are "arithmetical" principles; note that the meanings of "add" and "subtract" in this purely geometric context are taken as given. 1 through 4 operationally define equality, which can also be taken as part of the underlying logic or as an equivalence relation requiring, like "coincide," careful prior definition. 5 is a principle of mereology. "Whole", "part", and "remainder" beg for precise definitions.
In the 19th century, it was realized that Euclid's ten axioms and common notions do not suffice to prove all of theorems stated in the Elements. For example, Euclid assumed implicitly that any line contains at least two points, but this assumption cannot be proved from the other axioms, and therefore needs to be an axiom itself. The very first geometric proof in the Elements, shown in the figure on the right, is that any line segment is part of a triangle; Euclid constructs this in the usual way, by drawing circles around both endpoints and taking their intersection as the third vertex. His axioms, however, do not guarantee that the circles actually intersect, because they are consistent with discrete, rather than continuous, space. Starting with Moritz Pasch in 1882, many improved axiomatic systems for geometry have been proposed, the best known being those of Hilbert, George Birkhoff, and Tarski.
To be fair to Euclid, the first formal logic capable of supporting his geometry was that of Frege's 1879 Begriffsschrift, little read until the 1950s. We now see that Euclidean geometry should be embedded in first-order logic with identity, a formal system first set out in Hilbert and Wilhelm Ackermann's 1928 Principles of Theoretical Logic. Formal mereology began only in 1916, with the work of Lesniewski and A. N. Whitehead. Tarski and his students did major work on the foundations of elementary geometry as recently as between 1959 and his death in 1983.
The parallel postulate
To the ancients, the parallel postulate seemed less obvious than the others; verifying it physically would require us to inspect two lines to check that they never intersected, even at some very distant point, and this inspection could potentially take an infinite amount of time. Euclid himself seems to have considered it as being qualitatively different from the others, as evidenced by the organization of the Elements: the first 28 propositions he presents are those that can be proved without it.
Many geometers tried in vain to prove the fifth postulate from the first four. By 1763 at least 28 different proofs had been published, but all were found to be incorrect. In fact the parallel postulate cannot be proved from the other four: this was shown in the 19th century by the construction of alternative ( non-Euclidean) systems of geometry where the other axioms are still true but the parallel postulate is replaced by a conflicting axiom. One distinguishing aspect of these systems is that the three angles of a triangle do not add to 180°: in hyperbolic geometry the sum of the three angles is always less than 180° and can approach zero, while in elliptic geometry it is greater than 180°. If the parallel postulate is dropped from the list of axioms without replacement, the result is the more general geometry called absolute geometry.
Treatment using analytic geometry
The development of analytic geometry provided an alternative method for formalizing geometry. In this approach, a point is represented by its Cartesian (x,y) coordinates, a line is represented by its equation, and so on. In the 20th century, this fit into David Hilbert's program of reducing all of mathematics to arithmetic, and then proving the consistency of arithmetic using finitistic reasoning. In Euclid's original approach, the Pythagorean theorem follows from Euclid's axioms. In the Cartesian approach, the axioms are the axioms of algebra, and the equation expressing the Pythagorean theorem is then a definition of one of the terms in Euclid's axioms, which are now considered to be theorems. The equation
defining the distance between two points 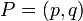 and
and 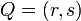 is then known as the Euclidean metric, and other metrics define non-Euclidean geometries.
is then known as the Euclidean metric, and other metrics define non-Euclidean geometries.
As a description of physical reality

Euclid believed that his axioms were self-evident statements about physical reality.
This led to deep philosophical difficulties in reconciling the status of knowledge from observation as opposed to knowledge gained by the action of thought and reasoning. A major investigation of this area was conducted by Immanuel Kant in The Critique of Pure Reason.
However, Einstein's theory of general relativity shows that the true geometry of spacetime is non-Euclidean geometry. For example, if a triangle is constructed out of three rays of light, then in general the interior angles do not add up to 180 degrees due to gravity. A relatively weak gravitational field, such as the Earth's or the sun's, is represented by a metric that is approximately, but not exactly, Euclidean. Until the 20th century, there was no technology capable of detecting the deviations from Euclidean geometry, but Einstein predicted that such deviations would exist. They were later verified by observations such as the observation of the slight bending of starlight by the Sun during a solar eclipse in 1919, and non-Euclidean geometry is now, for example, an integral part of the software that runs the GPS system. It is possible to object to the non-Euclidean interpretation of general relativity on the grounds that light rays might be improper physical models of Euclid's lines, or that relativity could be rephrased so as to avoid the geometrical interpretations. However, one of the consequences of Einstein's theory is that there is no possible physical test that can do any better than a beam of light as a model of geometry. Thus, the only logical possibilities are to accept non-Euclidean geometry as physically real, or to reject the entire notion of physical tests of the axioms of geometry, which can then be imagined as a formal system without any intrinsic real-world meaning.
Because of the incompatibility of the Standard Model with general relativity, and because of some recent empirical evidence against the former, both theories are now under increased scrutiny, and many theories have been proposed to replace the former and, in many cases, the latter as well. ( GUTs are the only example of post-Standard Model theories that do not tackle general relativity.) The disagreements between the two theories come from their claims about space-time, and it is now accepted that physical geometry must describe space-time rather than merely space. While Euclidean geometry, the Standard Model and general relativity are all compatible with any number of spatial dimensions and any specification as to which of these if any are compactified (see string theory), and while all bar Euclidean geometry (which does not distinguish space from time) insist on exactly one temporal dimension, proposed alternatives, none of which are yet part of scientific consensus, differ significantly in their predictions or lack thereof as to these details of space-time. The disagreements between the conventional physical theories concern whether space-time is Euclidean (since quantum field theory in the standard model is built on the assumption that it is) and on whether it is quantized. Few if any proposed alternatives deny that space-time is quantized, with the quanta of length and time are respectively the Planck length and the Planck time. However, which geometry to use - Euclidean, Riemannian, de Stitter, anti de Stitter and some others - is a major point of demarcation between them. Many physicists expect some Euclidean string theory to eventually become the Theory Of Everything, but their view is by no means unanimous, and in any case the future of this issue is unpredictable. Regarding how if at all Euclidean geometry will be involved in future physics, what is uncontroversial is that the definition of straight lines will still be in terms of the path in a vacuum of electromagnetic radiation (including light) until gravity is explained with mathematical consistency in terms of a phenomenon other than space-time curvature, and that the test of geometrical postulates (Euclidean or otherwise) will lie in studying how these paths are affected by phenomena. For now, gravity is the only known relevant phenomenon, and its effect is uncontroversial (see gravitational lensing).
Conic sections and gravitational theory
Apollonius and other Ancient Greek geometers made an extensive study of the conic sections — curves created by intersecting a cone and a plane. The (nondegenerate) ones are the ellipse, the parabola and the hyperbola, distinguished by having zero, one, or two intersections with infinity. This turned out to facilitate the work of Galileo, Kepler and Newton in the 17th Century, as these curves accurately modeled the movement of bodies under the influence of gravity. Using Newton's law of universal gravitation, the orbit of a comet around the Sun is
- an ellipse, if it is moving too slowly for its position (below escape velocity), in which case it will eventually return;
- a parabola, if it is moving with exact escape velocity (unlikely), and will never return because the curve reaches to infinity; or
- a hyperbola, if it is moving fast enough (above escape velocity), and likewise will never return.
In each case the Sun will be at one focus of the conic, and the motion will sweep out equal areas in equal times.
Galileo experimented with objects falling small distances at the surface of the Earth, and empirically determined that the distance travelled was proportional to the square of the time. Given his timing and measuring apparatus, this was an excellent approximation. Over such small distances that the acceleration of gravity can be considered constant, and ignoring the effects of air (as on a falling feather) and the rotation of the Earth, the trajectory of a projectile will be a parabolic path.
Later calculations of these paths for bodies moving under gravity would be performed using the techniques of analytical geometry (using coordinates and algebra) and differential calculus, which provide straightforward proofs. Of course these techniques had not been invented at the time that Galileo investigated the movement of falling bodies. Once he found that bodies fall to the earth with constant acceleration (within the accuracy of his methods), he proved that projectiles will move in a parabolic path using the procedures of Euclidean geometry.
Similarly, Newton used quasi–Euclidean proofs to demonstrate the derivation of Keplerian orbital movements from his laws of motion and gravitation.
Centuries later, one of the first experimental measurements to support Einstein's general theory of relativity, which postulated a non-Euclidean geometry for space, was the orbit of the planet Mercury. Kepler described the orbit as a perfect ellipse. Newtonian theory predicted that the gravitational influence of other bodies would give a more complicated orbit. But eventually all such Newtonian corrections fell short of experimental results; a small perturbation remained. Einstein postulated that the bending of space would precisely account for that perturbation.
Logical status
Euclidean geometry is a first-order theory. That is, it allows statements such as those that begin as "for all triangles ...", but it is incapable of forming statements such as "for all sets of triangles ...". Statements of the latter type are deemed to be outside the scope of the theory.
We owe much of our present understanding of the properties of the logical and metamathematical properties of Euclidean geometry to the work of Alfred Tarski and his students, beginning in the 1920s. Tarski proved his axiomatic formulation of Euclidean geometry to be complete in a certain sense: there is an algorithm which, for every proposition, can show it to be either true or false. Gödel's incompleteness theorems showed the futility of Hilbert's program of proving the consistency of all of mathematics using finitistic reasoning. Tarski's findings do not violate Gödel's theorem, because Euclidean geometry cannot describe a sufficient amount of arithmetic for the theorem to apply.
Although complete in the formal sense used in modern logic, there are things that Euclidean geometry cannot accomplish. For example, the problem of trisecting an angle with a compass and straightedge is one that naturally occurs within the theory, since the axioms refer to constructive operations that can be carried out with those tools. However, centuries of efforts failed to find a solution to this problem, until Pierre Wantzel published a proof in 1837 that such a construction was impossible.
Absolute geometry, first identified by Bolyai, is Euclidean geometry weakened by omission of the fifth postulate, that parallel lines do not meet. Of strength intermediate between absolute geometry and Euclidean are geometries derived from Euclid's by alterations of the parallel postulate that can be shown to be consistent by exhibiting models of them. For example, geometry on the surface of a sphere is a model of elliptical geometry. Another weakening of Euclidean geometry is affine geometry, first identified by Euler, which retains the fifth postulate unmodified while weakening postulates three and four in a way that eliminates the notions of angle (whence right triangles become meaningless) and of equality of length of line segments in general (whence circles become meaningless) while retaining the notions of parallelism as an equivalence relation between lines, and equality of length of parallel line segments (so line segments continue to have a midpoint).
Classical theorems
- Ceva's theorem
- Heron's formula
- Nine-point circle
- Pythagorean theorem
- Tartaglia's formula
- Menelaus's theorem
- Angle bisector theorem