
Mathematical proof
Background Information
Arranging a Wikipedia selection for schools in the developing world without internet was an initiative by SOS Children. With SOS Children you can choose to sponsor children in over a hundred countries
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true, within the accepted standards of the field. A proof is a logical argument, not an empirical one. That is, the proof must demonstrate that a proposition is true in all cases to which it applies, without a single exception. An unproven proposition believed or strongly suspected to be true is known as a conjecture.
Proofs employ logic but usually include some amount of natural language which usually admits some ambiguity. In fact, the vast majority of proofs in written mathematics can be considered as applications of informal logic. Purely formal proofs are considered in proof theory. The distinction between formal and informal proofs has led to much examination of current and historical mathematical practice, quasi-empiricism in mathematics, and so-called folk mathematics (in both senses of that term). The philosophy of mathematics is concerned with the role of language and logic in proofs, and mathematics as a language.
Regardless of one's attitude to formalism, the result that is proved to be true is a theorem; in a completely formal proof it would be the final line, and the complete proof shows how it follows from the axioms alone by the application of the rules of inference. Once a theorem is proved, it can be used as the basis to prove further statements. A theorem may also be referred to as a lemma if it is used as a stepping stone in the proof of a theorem. The axioms are those statements one cannot, or need not, prove. These were once the primary study of philosophers of mathematics. Today focus is more on practice, i.e. acceptable techniques.
Methods of proof
Direct proof
In direct proof, the conclusion is established by logically combining the axioms, definitions, and earlier theorems. For example, direct proof can be used to establish that the sum of two even integers is always even:
- For any two even integers
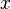 and
and 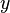 we can write
we can write  and
and  for some integers
for some integers 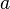 and
and 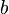 , since both
, since both 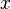 and
and 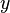 are multiples of 2. But the sum
are multiples of 2. But the sum 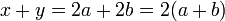 is also a multiple of 2, so it is therefore even by definition.
is also a multiple of 2, so it is therefore even by definition.
This proof uses definition of even integers, as well as distribution law.
Proof by induction
In proof by induction, first a "base case" is proved, and then an "induction rule" is used to prove a (often infinite) series of other cases. Since the base case is true, the infinity of other cases must also be true, even if all of them cannot be proved directly because of their infinite number. A subset of induction is Infinite descent. Infinite descent can be used to prove the irrationality of the square root of two.
The principle of mathematical induction states that: Let N = { 1, 2, 3, 4, ... } be the set of natural numbers and P(n) be a mathematical statement involving the natural number n belonging to N such that (i) P(1) is true, ie, P(n) is true for n = 1 (ii) P(m + 1) is true whenever P(m) is true, ie, P(m) is true implies that P(m + 1) is true. Then P(n) is true for the set of natural numbers N.
Proof by transposition
Proof by Transposition establishes the conclusion "if p then q" by proving the equivalent contrapositive statement "if not q then not p".
Proof by contradiction
In proof by contradiction (also known as reductio ad absurdum, Latin for "reduction into the absurd"), it is shown that if some statement were false, a logical contradiction occurs, hence the statement must be true. This method is perhaps the most prevalent of mathematical proofs. A famous example of a proof by contradiction shows that 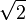 is irrational:
is irrational:
- Suppose that
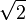 is rational, so
is rational, so 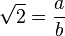 where a and b are non-zero integers with no common factor (definition of rational number). Thus,
where a and b are non-zero integers with no common factor (definition of rational number). Thus, 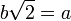 . Squaring both sides yields 2b2 = a2. Since 2 divides the left hand side, 2 must also divide the right hand side (as they are equal and both integers). So a2 is even, which implies that a must also be even. So we can write a = 2c, where c is also an integer. Substitution into the original equation yields 2b2 = (2c)2 = 4c2. Dividing both sides by 2 yields b2 = 2c2. But then, by the same argument as before, 2 divides b2, so b must be even. However, if a and b are both even, they share a factor, namely 2. This contradicts our assumption, so we are forced to conclude that
. Squaring both sides yields 2b2 = a2. Since 2 divides the left hand side, 2 must also divide the right hand side (as they are equal and both integers). So a2 is even, which implies that a must also be even. So we can write a = 2c, where c is also an integer. Substitution into the original equation yields 2b2 = (2c)2 = 4c2. Dividing both sides by 2 yields b2 = 2c2. But then, by the same argument as before, 2 divides b2, so b must be even. However, if a and b are both even, they share a factor, namely 2. This contradicts our assumption, so we are forced to conclude that 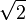 is irrational.
is irrational.
Proof by construction
Proof by construction, or proof by example, is the construction of a concrete example with a property to show that something having that property exists. Joseph Liouville, for instance, proved the existence of transcendental numbers by constructing an explicit example.
Proof by exhaustion
In Proof by exhaustion, the conclusion is established by dividing it into a finite number of cases and proving each one separately. The number of cases sometimes can become very large. For example, the first proof of the four colour theorem was a proof by exhaustion with 1,936 cases. This proof was controversial because the majority of the cases were checked by a computer program, not by hand. The shortest known proof of the four colour theorem today still has over 600 cases.
Probabilistic proof
A probabilistic proof is one in which an example is shown to exist, with certainty, by using methods of probability theory. This is not be confused with an argument that a theorem is 'probably' true. The latter type of reasoning can be called a 'plausibility argument' and is not a proof; in the case of the Collatz conjecture it is clear how far that is from a genuine proof. Probabilistic proof, like proof by construction, is one of many ways to show existence theorems.
Combinatorial proof
A combinatorial proof establishes the equivalence of different expressions by showing that they count the same object in different ways. Usually a bijection is used to show that the two interpretations give the same result.
Nonconstructive proof
A nonconstructive proof establishes that a certain mathematical object must exist (e.g. "Some X satisfies f(X)"), without explaining how such an object can be found. Often, this takes the form of a proof by contradiction in which the nonexistence of the object is proven to be impossible. In contrast, a constructive proof establishes that a particular object exists by providing a method of finding it. A famous example of a nonconstructive proof shows that there exist two irrational numbers 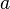 and
and 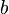 such that
such that 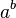 is a rational number:
is a rational number:
- Either
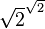 is a rational number and we are done (take
is a rational number and we are done (take 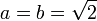 ), or
), or 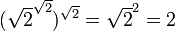 shows that we can take
shows that we can take 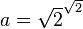 and
and 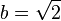 .
.
Proof nor disproof
There is a class of mathematical statements for which neither a proof nor disproof exists, using only ZFC, the standard form of axiomatic set theory. Examples include the continuum hypothesis; see further List of statements undecidable in ZFC. Under the assumption that ZFC is consistent, the existence of such statements follows from Gödel's (first) incompleteness theorem. Whether a particular unproven proposition can be proved or disproved using a standard set of axioms is not always obvious, and can be extremely technical to determine. To show that a mathematical statement is independent (or undecidable) in a given formalization of mathematics such as ZFC requires methods that transcend the given formalization.
Elementary proof
An elementary proof is (usually) a proof which does not use complex analysis. For some time it was thought that certain theorems, like the prime number theorem, could only be proved using "higher" mathematics. However, over time, many of these results have been reproved using only elementary techniques.
End of a proof
Sometimes, the abbreviation "Q.E.D." is written to indicate the end of a proof. This abbreviation stands for "Quod Erat Demonstrandum", which is Latin for "that which was to be demonstrated". An alternative is to use a square or a rectangle, such as □ or ∎, known as a " tombstone" or "halmos".
