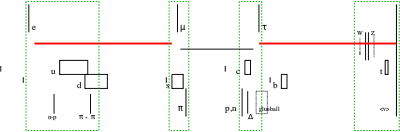
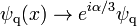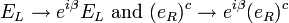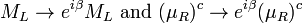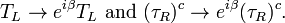Standard Model

Background Information

SOS Children produced this website for schools as well as this video website about Africa. SOS Children is the world's largest charity giving orphaned and abandoned children the chance of family life.

Quantum field theory
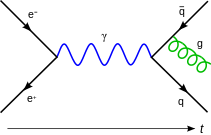Feynman diagram
History
Background Field theory Gauge theory Poincaré symmetry Quantum mechanics Spontaneous symmetry breaking
Symmetries Charge conjugation Crossing Parity Time reversal
Tools Anomaly Effective field theory Expectation value Faddeev–Popov ghosts Feynman diagram Lattice gauge theory LSZ reduction formula Partition function Propagator Quantization Regularization Renormalization Vacuum state Wick's theorem Wightman axioms
Equations Dirac equation Klein–Gordon equation Proca equations Wheeler–DeWitt equation Bargmann–Wigner equations
Standard Model Electroweak interaction Higgs mechanism Quantum chromodynamics Quantum electrodynamics Yang–Mills theory
Incomplete theories Quantum gravity String theory Supersymmetry Technicolor Theory of everything
Scientists C. D. Anderson P. W. Anderson Bardeen Bethe Bjorken Bogoliubov Brout Cabibbo Callan Cronin DeWitt Dirac Dyson Englert Fermi Feynman Fierz Fisher Fock Fröhlich Gell-Mann Gross Hänsch Heisenberg Higgs Haag 't Hooft Kadanoff Kendall Klitzing Kobayashi Lamb Landau Lee Majorana Maskawa Mills Nambu Nishijima Parisi Paul Polyakov Salam Schwinger Shockley Skyrme Störmer Sudarshan Thomson Tomonaga Veltman Ward Weinberg Wilczek Wilson Yang Yukawa

The Standard Model of particle physics is a theory that describes three of the four known fundamental interactions among the elementary particles that make up all matter. It groups the electroweak theory and quantum chromodynamics into a structure denoted by the gauge group SU(3)×SU(2)×U(1). It is a relativistic quantum field theory which is consistent with both quantum mechanics and special relativity. To date, almost all experimental tests of the three forces described by the Standard Model have agreed with its predictions.

The Standard Model falls short of being a complete theory of fundamental interactions, primarily because of its lack of inclusion of gravity, the fourth known fundamental interaction, and also because of the recent observation of neutrino oscillations.

Historical background

The formulation of the unification of the electromagnetic and weak interactions in the Standard Model is due to Steven Weinberg, Abdus Salam and, subsequently, Sheldon Glashow. The unification model was initially proposed by Steven Weinberg in 1967, and completed integrating it with the proposal by Peter Higgs of spontaneous symmetry breaking which gives origin to the masses of all particles described in the model.

After the discovery, made at CERN of the existence of neutral weak currents, mediated by the Z boson, foreseen in the Standard Model, Glashow, Salam, and Weinberg received the Nobel Prize in physics in 1979.

Overview

In physics, the dynamics of both matter and energy in nature is presently best understood in terms of the kinematics and interactions of fundamental particles. To date, science has managed to reduce the laws which seem to govern the behavior and interaction of all types of matter and energy we are aware of, to a small core of fundamental laws and theories. A major goal of physics is to find the 'common ground' that would unite all of these into one integrated model of everything, in which all the other laws we know of would be special cases, and from which the behaviour of all matter and energy can be derived (at least in principle). "Details can be worked out if the situation is simple enough for us to make an approximation, which is almost never, but often we can understand more or less what is happening." ( Feynman's lectures on Physics, Vol 1. 2–7)

The standard model is a grouping of two major theories — quantum electroweak and quantum chromodynamics — which provides an internally consistent theory describing interactions between all experimentally observed particles. Technically, quantum field theory provides the mathematical framework for the standard model. The standard model describes each type of particle in terms of a mathematical field. For a technical description of the fields and their interactions, see standard model (mathematical formulation).

Particle Content

Particles in physics

Elementary

Fermions

Quarks	u u d d c c s s t t b b

Leptons	e− e+ μ− * μ+ τ− * τ+ ν e * ν e ν μ * ν μ ν τ * ν τ

Bosons

Gauge	γ g W± * Z

Scalar	H0

Others

Ghosts

Hypothetical

Superpartners

Gauginos	Gluino Gravitino

Others	Axino Chargino Higgsino Neutralino Sfermion

Others

A⁰
Dilaton
G
J
Majorana fermion
m
Tachyon
X
Y
W'
Z'
Sterile neutrino

Composite

Hadrons

Baryons / Hyperons	N p n Δ Λ Σ Ξ Ω

Mesons / Quarkonia	π ρ η η′ φ ω J/ψ ϒ θ K B D T

Others

Atomic nuclei
Atoms
Diquarks
Exotic atoms
- Positronium
- Muonium
- Tauonium
- Onia
Superatoms
Molecules

Hypothetical

Exotic hadrons

Exotic baryons	Dibaryon Pentaquark Skyrmion

Exotic mesons	Glueball Tetraquark

Others

Mesonic molecule
Pomeron

Quasiparticles

Davydov soliton
Exciton
Hole
Magnon
Phonon
Plasmaron
Plasmon
Polariton
Polaron
Roton
Trion

Lists

Baryons
Mesons
Particles
Quasiparticles
Timeline of particle discoveries

Wikipedia books

Hadronic Matter
Particles of the Standard Model
Leptons
Quarks

Physics portal

The particles of the standard model are organized into three classes according to their spin: fermions (spin-½ particles of matter), gauge bosons (spin-1 force-mediating particles), and the (spin-0) Higgs boson.

Particles of matter

All fermions in the Standard Model are spin-½, and follow the Pauli Exclusion Principle in accordance with the spin-statistics theorem.

Organization of Fermions
	Generation 1		Generation 2		Generation 3
Quarks	Up	u	Charm	c	Top	t
Quarks	Down	d	Strange	s	Bottom	b
Leptons	Electron Neutrino	ν e	Muon Neutrino	ν μ	Tau Neutrino	ν τ
Leptons	Electron	e−	Muon	μ−	Tau	τ−

Apart from their antiparticle partners, a total of twelve different fermions are known and accounted for. They are classified according to how they interact (or equivalently, what charges they carry): six of them are classified as quarks ( up, down, charm, strange, top, bottom), and the other six as leptons (electron, muon, tau, and their corresponding neutrinos).

Pairs from each classification are grouped together to form a generation, with corresponding particles exhibiting similar physical behaviour (see table of fermions).

The defining property of the quarks is that they carry colour charge, and hence, interact via the strong force. The infrared confining behavior of the strong force results in the quarks being perpetually bound to one another forming colour-neutral composite particles ( hadrons) of either two quarks ( mesons) or three quarks ( baryons). The familiar proton and the neutron are examples of the two lightest baryons. Quarks also carry electric charges and weak isospin. Hence they interact with other fermions electromagnetically and via the weak nuclear interactions.

The remaining six fermions that do not carry colour charge are defined to be the leptons. The three neutrinos do not carry electric charge either, so their motion is directly influenced only by means of the weak nuclear force. For this reason neutrinos are notoriously difficult to detect in laboratories. However, the electron, muon and the tau lepton carry an electric charge so they interact electromagnetically, too.

The Higgs boson

The Higgs particle is a hypothetical massive scalar elementary particle predicted by the Standard Model, and the only fundamental particle predicted by that model which has not been directly observed as yet. This is because it requires an exceptionally large amount of energy and beam luminosity to create and observe at high energy colliders. It has no intrinsic spin, and thus, (like the force mediating particles, which also have integral spin) is also classified as a boson.

The Higgs boson plays a unique role in the Standard Model, and a key role in explaining the origins of the mass of other elementary particles, in particular the difference between the massless photon and the very heavy W and Z bosons. Elementary particle masses, and the differences between electromagnetism (caused by the photon) and the weak force (caused by the W and Z bosons), are critical to many aspects of the structure of microscopic (and hence macroscopic) matter. In electroweak theory it generates the masses of the massive leptons (electron, muon and tau); and also of the quarks.

As of 2007, no experiment has directly detected the existence of the Higgs boson, but there is some indirect evidence for it. It is hoped that upon the completion of the Large Hadron Collider, experiments conducted at CERN would bring experimental evidence confirming the existence of the particle.

Science, a journal of original scientific research, has reported: "...experimenters may have already overlooked a Higgs particle, argues theorist Chien-Peng Yuan of Michigan State University in East Lansing and his colleagues. They considered the simplest possible supersymmetric theory. Ordinarily, theorists assume that the lightest of theory's five Higgses is the one that drags on the W and Z. Those interactions then feed back on Higgs and push its mass above 121 times the mass of the proton, the highest mass searched for at CERN's Large Electron–Positron (LEP) collider, which ran from 1989 to 2000. But it's possible that the lightest Higgs weighs as little as 65 times the mass of a proton and has been missed, Yuan and colleagues argue in a paper to be published in Physical Review Letters`."

Theoretical Aspects

Construction of the Standard Model Lagrangian

Parameters of the Standard Model
Symbol	Description	Renormalization scheme (point)	Value
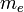$m_e$	Electron mass		511 keV
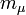$m_\mu$	Muon mass		106 MeV
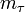$m_\tau$	Tau lepton mass		1.78 GeV
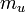$m_u$	Up quark mass	(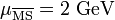 $\mu_{\overline{\text{MS}}}=2\text{ GeV}$ )	1.9 MeV
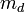$m_d$	Down quark mass	(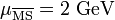 $\mu_{\overline{\text{MS}}}=2\text{ GeV}$ )	4.4 MeV
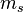$m_s$	Strange quark mass	(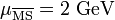 $\mu_{\overline{\text{MS}}}=2\text{ GeV}$ )	87 MeV
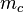$m_c$	Charm quark mass	(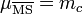 $\mu_{\overline{\text{MS}}}=m_c$ )	1.32 GeV
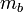$m_b$	Bottom quark mass	(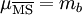 $\mu_{\overline{\text{MS}}}=m_b$ )	4.24 GeV
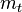$m_t$	Top quark mass	(on-shell scheme)	172.7 GeV
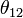$\theta_{12}$	CKM 12-mixing angle		0.229
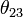$\theta_{23}$	CKM 23-mixing angle		0.042
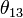$\theta_{13}$	CKM 13-mixing angle		0.004
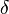$\delta$	CKM CP-Violating Phase		0.995
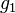$g_1$	U(1) gauge coupling	(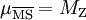 $\mu_{\overline{\text{MS}}}=M_\text{Z}$ )	0.357
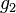$g_2$	SU(2) gauge coupling	(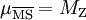 $\mu_{\overline{\text{MS}}}=M_\text{Z}$ )	0.652
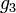$g_3$	SU(3) gauge coupling	(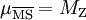 $\mu_{\overline{\text{MS}}}=M_\text{Z}$ )	1.221
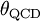$\theta_\text{QCD}$	QCD Vacuum Angle		~0
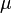$\mu$	Higgs quadratic coupling		Unknown
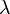$\lambda$	Higgs self-coupling strength		Unknown

Technically, quantum field theory provides the mathematical framework for the standard model, in which a Lagrangian controls the dynamics and kinematics of the theory. Each kind of particle is described in terms of a dynamical field that pervades space-time. The construction of the standard model proceeds following the modern method of constructing most field theories: by first postulating a set of symmetries of the system, and then by writing down the most general renormalizable Lagrangian from its particle (field) content that observes these symmetries.

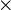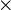The global Poincaré symmetry is postulated for all relativistic quantum field theories. It consists of the familiar translational symmetry, rotational symmetry and the inertial reference frame invariance central to the theory of special relativity. The local SU(3) $\times$ SU(2) $\times$ U(1) gauge symmetry is an internal symmetry that essentially defines the standard model. Roughly, the three factors of the gauge symmetry give rise to the three fundamental interactions. The fields fall into different representations of the various symmetry groups of the Standard Model (see table). Upon writing the most general Lagrangian, one finds that the dynamics depend on 19 parameters, whose numerical values are established by experiment. The parameters are summarized in the table at right.

Additional Symmetries of the Standard Model

From the theoretical point of view, the standard model exhibits additional global symmetries that were not posulated at the outset of its construction. There are four such symmetries and are collectively called accidental symmetries, all of which are continuous U(1) global symmetries. The transformations leaving the Lagrangian invariant are

$\psi_\text{q}(x)\rightarrow e^{i\alpha/3}\psi_\text{q}$

$E_L\rightarrow e^{i\beta}E_L\text{ and }(e_R)^c\rightarrow e^{i\beta}(e_R)^c$

$M_L\rightarrow e^{i\beta}M_L\text{ and }(\mu_R)^c\rightarrow e^{i\beta}(\mu_R)^c$

$T_L\rightarrow e^{i\beta}T_L\text{ and }(\tau_R)^c\rightarrow e^{i\beta}(\tau_R)^c.$

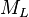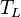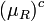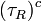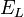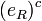The first transformation rule is shorthand to mean that all quark fields for all generations must be rotated by an identical phase simultaneously. The fields $M_L$ , $T_L$ and $(\mu_R)^c$ , $(\tau_R)^c$ are the 2nd (muon)and 3rd (tau) generation analogs of $E_L$ and $(e_R)^c$ fields.

By Noether's theorem, each of these symmetries yields an associated conservation law. They are the conservation of baryon number, electron number, muon number, and tau number. Each quark carries 1/3 of a baryon number, while each antiquark carries -1/3 of a baryon number. The conservation law implies that the total number of quarks minus number of antiquarks stays constant throughout time. Within experimental limits, no violation of this conservation law has been found.

Similarly, each electron and its associated neutrino carries +1 electron number, while the antielectron and the associated antineutrino carry -1 electron number, the muons carry +1 muon number and the tau leptons carry +1 tau number. The standard model predicts that each of these three numbers should be conserved separately in a manner similar to the baryon number. These numbers are collectively known as lepton family numbers (LF). The difference in the symmetry structures between the quark and the lepton sectors is due to the masslessness of neutrinos in the standard model. However, it was recently found that neutrinos have small mass, and oscillate between flavours, signaling the violation of these three quantum numbers.

In addition to the accidental (but exact) symmetries described above, the standard model exhibits a set of approximate symmetries. These are the SU(2) Custodial Symmetry and the SU(2) or SU(3) quark flavor symmetry.

Symmetries of the Standard Model and Associated Conservation Laws
Symmetry	Lie Group	Symmetry Type	Conservation Law
Poincaré	Translations 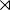$\rtimes$ SO(3,1)	Global symmetry	Energy, Momentum, Angular Momentum
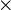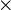Gauge	SU(3) $\times$ SU(2) $\times$ U(1)	Local symmetry	Electric charge, Weak isospin, Colour charge
Baryon phase	U(1)	Accidental Global symmetry	Baryon number
Electron phase	U(1)	Accidental Global symmetry	Electron number
Muon phase	U(1)	Accidental Global symmetry	Muon number
Tau phase	U(1)	Accidental Global symmetry	Tau-lepton number

Field content of the Standard Model
Field (1st generation)		Spin	Gauge Group Representation	Baryon Number	Electron Number
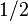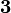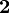Left-handed quark	$Q_\text{L}$	$1/2$	( $\mathbf{3}$ , $\mathbf{2}$ , $+1/6$ )	$1/3$	$0$
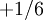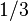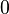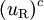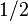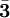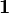Right-handed up quark	$(u_\text{R})^c$	$1/2$	( $\bar\mathbf{3}$ , $\mathbf{1}$ , $-2/3$ )	$-1/3$	$0$
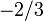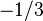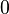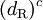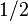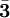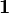Right-handed down quark	$(d_\text{R})^c$	$1/2$	( $\bar\mathbf{3}$ , $\mathbf{1}$ , $+1/3$ )	$-1/3$	$0$
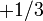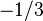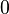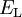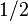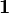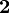Left-handed lepton	$E_\text{L}$	$1/2$	( $\mathbf{1}$ , $\mathbf{2}$ , $-1/2$ )	$0$	$1$
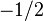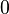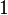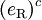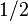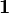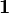Right-handed electron	$(e_\text{R})^c$	$1/2$	( $\mathbf{1}$ , $\mathbf{1}$ , $+1$ )	$0$	$-1$
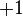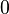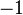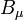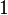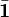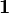Hypercharge gauge field	$B_\mu$	$1$	( $\bar\mathbf{1}$ , $\mathbf{1}$ , $0$ )	$0$	$0$
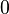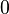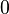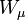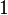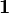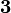Isospin gauge field	$W_\mu$	$1$	( $\mathbf{1}$ , $\mathbf{3}$ , $0$ )	$0$	$0$
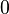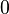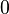Gluon field	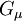$G_\mu$	$1$	( $\mathbf{8}$ , $\mathbf{1}$ , $0$ )	$0$	$0$
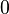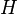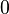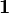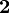Higgs field	$H$	$0$	( $\mathbf{1}$ , $\mathbf{2}$ , $+1/2$ )	$0$	$0$

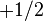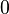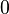List of standard model fermions

This table is based in part on data gathered by the Particle Data Group ( Quarks PDF (54.8 KB)).

**Left-handed fermions in the Standard Model**
Generation 1
Fermion (left-handed)	Symbol	Electric charge	Weak isospin	Weak hypercharge	Colour charge *	Mass **
Electron	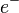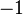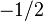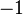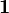$e^-\,$	$-1\,$	$-1/2\,$	$-1\,$	$\bold{1}\,$	511 keV
Positron	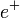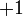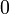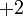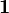$e^+\,$	$+1\,$	$0\,$	$+2\,$	$\bold{1}\,$	511 keV
Electron-neutrino	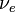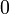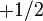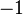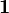$\nu_e\,$	$0\,$	$+1/2\,$	$-1\,$	$\bold{1}\,$	< 2 eV ****
Up quark	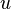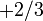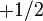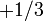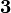$u\,$	$+2/3\,$	$+1/2\,$	$+1/3\,$	$\bold{3}\,$	~ 3 MeV ***
Up antiquark	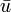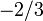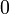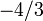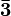$\bar{u}\,$	$-2/3\,$	$0\,$	$-4/3\,$	$\bold{\bar{3}}\,$	~ 3 MeV ***
Down quark	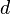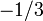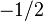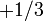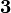$d\,$	$-1/3\,$	$-1/2\,$	$+1/3\,$	$\bold{3}\,$	~ 6 MeV ***
Down antiquark	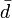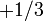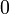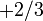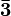$\bar{d}\,$	$+1/3\,$	$0\,$	$+2/3\,$	$\bold{\bar{3}}\,$	~ 6 MeV ***

Generation 2
Fermion (left-handed)	Symbol	Electric charge	Weak isospin	Weak hypercharge	Colour charge *	Mass **
Muon	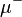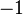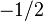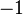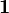$\mu^-\,$	$-1\,$	$-1/2\,$	$-1\,$	$\bold{1}\,$	106 MeV
Antimuon	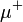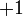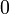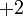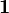$\mu^+\,$	$+1\,$	$0\,$	$+2\,$	$\bold{1}\,$	106 MeV
Muon-neutrino	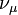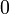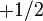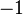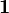$\nu_\mu\,$	$0\,$	$+1/2\,$	$-1\,$	$\bold{1}\,$	< 2 eV ****
Charm quark	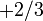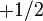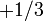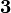$c\,$	$+2/3\,$	$+1/2\,$	$+1/3\,$	$\bold{3}\,$	~ 1.3 GeV
Charm antiquark	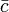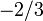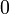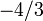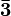$\bar{c}\,$	$-2/3\,$	$0\,$	$-4/3\,$	$\bold{\bar{3}}\,$	~ 1.3 GeV
Strange quark	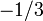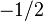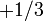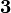$s\,$	$-1/3\,$	$-1/2\,$	$+1/3\,$	$\bold{3}\,$	~ 100 MeV
Strange antiquark	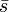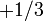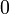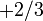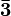$\bar{s}\,$	$+1/3\,$	$0\,$	$+2/3\,$	$\bold{\bar{3}}\,$	~ 100 MeV

Generation 3
Fermion (left-handed)	Symbol	Electric charge	Weak isospin	Weak hypercharge	Colour charge *	Mass **
Tau lepton	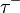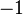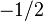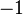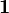$\tau^-\,$	$-1\,$	$-1/2\,$	$-1\,$	$\bold{1}\,$	1.78 GeV
Anti-tau lepton	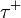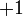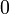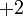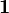$\tau^+\,$	$+1\,$	$0\,$	$+2\,$	$\bold{1}\,$	1.78 GeV
Tau-neutrino	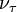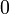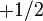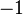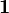$\nu_\tau\,$	$0\,$	$+1/2\,$	$-1\,$	$\bold{1}\,$	< 2 eV ****
Top quark	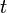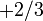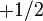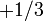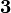$t\,$	$+2/3\,$	$+1/2\,$	$+1/3\,$	$\bold{3}\,$	171 GeV
Top antiquark	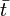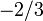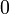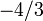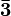$\bar{t}\,$	$-2/3\,$	$0\,$	$-4/3\,$	$\bold{\bar{3}}\,$	171 GeV
Bottom quark	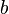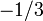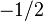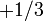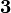$b\,$	$-1/3\,$	$-1/2\,$	$+1/3\,$	$\bold{3}\,$	~ 4.2 GeV
Bottom antiquark	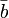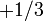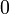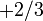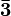$\bar{b}\,$	$+1/3\,$	$0\,$	$+2/3\,$	$\bold{\bar{3}}\,$	~ 4.2 GeV
Notes: * These are not ordinary abelian charges, which can be added together, but are labels of group representations of Lie groups. Mass is really a coupling between a left-handed fermion and a right-handed fermion. For example, the mass of an electron is really a coupling between a left-handed electron and a right-handed electron, which is the antiparticle of a left-handed positron. Also neutrinos show large mixings in their mass coupling, so it's not accurate to talk about neutrino masses in the flavor basis or to suggest a left-handed electron antineutrino. *** The masses of baryons and hadrons and various cross-sections are the experimentally measured quantities. Since quarks can't be isolated because of QCD confinement, the quantity here is supposed to be the mass of the quark at the renormalization scale of the QCD scale. ****** The Standard Model assumes that neutrinos are massless. However, several contemporary experiments prove that neutrinos oscillate between their flavour states, which could not happen if all were massless. It is straightforward to extend the model to fit these data but there are many possibilities, so the mass eigenstates are still open. See Neutrino#Mass.

Log plot of masses in the Standard Model.

Tests and predictions

The Standard Model predicted the existence of W and Z bosons, the gluon, the top quark and the charm quark before these particles had been observed. Their predicted properties were experimentally confirmed with good precision.

The Large Electron-Positron Collider at CERN tested various predictions about the decay of Z bosons, and found them confirmed.

To get an idea of the success of the Standard Model a comparison between the measured and the predicted values of some quantities are shown in the following table:

Quantity	Measured (GeV)	SM prediction (GeV)
Mass of W boson	80.398±0.025	80.3900±0.0180
Mass of Z boson	91.1876±0.0021	91.1874±0.0021

Challenges to the standard model

List of unsolved problems in physics
Parameters in the Standard Model: What gives rise to the Standard Model of particle physics? Why do its particle masses and coupling constants possess the values we have measured? Does the Higgs boson predicted by the model really exist? Why are there three generations of particles in the Standard Model?

The Standard Model of particle physics has been empirically determined through experiments over the past fifty years. Currently the Standard Model predicts that there is one more particle to be discovered, the Higgs boson. One of the reasons for building the Large Hadron Collider is that the increase in energy is expected to make the Higgs observable. However, as of 2007, there are only indirect experimental indications for the existence of the Higgs boson and it can not be claimed to be found.

There has been a great deal of both theoretical and experimental research exploring whether the Standard Model could be extended into a complete theory of everything. This area of research is often described by the term ' Beyond the Standard Model'. There are several motivations for this research. First, the Standard Model does not attempt to explain gravity, and it is unknown how to combine quantum field theory which is used for the Standard Model with general relativity which is the best physical model of gravity. This means that there is not a good theoretical model for phenomena such as the early universe.

Another avenue of research is related to the fact that the standard model seems very ad-hoc and inelegant. For example, the theory contains many seemingly so unrelated parameters of the theory — 21 in all (18 parameters in the core theory, plus G, c and h; there are believed to be an additional 7 or 8 parameters required for the neutrino masses although neutrino masses are outside the standard model and the details are unclear). Research also focuses on the Hierarchy problem (why the weak scale and Planck scale are so disparate), and attempts to reconcile the emerging Standard Model of Cosmology with the Standard Model of particle physics. Many questions relate to the initial conditions that led to the presently observed Universe. Examples include: Why is there a matter/ antimatter asymmetry? Why is the Universe isotropic and homogeneous at large distances?

Retrieved from " http://en.wikipedia.org/w/index.php?title=Standard_Model&oldid=227771139"