Any measurement is subject to error by chance, meaning that if the measurement was taken again, it could possibly show a different value. We calculate the standard deviation in order to estimate the chance error for a single measurement. Taken further, we can calculate the chance error of the sample mean to estimate its accuracy in relation to the overall population mean.

Standard Error

In general terms, the standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate. For example, the sample mean is the standard estimator of a population mean. However, different samples drawn from that same population would, in general, have different values of the sample mean.

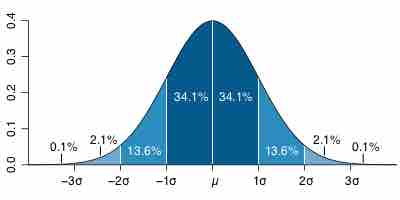
Standard Deviation as Standard Error

For a value that is sampled with an unbiased normally distributed error, the graph depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.

The standard error of the mean (i.e., standard error of using the sample mean as a method of estimating the population mean) is the standard deviation of those sample means over all possible samples (of a given size) drawn from the population. Secondly, the standard error of the mean can refer to an estimate of that standard deviation, computed from the sample of data being analyzed at the time.

In practical applications, the true value of the standard deviation (of the error) is usually unknown. As a result, the term standard error is often used to refer to an estimate of this unknown quantity. In such cases, it is important to clarify one's calculations, and take proper account of the fact that the standard error is only an estimate.

Standard Error of the Mean

As mentioned, the standard error of the mean (SEM) is the standard deviation of the sample-mean's estimate of a population mean. It can also be viewed as the standard deviation of the error in the sample mean relative to the true mean, since the sample mean is an unbiased estimator. Generally, the SEM is the sample estimate of the population standard deviation (sample standard deviation) divided by the square root of the sample size:

$\displaystyle S{ E }_{ \bar { x } }=\frac { s }{ \sqrt { n } }$

Where s is the sample standard deviation (i.e., the sample-based estimate of the standard deviation of the population), and $n$ is the size (number of observations) of the sample. This estimate may be compared with the formula for the true standard deviation of the sample mean:

$\displaystyle S{ D }_{ \bar { x } }=\frac { \sigma }{ \sqrt { n } }$

Where $\sigma$ is the standard deviation of the population. Note that the standard error and the standard deviation of small samples tend to systematically underestimate the population standard error and deviations because the standard error of the mean is a biased estimator of the population standard error. For example, with $n=2$, the underestimate is about 25%, but for $n=6$, the underestimate is only 5%. As a practical result, decreasing the uncertainty in a mean value estimate by a factor of two requires acquiring four times as many observations in the sample. Decreasing standard error by a factor of ten requires a hundred times as many observations.

Assumptions and Usage

If the data are assumed to be normally distributed, quantiles of the normal distribution and the sample mean and standard error can be used to calculate approximate confidence intervals for the mean. In particular, the standard error of a sample statistic (such as sample mean) is the estimated standard deviation of the error in the process by which it was generated. In other words, it is the standard deviation of the sampling distribution of the sample statistic.

Standard errors provide simple measures of uncertainty in a value and are often used for the following reasons:

• If the standard error of several individual quantities is known, then the standard error of some function of the quantities can be easily calculated in many cases.
• Where the probability distribution of the value is known, it can be used to calculate a good approximation to an exact confidence interval.
• Where the probability distribution is unknown, relationships of inequality can be used to calculate a conservative confidence interval.
• As the sample size tends to infinity, the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.