Overview
A wave is an oscillation that travels through space, accompanied by a transfer of energy. Wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass transport. They consist, instead, of oscillations or vibrations around almost fixed locations. There are two main types of waves. Mechanical waves propagate through a medium, and the substance of this medium is deformed. The deformation reverses itself owing to restoring forces resulting from its deformation.
The second main type of wave, electromagnetic waves, do not require a medium (although they may still propagate through a medium). Instead, they consist of periodic oscillations in electrical and magnetic fields generated by charged particles, and can therefore travel through a vacuum.
Wave Equation
The shape of a wave can take the form of any function that repeats itself over some characteristic spatial scale
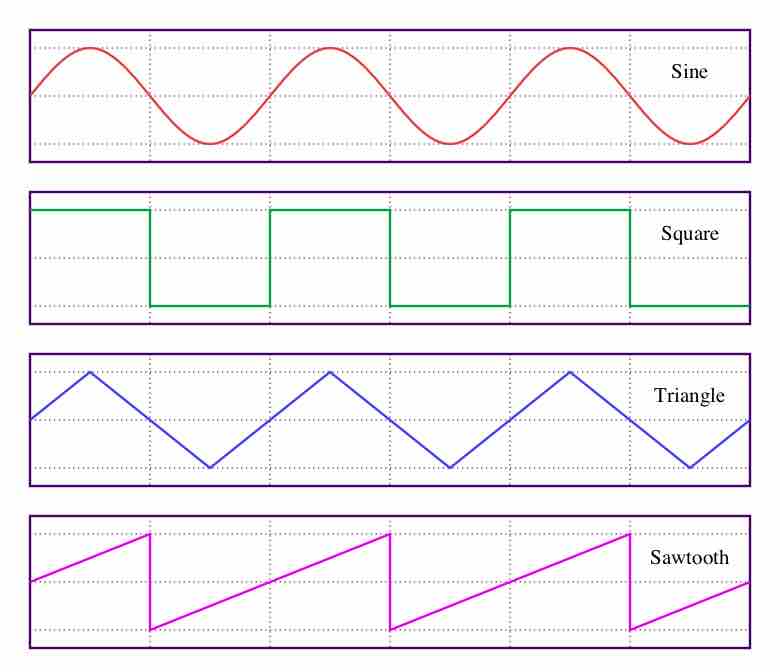
Common waveforms
A sample of several common, simple waveforms. A waveform is a function that repeats in space.
Sine Wave
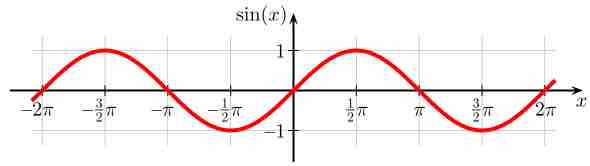
Plot of Sine
The sine function graphed on the Cartesian plane. In this graph, the angle x is given in radians (π = 180°).
Consider one of the most common waveforms, the sinusoid. A general form of a sinusoidal wave is
By taking derivatives, it is evident that the wave equation given above holds for
Arbitrary Wave
We looked closely into the sinusoidal wave. But how about waves that has a general form? One important aspect of the wave equation is its linearity: the wave equation is linear in u and it is left unaltered by translations in space and time. Since a wave with an arbitrary shape can be represented by a sum of many sinusoidal waves (this is called Fourier analysis), we can generate a great variety of solutions of the wave equation by translating and summing sine waves that we just looked closely into.