Forced Vibration and Resonance
Many people have played with toys involving an object supported by an elastic band: something like the paddle ball suspended from a finger in . Say a person drives the paddle ball by moving his or her finger up and down at a certain frequency. In this example, he or she is causing a forced oscillation (or vibration). At first the finger is held steady, and the ball bounces up and down with a small amount of damping. If the finger is moved up and down slowly, the ball will follow along without bouncing much on its own.
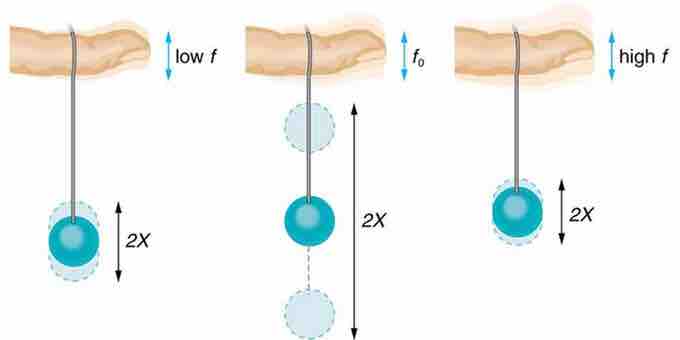
Paddle Balls and Frequencies
The paddle ball on its rubber band moves in response to the finger supporting it. If the finger moves with the natural frequency f0 of the ball on the rubber band, then a resonance is achieved, and the amplitude of the ball's oscillations increases dramatically. At higher and lower driving frequencies, energy is transferred to the ball less efficiently, and it responds with lower-amplitude oscillations.
As the frequency at which the finger is moved up and down increases, the ball will respond by oscillating with increasing amplitude. After driving the ball at its natural frequency, the ball's oscillations increase in amplitude with each oscillation for as long as it is driven. The phenomenon of driving a system with a frequency equal to its natural frequency is called resonance. As the driving frequency gets progressively higher than the resonant or natural frequency, the amplitude of the oscillations becomes smaller until the oscillations nearly disappear and the finger simply moves up and down with little effect on the ball.
Effects of Damping
In real life, most oscillators have damping present in the system. It is interesting that the widths of the resonance curves shown in depend on damping: the less the damping, the narrower the resonance. For a driven oscillator to resonate at a very specific frequency, there needs to be as little damping as possible, as is the case for piano strings and many other musical instruments. Conversely, for small-amplitude oscillations, such as in a car's suspension system, there needs to be heavy damping. Heavy damping reduces the amplitude, but the tradeoff is that the system responds at more frequencies.
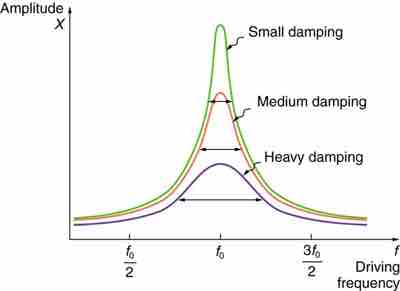
Damping
The amplitude of a harmonic oscillator is a function of the frequency of the driving force. The curves represent the same oscillator with the same natural frequency but with different amounts of damping. Resonance occurs when the driving frequency equals the natural frequency, and the greatest response is for the least amount of damping. The narrowest response is also for the least amount of damping.
Examples
These features of driven harmonic oscillators apply to a huge variety of systems. When tuning a radio, for example, people are adjusting the resonant frequency of the radio circuit so that it only oscillates to the desired station's broadcast (or driving) frequency. The more selective the radio is in discriminating between stations, the smaller its damping. A child on a swing is driven by a parent at the swing's natural frequency to achieve maximum amplitude. In all of these cases, the efficiency of energy transfer from the driving force into the oscillator is best at resonance. On gravel roads that are corrugated, if people travel at the 'wrong' speed, the bumps are very noticeable. At other speeds, it is difficult to feel the bumps at all. shows a photograph of a famous example (the Tacoma Narrows Bridge) of the destructive effects of a driven harmonic oscillation. Unfortunately, heavy winds happened to drive the bridge at its natural frequency, leading to the collapse.

Collapse of the Tacoma Narrows Bridge
In 1940, the Tacoma Narrows Bridge in Washington state collapsed. Heavy cross winds drove the bridge into oscillations at its resonant frequency. The damping decreased when support cables broke loose and started to slip over the towers, allowing increasingly greater amplitudes until the structure failed. (credit: PRI's Studio 360, via Flickr)