Standing Waves in Air Columns

Standing Waves

A standing wave is a wave that appears to be stationary, meaning it remains in a constant position. In an air column, a standing wave can form as either a longitudinal or transverse wave. A transverse wave, you may remember, is a wave where the movement of the particles of the medium is perpendicular to the direction of the propagation of the wave. A longitudinal wave, on the other hand, is parallel to the direction of propagation. A standing wave can occur when two identical waves moving in different directions interfere.

Air Columns

When a standing wave is formed in a tube, the standing wave has a maximum air displacement at the open end called an antinode. Here, the motion is unconstrained. At the closed end, there is no displacement; this is called a node, and the air is halted. The distance from a node to antinode is 1/4 of a wavelength, and is equal to the length of the tube.

shows that this resonance can be produced by a vibration introduced at or near the closed end of the tube as well. This is considered to be a natural vibration of the air column independently of how it is induced. Given that maximum air displacements are possible at the open end and none at the closed end, there are other, shorter wavelengths that can resonate in the tube. For example, a standing wave can have three-fourths of its wavelength in the tube, or L=(3/4)λ. This can be rendered as follows:

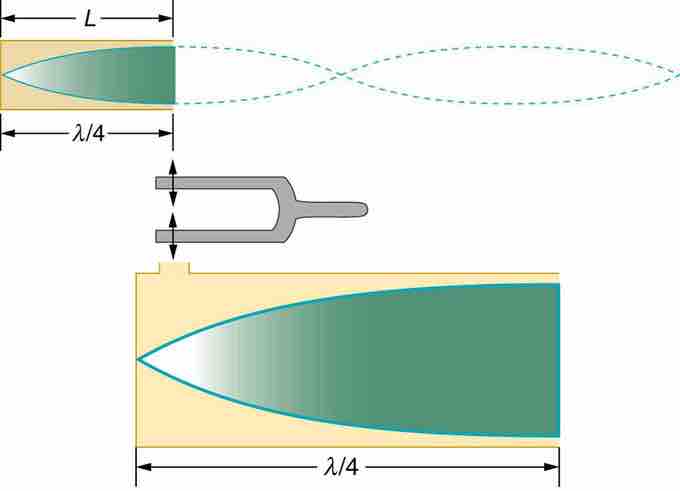
Standing Wave in Air Column

The same standing wave is created in the tube by a vibration introduced near its closed end.

$\lambda'=\frac{4L}3$

Continuing this process reveals a whole series of shorter-wavelength and higher-frequency sounds that resonate in the tube. We use specific terms for the resonances in any system. The lowest resonant frequency is called the fundamental, while all higher resonant frequencies are called overtones. All resonant frequencies are integral multiples of the fundamental, and they are collectively called harmonics. The fundamental is the first harmonic, the first overtone is the second harmonic, and so on. shows hows the fundamental and the first three overtones (the first four harmonics) in a tube closed at one end.

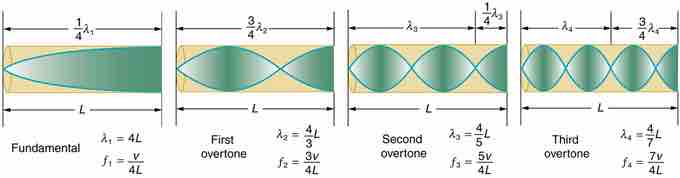
The First Four Harmonics

The fundamental and three lowest overtones for a tube closed at one end. All have maximum air displacements at the open end and none at the closed end.

Now let us look for a pattern in the resonant frequencies for a simple tube that is closed at one end. The fundamental has =4L, and frequency is related to wavelength and the speed of sound as given by the following:

$v_w=f\lambda $

Solving for f in this equation gives a more helpful form:

$f=\frac{v_w}\lambda =\frac{v_w}{4L}$

Here, f is frequency, v_w is speed of sound in air, λ is wavelength, and L is the length of the air column. The first overtone has = 4L/3. From this, we can deduce the following:

$f{'}=3\frac{v_w}{4L}=3f$

Because f′ = 3f, we call the first overtone the third harmonic. Continuing this process, we see a pattern that can be generalized in a single expression. The resonant frequencies of a tube closed at one end are:

$f_n=n\frac{vw}{4L} , n=1,3,5,$

Here, f1 is the fundamental, f3 is the first overtone, and so on. It is interesting that the resonant frequencies depend on the speed of sound and, hence, on temperature. This dependence poses a noticeable problem for organs in old unheated cathedrals, and it is also the reason why musicians commonly bring their wind instruments to room temperature before playing them.

Examples

The fundamental and overtones can be present simultaneously in a variety of combinations. For example, middle C on a trumpet has a sound distinctively different from middle C on a clarinet, both instruments being modified versions of a tube closed at one end. The fundamental frequency is the same (and usually the most intense), but the overtones and their mix of intensities are different and subject to shading by the musician. This mix is what gives various musical instruments (and human voices) their distinctive characteristics, whether they have air columns, strings, sounding boxes, or drumheads. In fact, much of our speech is determined by shaping the cavity formed by the throat and mouth and positioning the tongue to adjust the fundamental and combination of overtones. Simple resonant cavities can be made to resonate with the sound of the vowels, for example.