Pascal's Principle
Pascal's Principle (or Pascal's Law) applies to static fluids and takes advantage of the height dependency of pressure in static fluids. Named after French mathematician Blaise Pascal, who established this important relationship, Pascal's Principle can be used to exploit pressure of a static liquid as a measure of energy per unit volume to perform work in applications such as hydraulic presses. Qualitatively, Pascal's Principle states that pressure is transmitted undiminished in an enclosed static liquid. Quantitatively, Pascal's Law is derived from the expression for determining the pressure at a given height (or depth) within a fluid and is defined by Pascal's Principle:
where p1 is the external applied pressure, ρ is the density of the fluid, Δh is the difference in height of the static liquid, and g is the acceleration due to gravity. Pascal's Law explicitly determines the pressure difference between two different heights (or depths) within a static liquid. As, by Pascal's Law, a change in pressure is linearly proportional to a change in height within an incompressible, static liquid of constant density, doubling the height between the two points of reference will double the change of pressure, while halving the height between the two points will half the change in pressure.
Enclosed Static Liquids
While Pascal's Principle applies to any static fluid, it is most useful in terms of applications when considering systems involving rigid wall closed column configurations containing homogeneous fluids of constant density. By exploiting the fact that pressure is transmitted undiminished in an enclosed static liquid, such as in this type of system, static liquids can be used to transform small amounts of force into large amounts of force for many applications such as hydraulic presses.
As an example, referring to , a downwards force of 10 N is applied to a bottle filled with a static liquid of constant density ρ at the spout of cross-sectional area of 5 cm2, yielding an applied pressure of 2 N/cm2. The cross-sectional area of the bottle changes with height so that at the bottom of the bottle the cross-sectional area is 500 cm2. As a result of Pascal's Law, the pressure change (pressure applied to the static liquid) is transmitted undiminished in the static liquid so that the applied pressure is 2 N/m2 at the bottom of the bottle as well. Furthermore, the hydrostatic pressure due to the difference in height of the liquid is given by Equation 1 and yields the total pressure at the bottom surface of the bottle. Since the cross-sectional area at the bottom of the bottle is 100 times larger than at the top, the force contributing to the pressure at the bottom of the bottle is 1000 N plus the force from the weight of the static fluid in the bottle. This example shows how, through Pascal's Principle, the force exerted by a static fluid in a closed system can be multiplied by changing the height and the surface area of contact.

Pressure Applied to a Hydrostatic Fluid
A downwards force of 10 N is applied to a bottle filled with a static liquid of constant density ρ at the spout of cross-sectional area of 5 cm2, yielding an applied pressure of 2 N/cm2.
Pressure Transmitted Throughout an Entire Fluid
As stated by Pascal's Principle, the pressure applied to a static fluid in a closed container is transmitted throughout the entire fluid. Taking advantage of this phenomenon, hydraulic presses are able to exert a large amount of force requiring a much smaller amount of input force. gives two different types of hydraulic press configurations, the first in which there is no difference in height of the static liquid and the second in which there is a difference in height Δh of the static liquid. In the first configuration, a force F1 is applied to a static liquid of density ρ across a surface area of contact A1, yielding an input pressure of P2. On the other side of the press configuration, the fluid exerts an output pressure P1 across a surface area of contact A2, where A2 > A1. By Pascal's Principle, P1 = P2, yielding a force exerted by the static fluid of F2, where F2 > F1. Depending on the applied pressure and geometry of the hydraulic press, the magnitude of F2 can be changed. In the second configuration, the geometry of the system is the same, except that the height of the fluid on the output end is a height Δh less than the height of the fluid at the input end. The difference in height of the fluid between the input and the output ends contributes to the total force exerted by the fluid. For a hydraulic press, the force multiplication factor is the ratio of the output to the input contact areas.
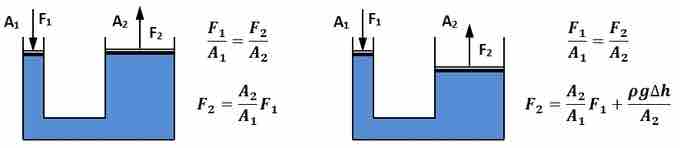
Hydraulic Press Diagrams
Two different types of hydraulic press configurations, the first in which there is no difference in height of the static liquid and the second in which there is a difference in height Δh of the static liquid.