Static equilibrium is a particular state of a physical system. It is qualitatively described by an object at rest and by the sum of all forces, with the sum of all torques acting on that object being equal to zero. Static objects are in static equilibrium, with the net force and net torque acting on that object being equal to zero; otherwise there would be a driving mechanism for that object to undergo movement in space. The analysis and study of objects in static equilibrium and the forces and torques acting on them is called statics—a subtopic of mechanics. Statics is particularly important in the design of static and load bearing structures. As it pertains to fluidics, static equilibrium concerns the forces acting on a static object within a fluid medium.
Fluids
For a fluid at rest, the conditions for static equilibrium must be met at any point within the fluid medium. Therefore, the sum of the forces and torques at any point within the static liquid or gas must be zero. Similarly, the sum of the forces and torques of an object at rest within a static fluid medium must also be zero. In considering a stationary object within a liquid medium at rest, the forces acting at any point in time and at any point in space within the medium must be analyzed. For a stationary object within a static liquid, there are no torques acting on the object so the sum of the torques for such a system is immediately zero; it need not concern analysis since the torque condition for equilibrium is fulfilled.
Density
At any point in space within a static fluid, the sum of the acting forces must be zero; otherwise the condition for static equilibrium would not be met. In analyzing such a simple system, consider a rectangular region within the fluid medium with density ρL (same density as the fluid medium), width w, length l, and height h, as shown in . Next, the forces acting on this region within the medium are taken into account. First, the region has a force of gravity acting downwards (its weight) equal to its density object, times its volume of the object, times the acceleration due to gravity. The downward force acting on this region due to the fluid above the region is equal to the pressure times the area of contact. Similarly, there is an upward force acting on this region due to the fluid below the region equal to the pressure times the area of contact. For static equilibrium to be achieved, the sum of these forces must be zero, as shown in . Thus for any region within a fluid, in order to achieve static equilibrium, the pressure from the fluid below the region must be greater than the pressure from the fluid above by the weight of the region. This force which counteracts the weight of a region or object within a static fluid is called the buoyant force (or buoyancy).

Static Equilibrium of a Region Within a Fluid
This figure shows the equations for static equilibrium of a region within a fluid.
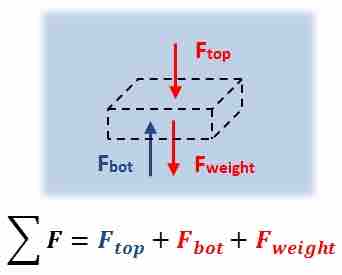
Region Within a Static Fluid
This figure is a free body diagram of a region within a static fluid.
In the case on an object at stationary equilibrium within a static fluid, the sum of the forces acting on that object must be zero. As previously discussed, there are two downward acting forces, one being the weight of the object and the other being the force exerted by the pressure from the fluid above the object. At the same time, there is an upwards force exerted by the pressure from the fluid below the object, which includes the buoyant force. shows how the calculation of the forces acting on a stationary object within a static fluid would change from those presented in if an object having a density ρS different from that of the fluid medium is surrounded by the fluid. The appearance of a buoyant force in static fluids is due to the fact that pressure within the fluid changes as depth changes. The analysis presented above can furthermore be extended to much more complicated systems involving complex objects and diverse materials.