Section 5
Vector Calculus
By Boundless

A vector field is an assignment of a vector to each point in a subset of Euclidean space.
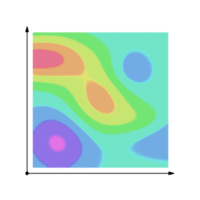
A conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential.
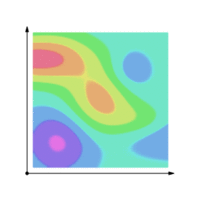
A line integral is an integral where the function to be integrated is evaluated along a curve.
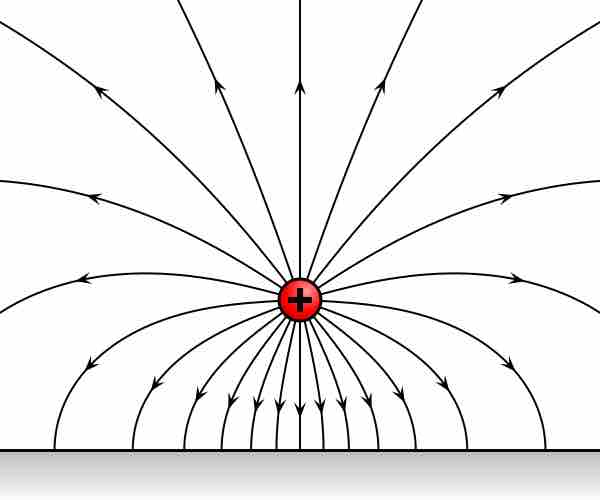
Gradient theorem says that a line integral through a gradient field can be evaluated from the field values at the endpoints of the curve.
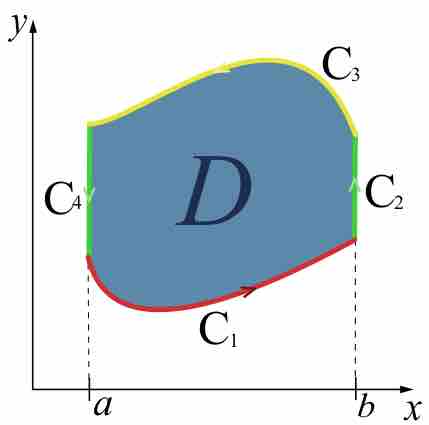
Green's theorem gives relationship between a line integral around closed curve

The four most important differential operators are gradient, curl, divergence, and Laplacian.
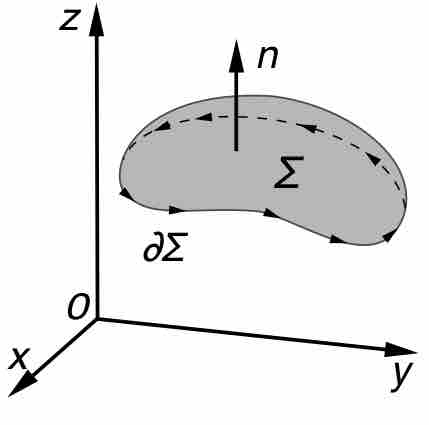
A parametric surface is a surface in the Euclidean space
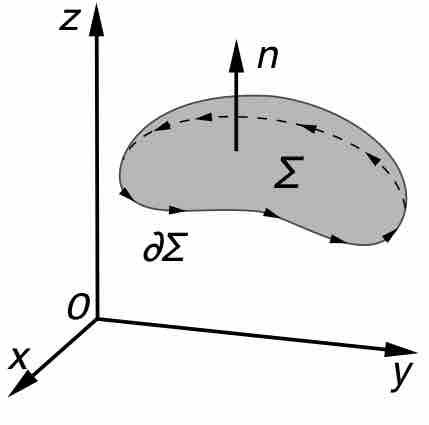
The surface integral of vector fields can be defined component-wise according to the definition of the surface integral of a scalar field.
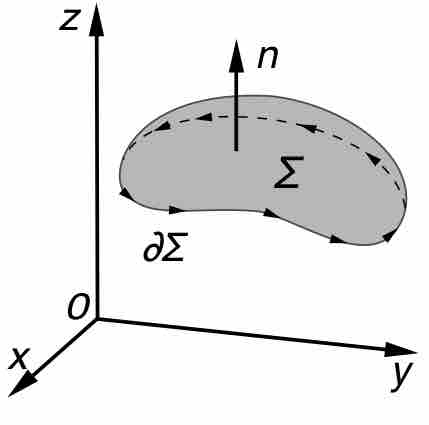
Stokes' theorem relates the integral of the curl of a vector field over a surface to the line integral of the field around the boundary.
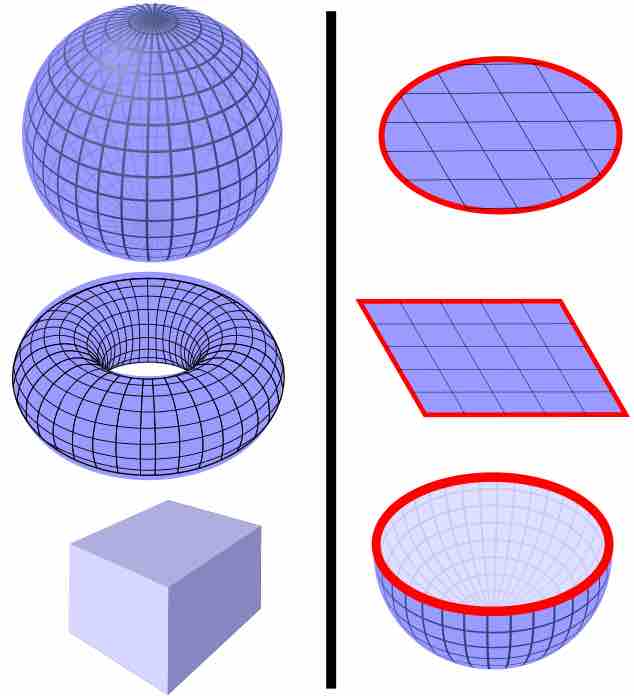
The divergence theorem relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.