Conservative Vector Fields

A conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential. Conservative vector fields have the following property: The line integral from one point to another is independent of the choice of path connecting the two points; it is path-independent. 

Conversely, path independence is equivalent to the vector field's being conservative. Conservative vector fields are also irrotational, meaning that (in three dimensions) they have vanishing curl. In fact, an irrotational vector field is necessarily conservative provided that a certain condition on the geometry of the domain holds: it must be simply connected.

Definition: A vector field $\mathbf{v}$ is said to be conservative if there exists a scalar field $\varphi$ such that $\mathbf{v}=\nabla\varphi$. Here $\nabla\varphi$ denotes the gradient of $\varphi$. When the above equation holds, $\varphi$ is called a scalar potential for $\mathbf{v}$.

For any scalar field $\varphi$: $\nabla \times \nabla \varphi=0$. Therefore, the curl of a conservative vector field $\mathbf{v}$ is always $0$. A vector field $\mathbf{v}$, whose curl is zero, is called irrotational .

Fig 1

The above field $\mathbf{v}(x,y,z) = (\frac{−y}{x^2+y^2}, \frac{x}{x^2+y^2}, 0)$ includes a vortex at its center, meaning it is non-irrotational; it is neither conservative, nor does it have path independence. However, any simply connected subset that excludes the vortex line $(0,0,z)$ will have zero curl, $\nabla \mathbf{v}=0$. Such vortex-free regions are examples of irrotational vector fields.

Path Independence

A key property of a conservative vector field is that its integral along a path depends only on the endpoints of that path, not the particular route taken. Suppose that $S\subseteq\mathbb{R}^3$is a region of three-dimensional space, and that $P$ is a rectifiable path in $S$ with start point $A$ and end point $B$. If $\mathbf{v}=\nabla\varphi$ is a conservative vector field, then the gradient theorem states that $\int_P \mathbf{v}\cdot d\mathbf{r}=\varphi(B)-\varphi(A)$. This holds as a consequence of the Chain Rule and the Fundamental Theorem of Calculus. An equivalent formulation of this is to say that $\oint \mathbf{v}\cdot d\mathbf{r}=0$ for every closed loop in $S$.

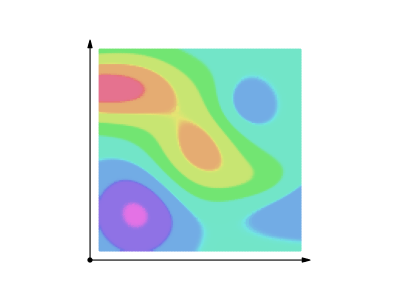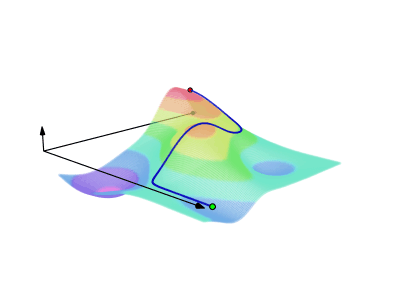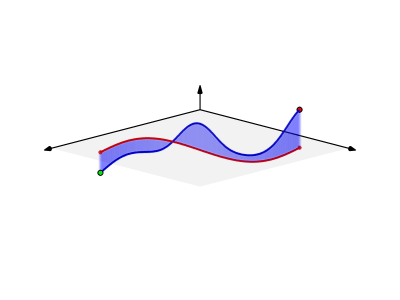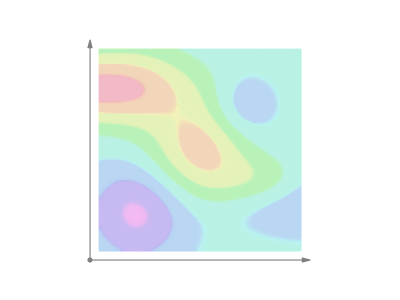
Line Integral Over Scalar Field

The line integral over a scalar field $f$ can be thought of as the area under the curve $C$ along a surface $z=f(x,y)$, described by the field.