Parametric Surface
A parametric surface is a surface in the Euclidean space
Examples
- The simplest type of parametric surfaces is given by the graphs of functions of two variables:
$z=f(x,y)$ ;$\vec{r}(x,y)=(x,y,f(x,y))$ . - Using the spherical coordinates, the unit sphere can be parameterized by
$\vec r(\theta,\phi) = (\cos\theta \sin\phi, \sin\theta \sin \phi, \cos\phi), 0 \leq \theta < 2\pi, 0 \leq \phi \leq \pi$ . - The straight circular cylinder of radius
$R$ about the$x$ -axis has the following parametric representation:$\vec{r}(x,\phi)=(x,R \cos \phi, r \sin \phi)$ .
The same surface admits many different parametrizations. For example, the coordinate
Surface integral
A surface integral is a definite integral taken over a surface . It can be thought of as the double integral analog of the line integral. Given a surface, one may integrate over its scalar fields (that is, functions which return scalars as values), and vector fields (that is, functions which return vectors as values). Surface integrals have many applications in physics, particularly within the classical theory of electromagnetism. We will study surface integral of vector fields and related theorems in the following atoms.
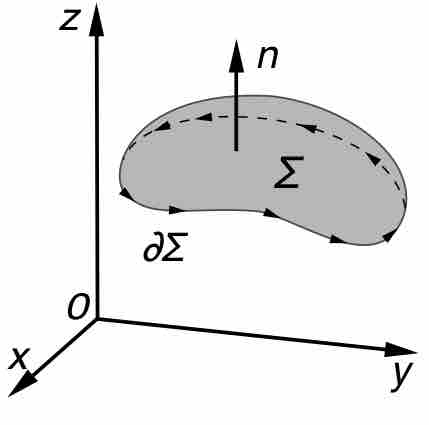
Kelvin-Stokes' Theorem
An illustration of the Kelvin–Stokes theorem, with surface