A line integral (sometimes called a path integral, contour integral, or curve integral) is an integral where the function to be integrated is evaluated along a curve.
The function to be integrated may be a scalar field or a vector field. The value of the line integral is the sum of the values of the field at all points on the curve, weighted by some scalar function on the curve (commonly arc length or, for a vector field, the scalar product of the vector field with a differential vector in the curve). This weighting distinguishes the line integral from simpler integrals defined on intervals. Many simple formulae in physics (for example,
In qualitative terms, a line integral in vector calculus can be thought of as a measure of the total effect of a given field along a given curve. More specifically, the line integral over a scalar field can be interpreted as the area under the field carved out by a particular curve. This can be visualized as the surface created by
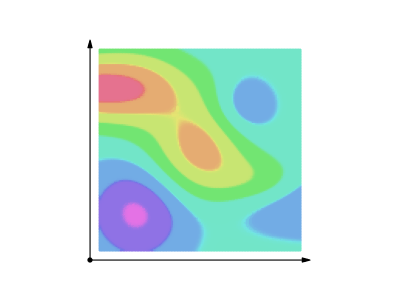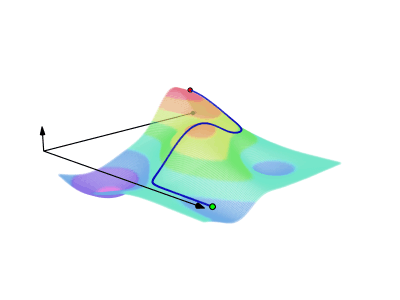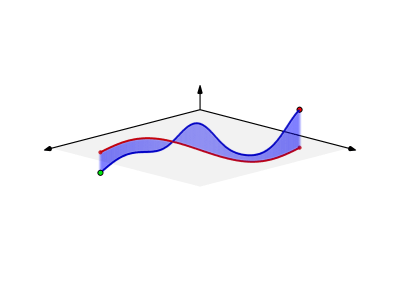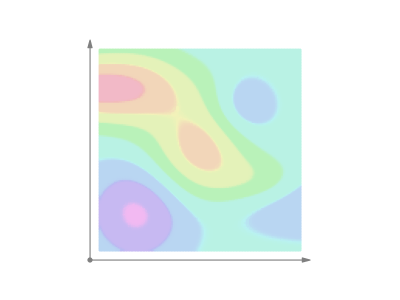
Line Integral Over Scalar Field
The line integral over a scalar field
Line Integral of a Scalar Field
For some scalar field
where
Line Integral of a Vector Field
For a vector field
where