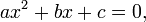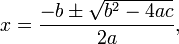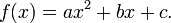Portal:Algebra
Algebra
Algebra is a branch of mathematics concerning the study of structure, relation and quantity. The name is derived from the treatise written by the Persian mathematician, astronomer, astrologer and geographer, Muhammad bin Mūsā al-Khwārizmī titled Kitab al-Jabr al-Muqabala (meaning " The Compendious Book on Calculation by Completion and Balancing"), which provided operations for the systematic solution of linear and quadratic equation
Together with geometry, analysis, combinatorics, and number theory, algebra is one of the main branches of mathematics. Elementary algebra is often part of the curriculum in secondary education and provides an introduction to the basic ideas of algebra, including effects of adding and multiplying numbers, the concept of variables, definition of polynomials, along with factorization and determining their roots.
In addition to working directly with numbers, algebra covers working with symbols, variables, and set elements. Addition and multiplication are viewed as general operations, and their precise definitions lead to structures such as groups, rings and fields.
Selected article
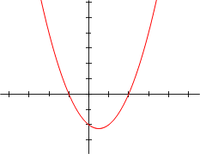
| The graph of a real-valued quadratic function of a real variable x, is a parabola. |
A quadratic equation is a polynomial equation of degree two. The general form is
where a ≠ 0 (if a = 0, then the equation becomes a linear equation). The letters a, b, and c are called coefficients: the quadratic coefficient a is the coefficient of x2, the linear coefficient b is the coefficient of x, and c is the constant coefficient, also called the free term.
Quadratic equations are called quadratic because quadratus is Latin for "square"; in the leading term the variable is squared.
A quadratic equation has two (not necessarily distinct) solutions, which may be real or complex, given by the quadratic formula:
These solutions are roots of the corresponding quadratic function
| Image credit: Enoch Lau |
Did you know?
- ...that it is impossible to devise a single formula involving only polynomials and radicals for solving an arbitrary quintic equation?
- ...that it is possible for a three dimensional figure to have a finite volume but infinite surface area? An example of this is Gabriel's Horn.
- ...that the Gudermannian function relates the regular trigonometric functions and the hyperbolic trigonometric functions without the use of complex numbers?
- ...that the classification of finite simple groups was not completed until the mid 1980s?
- ...that a field is an algebraic structure in which the operations of addition, subtraction, multiplication and division (except division by zero) may be performed, and the same rules hold which are familiar from the arithmetic of ordinary numbers?