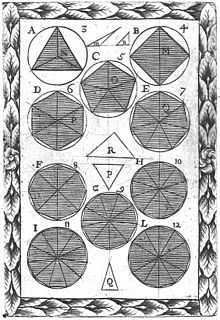
Polygon
Background Information
This selection is made for schools by a children's charity read more. All children available for child sponsorship from SOS Children are looked after in a family home by the charity. Read more...
In geometry a polygon (pron.: / ˈ p ɒ l ɪ ɡ ɒ n /) is a flat shape consisting of straight lines that are joined to form a closed chain or circuit.
A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments (i.e., by a closed polygonal chain). These segments are called its edges or sides, and the points where two edges meet are the polygon's vertices (singular: vertex) or corners. An n-gon is a polygon with n sides. The interior of the polygon is sometimes called its body. A polygon is a 2-dimensional example of the more general polytope in any number of dimensions.
The word "polygon" derives from the Greek πολύς (polús) "much", "many" and γωνία (gōnía) "corner", "angle", or γόνυ (gónu) "knee".
The basic geometrical notion has been adapted in various ways to suit particular purposes. Mathematicians are often concerned only with the closed polygonal chain and with simple polygons which do not self-intersect, and may define a polygon accordingly. Geometrically two edges meeting at a corner are required to form an angle that is not straight (180°); otherwise, the line segments will be considered parts of a single edge; however mathematically, such corners may sometimes be allowed. In fields relating to computation, the term polygon has taken on a slightly altered meaning derived from the way the shape is stored and manipulated in computer graphics (image generation). Some other generalizations of polygons are described below.
Classification
Number of sides
Polygons are primarily classified by the number of sides. See table below.
Convexity and types of non-convexity
Polygons may be characterized by their convexity or type of non-convexity:
- Convex: any line drawn through the polygon (and not tangent to an edge or corner) meets its boundary exactly twice. Equivalently, all its interior angles are less than 180°.
- Non-convex: a line may be found which meets its boundary more than twice. In other words, it contains at least one interior angle with a measure larger than 180°.
- Simple: the boundary of the polygon does not cross itself. All convex polygons are simple.
- Concave: Non-convex and simple.
- Star-shaped: the whole interior is visible from a single point, without crossing any edge. The polygon must be simple, and may be convex or concave.
- Self-intersecting: the boundary of the polygon crosses itself. Branko Grünbaum calls these coptic, though this term does not seem to be widely used. The term complex is sometimes used in contrast to simple, but this usage risks confusion with the idea of a complex polygon as one which exists in the complex Hilbert plane consisting of two complex dimensions.
- Star polygon: a polygon which self-intersects in a regular way.
Symmetry
- Equiangular: all its corner angles are equal.
- Cyclic: all corners lie on a single circle.
- Isogonal or vertex-transitive: all corners lie within the same symmetry orbit. The polygon is also cyclic and equiangular.
- Equilateral: all edges are of the same length. (A polygon with 5 or more sides can be equilateral without being convex.)
- Isotoxal or edge-transitive: all sides lie within the same symmetry orbit. The polygon is also equilateral.
- Tangential: all sides are tangent to an inscribed circle.
- Regular: A polygon is regular if it is both cyclic and equilateral. A non-convex regular polygon is called a regular star polygon.
Properties
Euclidean geometry is assumed throughout.
Angles
Any polygon, regular or irregular, self-intersecting or simple, has as many corners as it has sides. Each corner has several angles. The two most important ones are:
- Interior angle – The sum of the interior angles of a simple n-gon is (n − 2)π radians or (n − 2)180 degrees. This is because any simple n-gon can be considered to be made up of (n − 2) triangles, each of which has an angle sum of π radians or 180 degrees. The measure of any interior angle of a convex regular n-gon is
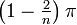 radians or
radians or 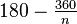 degrees. The interior angles of regular star polygons were first studied by Poinsot, in the same paper in which he describes the four regular star polyhedra.
degrees. The interior angles of regular star polygons were first studied by Poinsot, in the same paper in which he describes the four regular star polyhedra.
- Exterior angle – Tracing around a convex n-gon, the angle "turned" at a corner is the exterior or external angle. Tracing all the way around the polygon makes one full turn, so the sum of the exterior angles must be 360°. This argument can be generalized to concave simple polygons, if external angles that turn in the opposite direction are subtracted from the total turned. Tracing around an n-gon in general, the sum of the exterior angles (the total amount one rotates at the vertices) can be any integer multiple d of 360°, e.g. 720° for a pentagram and 0° for an angular "eight", where d is the density or starriness of the polygon. See also orbit (dynamics).
The exterior angle is the supplementary angle to the interior angle. From this the sum of the interior angles can be easily confirmed, even if some interior angles are more than 180°: going clockwise around, it means that one sometime turns left instead of right, which is counted as turning a negative amount. (Thus we consider something like the winding number of the orientation of the sides, where at every vertex the contribution is between −1⁄2 and 1⁄2 winding.)
Area and centroid
The area of a polygon is the measurement of the 2-dimensional region enclosed by the polygon. For a non-self-intersecting ( simple) polygon with n vertices, the area and centroid are given by:
To close the polygon, the first and last vertices are the same, i.e., xn, yn = x0, y0. The vertices must be ordered according to positive or negative orientation (counterclockwise or clockwise, respectively); if they are ordered negatively, the value given by the area formula will be negative but correct in absolute value, but when calculating 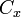 and
and 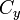 , the signed value of
, the signed value of 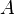 (which in this case is negative) should be used. This is commonly called the Surveyor's Formula.
(which in this case is negative) should be used. This is commonly called the Surveyor's Formula.
The area formula is derived by taking each edge AB, and calculating the (signed) area of triangle ABO with a vertex at the origin O, by taking the cross-product (which gives the area of a parallelogram) and dividing by 2. As one wraps around the polygon, these triangles with positive and negative area will overlap, and the areas between the origin and the polygon will be cancelled out and sum to 0, while only the area inside the reference triangle remains. This is why the formula is called the Surveyor's Formula, since the "surveyor" is at the origin; if going counterclockwise, positive area is added when going from left to right and negative area is added when going from right to left, from the perspective of the origin.
The formula was described by Meister in 1769 and by Gauss in 1795. It can be verified by dividing the polygon into triangles, but it can also be seen as a special case of Green's theorem.
The area A of a simple polygon can also be computed if the lengths of the sides, a1, a2, ..., an and the exterior angles, θ1, θ2, ..., θn are known. The formula is
The formula was described by Lopshits in 1963.
If the polygon can be drawn on an equally spaced grid such that all its vertices are grid points, Pick's theorem gives a simple formula for the polygon's area based on the numbers of interior and boundary grid points.
In every polygon with perimeter p and area A , the isoperimetric inequality 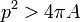 holds.
holds.
If any two simple polygons of equal area are given, then the first can be cut into polygonal pieces which can be reassembled to form the second polygon. This is the Bolyai-Gerwien theorem.
The area of a regular polygon is also given in terms of the radius r of its inscribed circle and its perimeter p by
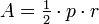 .
.
This radius is also termed its apothem and is often represented as a.
The area of a regular n-gon with side s inscribed in a unit circle is
 .
.
The area of a regular n-gon in terms of the radius r of its circumscribed circle and its perimeter p is given by
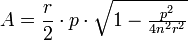 .
.
The area of a regular n-gon, inscribed in a unit-radius circle, with side s and interior angle θ can also be expressed trigonometrically as
 .
.
The sides of a polygon do not in general determine the area. However, if the polygon is cyclic the sides do determine the area. Of all n-gons with given sides, the one with the largest area is cyclic. Of all n-gons with a given perimeter, the one with the largest area is regular (and therefore cyclic).
Self-intersecting polygons
The area of a self-intersecting polygon can be defined in two different ways, each of which gives a different answer:
- Using the above methods for simple polygons, we discover that particular regions within the polygon may have their area multiplied by a factor which we call the density of the region. For example the central convex pentagon in the centre of a pentagram has density 2. The two triangular regions of a cross-quadrilateral (like a figure 8) have opposite-signed densities, and adding their areas together can give a total area of zero for the whole figure.
- Considering the enclosed regions as point sets, we can find the area of the enclosed point set. This corresponds to the area of the plane covered by the polygon, or to the area of a simple polygon having the same outline as the self-intersecting one (or, in the case of the cross-quadrilateral, the two simple triangles).
Degrees of freedom
An n-gon has 2n degrees of freedom, including 2 for position, 1 for rotational orientation, and 1 for overall size, so 2n − 4 for shape. In the case of a line of symmetry the latter reduces to n − 2.
Let k ≥ 2. For an nk-gon with k-fold rotational symmetry (Ck), there are 2n − 2 degrees of freedom for the shape. With additional mirror-image symmetry (Dk) there are n − 1 degrees of freedom.
Product of distances from a vertex to other vertices of a regular polygon
For a regular n-gon inscribed in a unit-radius circle, the product of the distances from a given vertex to all other vertices equals n.
Generalizations of polygons
In a broad sense, a polygon is an unbounded (without ends) sequence or circuit of alternating segments (sides) and angles (corners). An ordinary polygon is unbounded because the sequence closes back in itself in a loop or circuit, while an apeirogon (infinite polygon) is unbounded because it goes on forever. The modern mathematical understanding is to describe such a structural sequence in terms of an " abstract" polygon which is a partially ordered set (poset) of elements. The interior (body) of the polygon is another element, and (for technical reasons) so is the null polytope or nullitope.
A geometric polygon is a realization of the associated abstract polygon. This involves some mapping of elements from the abstract to the geometric. Such a polygon does not have to lie in a plane, or have straight sides, or enclose an area, and individual elements can overlap or even coincide. For example a spherical polygon is drawn on the surface of a sphere, and its sides are arcs of great circles.
A digon is a closed polygon having two sides and two corners. Two opposing points on a spherical surface, joined by two different half great circles produce a digon. Tiling the sphere with digons produces a polyhedron called a hosohedron. One great circle with one corner point added, produces a monogon or henagon.
Other realizations of these polygons are possible on other surfaces, but in the Euclidean (flat) plane, their bodies cannot be sensibly realized and are considered degenerate.
The idea of a polygon has been generalized in various ways. A short list of some degenerate cases (or special cases) comprises the following:
- Digon: Interior angle of 0° in the Euclidean plane. See remarks above regarding the sphere
- Interior angle of 180°: In the plane this gives an apeirogon (see below), on the sphere a dihedron
- A skew polygon does not lie in a flat plane, but zigzags in three (or more) dimensions. The Petrie polygons of the regular polyhedra are classic examples
- A spherical polygon is a circuit of sides and corners on the surface of a sphere
- An apeirogon is an infinite sequence of sides and angles, which is not closed but it has no ends because it extends infinitely
- A complex polygon is a figure analogous to an ordinary polygon, which exists in the complex Hilbert plane
Naming polygons
The word "polygon" comes from Late Latin polygōnum (a noun), from Greek πολύγωνον (polygōnon/polugōnon), noun use of neuter of πολύγωνος (polygōnos/polugōnos, the masculine adjective), meaning "many-angled". Individual polygons are named (and sometimes classified) according to the number of sides, combining a Greek-derived numerical prefix with the suffix -gon, e.g. pentagon, dodecagon. The triangle, quadrilateral or quadrangle, and nonagon are exceptions. For large numbers, mathematicians usually write the numeral itself, e.g. 17-gon. A variable can even be used, usually n-gon. This is useful if the number of sides is used in a formula.
Some special polygons also have their own names; for example the regular star pentagon is also known as the pentagram.
| Name | Edges | Remarks |
|---|---|---|
| henagon (or monogon) | 1 | In the Euclidean plane, degenerates to a closed curve with a single vertex point on it. |
| digon | 2 | In the Euclidean plane, degenerates to a closed curve with two vertex points on it. |
| triangle (or trigon) | 3 | The simplest polygon which can exist in the Euclidean plane. |
| quadrilateral (or quadrangle or tetragon) | 4 | The simplest polygon which can cross itself; the simplest polygon which can be concave. |
| pentagon | 5 | The simplest polygon which can exist as a regular star. A star pentagon is known as a pentagram or pentacle. |
| hexagon | 6 | Avoid "sexagon" = Latin [sex-] + Greek. |
| heptagon | 7 | Avoid "septagon" = Latin [sept-] + Greek. The simplest polygon such that the regular form is not constructible with compass and straightedge. However, it can be constructed using a Neusis construction. |
| octagon | 8 | |
| enneagon or nonagon | 9 | "Nonagon" is commonly used but mixes Latin [novem = 9] with Greek. Some modern authors prefer "enneagon", which is pure Greek. |
| decagon | 10 | |
| hendecagon | 11 | Avoid "undecagon" = Latin [un-] + Greek. The simplest polygon such that the regular form cannot be constructed with compass, straightedge, and angle trisector. |
| dodecagon | 12 | Avoid "duodecagon" = Latin [duo-] + Greek. |
| tridecagon (or triskaidecagon) | 13 | |
| tetradecagon (or tetrakaidecagon) | 14 | |
| pentadecagon (or quindecagon or pentakaidecagon) | 15 | |
| hexadecagon (or hexakaidecagon) | 16 | |
| heptadecagon (or heptakaidecagon) | 17 | |
| octadecagon (or octakaidecagon) | 18 | |
| enneadecagon (or enneakaidecagon or nonadecagon) | 19 | |
| icosagon | 20 | |
| triacontagon | 30 | |
| hectogon | 100 | "hectogon" is the Greek name (see hectometer), "centagon" is a Latin-Greek hybrid; neither is widely attested. |
| chiliagon | 1000 | René Descartes, Immanuel Kant, David Hume, and others have used the chiliagon as an example in philosophical discussion. |
| myriagon | 10,000 | |
| megagon | 1,000,000 | As with René Descartes' example of the chiliagon, the million-sided polygon has been used as an illustration of a well-defined concept that cannot be visualised. The megagon is also used as an illustration of the convergence of regular polygons to a circle. |
| apeirogon |  |
A degenerate polygon of infinitely many sides |
Constructing higher names
To construct the name of a polygon with more than 20 and less than 100 edges, combine the prefixes as follows
| Tens | and | Ones | final suffix | ||
|---|---|---|---|---|---|
| -kai- | 1 | -hena- | -gon | ||
| 20 | icosa- | 2 | -di- | ||
| 30 | triaconta- | 3 | -tri- | ||
| 40 | tetraconta- | 4 | -tetra- | ||
| 50 | pentaconta- | 5 | -penta- | ||
| 60 | hexaconta- | 6 | -hexa- | ||
| 70 | heptaconta- | 7 | -hepta- | ||
| 80 | octaconta- | 8 | -octa- | ||
| 90 | enneaconta- | 9 | -ennea- | ||
The "kai" is not always used. Opinions differ on exactly when it should, or need not, be used (see also examples above).
Alternatively, the system used for naming the higher alkanes (completely saturated hydrocarbons) can be used:
| Ones | Tens | final suffix | ||
|---|---|---|---|---|
| 1 | hen- | 10 | deca- | -gon |
| 2 | do- | 20 | -cosa- | |
| 3 | tri- | 30 | triaconta- | |
| 4 | tetra- | 40 | tetraconta- | |
| 5 | penta- | 50 | pentaconta- | |
| 6 | hexa- | 60 | hexaconta- | |
| 7 | hepta- | 70 | heptaconta- | |
| 8 | octa- | 80 | octaconta- | |
| 9 | ennea- (or nona-) | 90 | enneaconta- (or nonaconta-) | |
This has the advantage of being consistent with the system used for 10- through 19-sided figures.
That is, a 42-sided figure would be named as follows:
| Ones | Tens | final suffix | full polygon name |
|---|---|---|---|
| do- | tetraconta- | -gon | dotetracontagon |
and a 50-sided figure
| Tens | and | Ones | final suffix | full polygon name |
|---|---|---|---|---|
| pentaconta- | -gon | pentacontagon | ||
But beyond enneagons and decagons, professional mathematicians generally prefer the aforementioned numeral notation (for example, MathWorld has articles on 17-gons and 257-gons). Exceptions exist for side counts that are more easily expressed in verbal form.
History
Polygons have been known since ancient times. The regular polygons were known to the ancient Greeks, and the pentagram, a non-convex regular polygon ( star polygon), appears on the vase of Aristophonus, Caere, dated to the 7th century B.C. Non-convex polygons in general were not systematically studied until the 14th century by Thomas Bradwardine.
In 1952, Geoffrey Colin Shephard generalized the idea of polygons to the complex plane, where each real dimension is accompanied by an imaginary one, to create complex polygons.
Polygons in nature
Numerous regular polygons may be seen in nature. In the world of geology, crystals have flat faces, or facets, which are polygons. Quasicrystals can even have regular pentagons as faces. Another fascinating example of regular polygons occurs when the cooling of lava forms areas of tightly packed hexagonal columns of basalt, which may be seen at the Giant's Causeway in Ireland, or at the Devil's Postpile in California.
The most famous hexagons in nature are found in the animal kingdom. The wax honeycomb made by bees is an array of hexagons used to store honey and pollen, and as a secure place for the larvae to grow. There also exist animals who themselves take the approximate form of regular polygons, or at least have the same symmetry. For example, sea stars display the symmetry of a pentagon or, less frequently, the heptagon or other polygons. Other echinoderms, such as sea urchins, sometimes display similar symmetries. Though echinoderms do not exhibit exact radial symmetry, jellyfish and comb jellies do, usually fourfold or eightfold.
Radial symmetry (and other symmetry) is also widely observed in the plant kingdom, particularly amongst flowers, and (to a lesser extent) seeds and fruit, the most common form of such symmetry being pentagonal. A particularly striking example is the starfruit, a slightly tangy fruit popular in Southeast Asia, whose cross-section is shaped like a pentagonal star.
Moving off the earth into space, early mathematicians doing calculations using Newton's law of gravitation discovered that if two bodies (such as the sun and the earth) are orbiting one another, there exist certain points in space, called Lagrangian points, where a smaller body (such as an asteroid or a space station) will remain in a stable orbit. The sun-earth system has five Lagrangian points. The two most stable are exactly 60 degrees ahead and behind the earth in its orbit; that is, joining the centre of the sun and the earth and one of these stable Lagrangian points forms an equilateral triangle. Astronomers have already found asteroids at these points. It is still debated whether it is practical to keep a space station at the Lagrangian point – although it would never need course corrections, it would have to frequently dodge the asteroids that are already present there. There are already satellites and space observatories at the less stable Lagrangian points.
Polygons in computer graphics
A polygon in a computer graphics (image generation) system is a two-dimensional shape that is modelled and stored within its database. A polygon can be colored, shaded and textured, and its position in the database is defined by the coordinates of its vertices (corners).
Naming conventions differ from those of mathematicians:
- A simple polygon does not cross itself.
- a concave polygon is a simple polygon having at least one interior angle greater than 180°.
- A complex polygon does cross itself.
Use of Polygons in Real-time imagery: The imaging system calls up the structure of polygons needed for the scene to be created from the database. This is transferred to active memory and finally, to the display system (screen, TV monitors etc.) so that the scene can be viewed. During this process, the imaging system renders polygons in correct perspective ready for transmission of the processed data to the display system. Although polygons are two dimensional, through the system computer they are placed in a visual scene in the correct three-dimensional orientation so that as the viewing point moves through the scene, it is perceived in 3D.
Morphing: To avoid artificial effects at polygon boundaries where the planes of contiguous polygons are at different angle, so called "Morphing Algorithms" are used. These blend, soften or smooth the polygon edges so that the scene looks less artificial and more like the real world.
Meshed Polygons: The number of meshed polygons ("meshed" is like a fish net) can be up to twice that of free-standing unmeshed polygons, particularly if the polygons are contiguous. If a square mesh has n + 1 points (vertices) per side, there are n squared squares in the mesh, or 2n squared triangles since there are two triangles in a square. There are (n + 1)2 / 2(n2) vertices per triangle. Where n is large, this approaches one half. Or, each vertex inside the square mesh connects four edges (lines).
Polygon Count: Since a polygon can have many sides and need many points to define it, in order to compare one imaging system with another, "polygon count" is generally taken as a triangle. When analyzing the characteristics of a particular imaging system, the exact definition of polygon count should be obtained as it applies to that system as there is some flexibility in processing which causes comparisons to become non-trivial.
Vertex Count: Although using this metric appears to be closer to reality it still must be taken with some salt. Since each vertex can be augmented with other attributes (such as colour or normal) the amount of processing involved cannot be trivially inferred. Furthermore, the applied vertex transform is to be accounted, as well topology information specific to the system being evaluated as post-transform caching can introduce consistent variations in the expected results.
Point in polygon test: In computer graphics and computational geometry, it is often necessary to determine whether a given point P = (x0,y0) lies inside a simple polygon given by a sequence of line segments. It is known as the Point in polygon test.



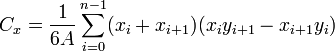
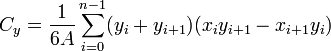
![\begin{align}A = \frac12 ( a_1[a_2 \sin(\theta_1) + a_3 \sin(\theta_1 + \theta_2) + \cdots + a_{n-1} \sin(\theta_1 + \theta_2 + \cdots + \theta_{n-2})] \\
{} + a_2[a_3 \sin(\theta_2) + a_4 \sin(\theta_2 + \theta_3) + \cdots + a_{n-1} \sin(\theta_2 + \cdots + \theta_{n-2})] \\
{} + \cdots + a_{n-2}[a_{n-1} \sin(\theta_{n-2})] ) \end{align}](../../images/2168/216877.png)