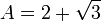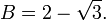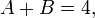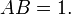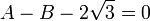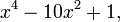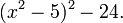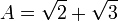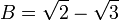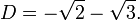Galois theory
Background to the schools Wikipedia
This Wikipedia selection is available offline from SOS Children for distribution in the developing world. Click here for more information on SOS Children.
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory. Using Galois theory, certain problems in field theory can be reduced to group theory, which is in some sense simpler and better understood.
Originally Galois used permutation groups to describe how the various roots of a given polynomial equation are related to each other. The modern approach to Galois theory, developed by Richard Dedekind, Leopold Kronecker and Emil Artin, among others, involves studying automorphisms of field extensions.
Further abstraction of Galois theory is achieved by the theory of Galois connections.
Application to classical problems
The birth of Galois theory was originally motivated by the following question, whose answer is known as the Abel–Ruffini theorem.
- "Why is there no formula for the roots of a fifth (or higher) degree polynomial equation in terms of the coefficients of the polynomial, using only the usual algebraic operations (addition, subtraction, multiplication, division) and application of radicals (square roots, cube roots, etc)?"
Galois theory not only provides a beautiful answer to this question, it also explains in detail why it is possible to solve equations of degree four or lower in the above manner, and why their solutions take the form that they do. Further, it gives a conceptually clear, and often practical, means of telling when some particular equation of higher degree can be solved in that manner.
Galois theory also gives a clear insight into questions concerning problems in compass and straightedge construction. It gives an elegant characterisation of the ratios of lengths that can be constructed with this method. Using this, it becomes relatively easy to answer such classical problems of geometry as
- "Which regular polygons are constructible polygons?"
- "Why is it not possible to trisect every angle?"
History
Galois theory originated in the study of symmetric functions – the coefficients of a polynomial are (up to sign) the elementary symmetric polynomials in the roots. For instance, (x – a)(x – b) = x2 – (a + b)x + ab, where 1, a + b and ab are the elementary polynomials of degree 0, 1 and 2 in two variables.
This was first formalized by the 16th century French mathematician François Viète, in Viète's formulas, for the case of positive real roots. In the opinion of the 18th century British mathematician Charles Hutton, the expression of coefficients of a polynomial in terms of the roots (not only for positive roots) was first understood by the 17th century French mathematician Albert Girard; Hutton writes:
...[Girard was] the first person who understood the general doctrine of the formation of the coefficients of the powers from the sum of the roots and their products. He was the first who discovered the rules for summing the powers of the roots of any equation.
In this vein, the discriminant is a symmetric function in the roots which reflects properties of the roots – it is zero if and only if the polynomial has a multiple root, and for quadratic and cubic polynomials it is positive if and only if all roots are real and distinct, and negative if and only if there is a pair of distinct complex conjugate roots. See Discriminant: nature of the roots for details.
The cubic was first partly solved by the 15th/16th century Italian mathematician Scipione del Ferro, who did not however publish his results; this method only solved one of three classes, as the others involved taking square roots of negative numbers, and complex numbers were not known at the time. This solution was then rediscovered independently in 1535 by Niccolò Fontana Tartaglia, who shared it with Gerolamo Cardano, asking him to not publish it. Cardano then extended this to the other two cases, using square roots of negatives as intermediate steps; see details at Cardano's method. After the discovery of Ferro's work, he felt that Tartaglia's method was no longer secret, and thus he published his complete solution in his 1545 Ars Magna. His student Lodovico Ferrari solved the quartic polynomial, which solution Cardano also included in Ars Magna.
A further step was the 1770 paper Réflexions sur la résolution algébrique des équations by the French-Italian mathematician Joseph Louis Lagrange, in his method of Lagrange resolvents, where he analyzed Cardano and Ferrarri's solution of cubics and quartics by considering them in terms of permutations of the roots, which yielded an auxiliary polynomial of lower degree, providing a unified understanding of the solutions and laying the groundwork for group theory and Galois theory. Crucially, however, he did not consider composition of permutations. Lagrange's method did not extend to quintic equations or higher, because the resolvent had higher degree.
The quintic was almost proven to have no general solutions by radicals by Paolo Ruffini in 1799, whose key insight was to use permutation groups, not just a single permutation. His solution contained a gap, which Cauchy considered minor, though this was not patched until the work of Norwegian mathematician Niels Henrik Abel, who published a proof in 1824, thus establishing the Abel–Ruffini theorem.
While Ruffini and Abel established that the general quintic could not be solved, some particular quintics can be solved, such as (x − 1)5, and the precise criterion by which a given quintic or higher polynomial could be determined to be solvable or not was given by Évariste Galois, who showed that whether a polynomial was solvable or not was equivalent to whether or not the permutation group of its roots – in modern terms, its Galois group – had a certain structure – in modern terms, whether or not it was a solvable group. This group was always solvable for polynomials of degree four or less, but not always so for polynomials of degree five and greater, which explains why there is no general solution in higher degree.
The permutation group approach to Galois theory
Given a polynomial, it may be that some of the roots are connected by various algebraic equations. For example, it may be that for two of the roots, say A and B, that A2 + 5B3 = 7. The central idea of Galois theory is to consider those permutations (or rearrangements) of the roots having the property that any algebraic equation satisfied by the roots is still satisfied after the roots have been permuted. An important proviso is that we restrict ourselves to algebraic equations whose coefficients are rational numbers. (One might instead specify a certain field in which the coefficients should lie but, for the simple examples below, we will restrict ourselves to the field of rational numbers.)
These permutations together form a permutation group, also called the Galois group of the polynomial (over the rational numbers). To illustrate this point, consider the following examples:
First example — a quadratic equation
Consider the quadratic equation
By using the quadratic formula, we find that the two roots are
Examples of algebraic equations satisfied by A and B include
and
Obviously, in either of these equations, if we exchange A and B, we obtain another true statement. For example, the equation A + B = 4 becomes simply B + A = 4. Furthermore, it is true, but far less obvious, that this holds for every possible algebraic equation with rational coefficients satisfied by the roots A and B; to prove this requires the theory of symmetric polynomials.
We conclude that the Galois group of the polynomial x2 − 4x + 1 consists of two permutations: the identity permutation which leaves A and B untouched, and the transposition permutation which exchanges A and B. It is a cyclic group of order two, and therefore isomorphic to Z/2Z.
One might object that A and B are related by yet another algebraic equation,
which does not remain true when A and B are exchanged. However, this equation does not concern us, because it does not have rational coefficients; in particular,  is not rational.
is not rational.
A similar discussion applies to any quadratic polynomial ax2 + bx + c, where a, b and c are rational numbers.
- If the polynomial has only one root, for example x2 − 4x + 4 = (x−2)2, then the Galois group is trivial; that is, it contains only the identity permutation.
- If it has two distinct rational roots, for example x2 − 3x + 2 = (x−2)(x−1), the Galois group is again trivial.
- If it has two irrational roots (including the case where the roots are complex), then the Galois group contains two permutations, just as in the above example.
Second example
Consider the polynomial
which can also be written as
We wish to describe the Galois group of this polynomial, again over the field of rational numbers. The polynomial has four roots:
There are 24 possible ways to permute these four roots, but not all of these permutations are members of the Galois group. The members of the Galois group must preserve any algebraic equation with rational coefficients involving A, B, C and D. One such equation is
- A + D = 0.
However, since
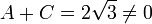 ,
,
the permutation
- (A, B, C, D) → (A, B, D, C)
is not permitted (because it transforms the valid equation A + D = 0 into the invalid equation A + C = 0).
Another equation that the roots satisfy is
This will exclude further permutations, such as
- (A, B, C, D) → (A, C, B, D).
Continuing in this way, we find that the only permutations (satisfying both equations simultaneously) remaining are
- (A, B, C, D) → (A, B, C, D)
- (A, B, C, D) → (C, D, A, B)
- (A, B, C, D) → (B, A, D, C)
- (A, B, C, D) → (D, C, B, A),
and the Galois group is isomorphic to the Klein four-group.
The modern approach by field theory
In the modern approach, one starts with a field extension L/K (read: L over K), and examines the group of field automorphisms of L/K (these are mappings α: L → L with α(x) = x for all x in K). See the article on Galois groups for further explanation and examples.
The connection between the two approaches is as follows. The coefficients of the polynomial in question should be chosen from the base field K. The top field L should be the field obtained by adjoining the roots of the polynomial in question to the base field. Any permutation of the roots which respects algebraic equations as described above gives rise to an automorphism of L/K, and vice versa.
In the first example above, we were studying the extension Q(√3)/Q, where Q is the field of rational numbers, and Q(√3) is the field obtained from Q by adjoining √3. In the second example, we were studying the extension Q(A,B,C,D)/Q.
There are several advantages to the modern approach over the permutation group approach.
- It permits a far simpler statement of the fundamental theorem of Galois theory.
- The use of base fields other than Q is crucial in many areas of mathematics. For example, in algebraic number theory, one often does Galois theory using number fields, finite fields or local fields as the base field.
- It allows one to more easily study infinite extensions. Again this is important in algebraic number theory, where for example one often discusses the absolute Galois group of Q, defined to be the Galois group of K/Q where K is an algebraic closure of Q.
- It allows for consideration of inseparable extensions. This issue does not arise in the classical framework, since it was always implicitly assumed that arithmetic took place in characteristic zero, but nonzero characteristic arises frequently in number theory and in algebraic geometry.
- It removes the rather artificial reliance on chasing roots of polynomials. That is, different polynomials may yield the same extension fields, and the modern approach recognizes the connection between these polynomials.
Solvable groups and solution by radicals
The notion of a solvable group in group theory allows one to determine whether a polynomial is solvable in the radicals, depending on whether its Galois group has the property of solvability. In essence, each field extension L/K corresponds to a factor group in a composition series of the Galois group. If a factor group in the composition series is cyclic of order n, then if the corresponding field extension is an extension of a field containing a primitive root of unity, then it is a radical extension, and the elements of L can then be expressed using the nth root of some element of K.
If all the factor groups in its composition series are cyclic, the Galois group is called solvable, and all of the elements of the corresponding field can be found by repeatedly taking roots, products, and sums of elements from the base field (usually Q).
One of the great triumphs of Galois Theory was the proof that for every n > 4, there exist polynomials of degree n which are not solvable by radicals—the Abel–Ruffini theorem. This is due to the fact that for n > 4 the symmetric group Sn contains a simple, non-cyclic, normal subgroup.
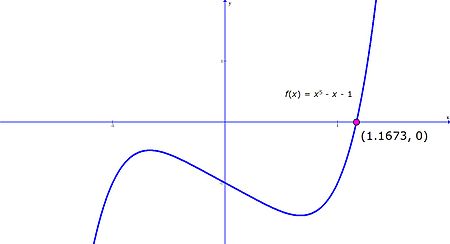
 . The lone real root
. The lone real root 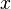 =1.1673... is algebraic, but not expressible as radicals. The other four roots are complex numbers.
=1.1673... is algebraic, but not expressible as radicals. The other four roots are complex numbers.A non-solvable quintic example
Van der Waerden cites the polynomial  . By the rational root theorem it has no rational zeros. Neither does it have linear factors modulo 2 or 3.
. By the rational root theorem it has no rational zeros. Neither does it have linear factors modulo 2 or 3.
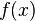 has the factorization
has the factorization  modulo 2. That means its Galois group modulo 2 is cyclic of order 6.
modulo 2. That means its Galois group modulo 2 is cyclic of order 6.
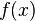 has no quadratic factor modulo 3. Thus its Galois group modulo 3 has order 5.
has no quadratic factor modulo 3. Thus its Galois group modulo 3 has order 5.
We know that a Galois group modulo a prime is isomorphic to a subgroup of the Galois group over the rationals. A permutation group on 5 objects with operations of orders 6 and 5 must be the symmetric group 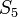 , which must be the Galois group of
, which must be the Galois group of 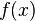 . This is one of the simplest examples of a non-solvable quintic polynomial. Serge Lang said that Artin was fond of this example.
. This is one of the simplest examples of a non-solvable quintic polynomial. Serge Lang said that Artin was fond of this example.
The inverse Galois problem
All finite groups do occur as Galois groups. It is easy to construct field extensions with any given finite group as Galois group, as long as one does not also specify the ground field.
For that, choose a field K and a finite group G. Cayley's theorem says that G is (up to isomorphism) a subgroup of the symmetric group S on the elements of G. Choose indeterminates {xα}, one for each element α of G, and adjoin them to K to get the field F = K({xα}). Contained within F is the field L of symmetric rational functions in the {xα}. The Galois group of F/L is S, by a basic result of Emil Artin. G acts on F by restriction of action of S. If the fixed field of this action is M, then, by the fundamental theorem of Galois theory, the Galois group of F/M is G.
It is an open problem to prove the existence of a field extension of the rational field Q with a given finite group as Galois group. Hilbert played a part in solving the problem for all symmetric and alternating groups. Igor Shafarevich proved that every solvable finite group is the Galois group of some extension of Q. Various people have solved the inverse Galois problem for selected non-abelian simple groups. Existence of solutions has been shown for all but possibly one ( Mathieu group M23) of the 26 sporadic simple groups. There is even a polynomial with integral coefficients whose Galois group is the Monster group.