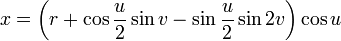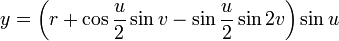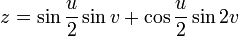File:KleinBottle-Figure8-01.png

KleinBottle-Figure8-01.png ‎(560 × 400 pixels, file size: 149 KB, MIME type: image/png)

This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help.

Summary

Description

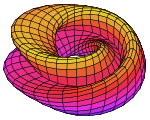
Figure-eight immersion of a Klein bottle into R³. Made with Mathematica.

English: The "figure 8" immersion of the Klein bottle.

Italiano: L'immersione a "figura 8" della bottiglia di Klein.

Русский: Реализация бутылки Клейна в виде восьмерки

Date

05/08/06

Source

Own drawing, Mathematica 5.1

Author

Fropuff, Inductiveload

Permission
( Reusing this file)

The original image was released into the public domain by Fropuff:

This work has been released into the public domain by its author, Fropuff. This applies worldwide.
In some countries this may not be legally possible; if so:
Fropuff grants anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.

Public domainPublic domainfalsefalse

The derived, redrawn, edited image was released into the public domain by Inductiveload:

This work has been released into the public domain by its author, Inductiveload. This applies worldwide.
In some countries this may not be legally possible; if so:
Inductiveload grants anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.

Public domainPublic domainfalsefalse

File:KleinBottle-Figure8-01.svg is a vector version of this file.
It should be used in place of this raster image when superior.

File:KleinBottle-Figure8-01.png

File:KleinBottle-Figure8-01.svg

For more information about vector graphics, read about Commons transition to SVG.
There is also information about MediaWiki's support of SVG images.

Parameterization

This immersion of the Klein bottle into R³ is given by the following parameterization. Here the parameters u and v run from 0 to 2π and r is some fixed positive constant.

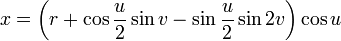
$x = \left(r + \cos\frac{u}{2}\sin v - \sin\frac{u}{2}\sin 2v\right) \cos u$

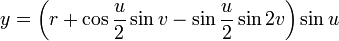
$y = \left(r + \cos\frac{u}{2}\sin v - \sin\frac{u}{2}\sin 2v\right) \sin u$

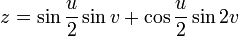
$z = \sin\frac{u}{2}\sin v + \cos\frac{u}{2}\sin 2v$

Mathematica source

Klein8[r_:2] =
 Function[{u, v},
   {
       (r + Cos[u/2]Sin[v] - Sin[u/2]Sin[2v]) Cos[u],
       (r + Cos[u/2]Sin[v] - Sin[u/2]Sin[2v]) Sin[u],
       Sin[u/2]Sin[v] + Cos[u/2]Sin[2v]
   }
 ]

 ParametricPlot3D[Evaluate[Klein8[][u, v]], {u, 0, 2Pi}, {v, 0, 2Pi},
   PlotPoints -> 60, Boxed -> False, Axes -> False, ImageSize -> 800]

This image was then antialised with Chris Hill's code, made transparent around the surface and had stray pixels removed in an image editor.

File usage

The following pages on Schools Wikipedia link to this image (list may be incomplete):

Klein bottle

What is Schools Wikipedia?

Schools Wikipedia was created by children's charity SOS Children's Villages. SOS Children believes education is an important part of a child's life. That's why we ensure they receive nursery care as well as high-quality primary and secondary education. When they leave school, we support the children in our care as they progress to vocational training or higher education. There are many ways to help with SOS Childrens Villages.