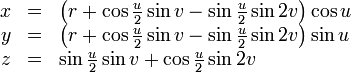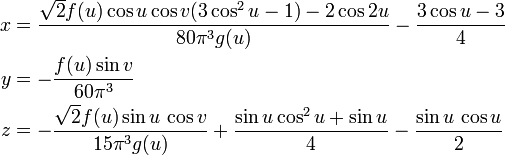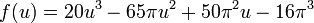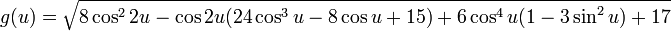Klein bottle
Background Information
SOS Children offer a complete download of this selection for schools for use on schools intranets. All children available for child sponsorship from SOS Children are looked after in a family home by the charity. Read more...
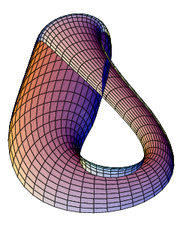
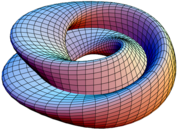
In mathematics, the Klein bottle is a certain non- orientable surface, i.e., a surface (a two-dimensional topological space) with no distinct "inner" and "outer" sides. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a two dimensional object with one side and one edge, a Klein bottle is a three dimensional object with one side and no edges. (For comparison, a sphere is a three dimensional object with no edges and two sides.)
The Klein bottle was first described in 1882 by the German mathematician Felix Klein. It was originally named the Kleinsche Fläche "Klein surface"; however, this was incorrectly interpreted as Kleinsche Flasche "Klein bottle", which ultimately led to the adoption of this term in the German language as well.
Construction
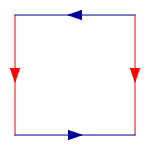
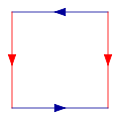
Start with a square, and then glue together corresponding colored edges, in the following diagram, so that the arrows match. More formally, the Klein bottle is the quotient space described as the square [0,1] × [0,1] with sides identified by the relations (0,y) ~ (1, y) for 0 ≤ y ≤ 1 and (x, 0) ~ (1 − x, 1) for 0 ≤ x ≤ 1:
This square is a fundamental polygon of the Klein bottle.
Note that this is an "abstract" gluing in the sense that trying to realize this in three dimensions results in a self-intersecting Klein bottle. The Klein bottle, proper, does not self-intersect. Nonetheless, there is a way to visualize the Klein bottle as being contained in four dimensions.
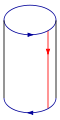
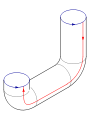
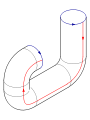
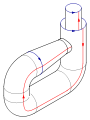
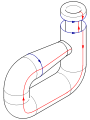
Glue the red arrows of the square together (left and right sides), resulting in a cylinder. To glue the ends together so that the arrows on the circles match, pass one end through the side of the cylinder. Note that this creates a circle of self-intersection. This is an immersion of the Klein bottle in three dimensions.
By adding a fourth dimension to the three dimensional space, the self-intersection can be eliminated. Gradually push a piece of the tube containing the intersection out of the original three dimensional space. A useful analogy is to consider a self-intersecting curve on the plane; self-intersections can be eliminated by lifting one strand off the plane.
This immersion is useful for visualizing many properties of the Klein bottle. For example, the Klein bottle has no boundary, where the surface stops abruptly, and it is non-orientable, as reflected in the one-sidedness of the immersion.
The common physical model of a Klein bottle is a similar construction. The British Science Museum has on display a collection of hand-blown glass Klein bottles, exhibiting many variations on this topological theme. The bottles date from 1995 and were made for the museum by Alan Bennett. Clifford Stoll, author of The Cuckoo's Egg, manufactures Klein bottles and sells them via the Internet at Acme Klein Bottle.
Properties
The Klein bottle can be seen as a fibre bundle as follows: one takes the square from above to be E, the total space, while the base space B is given by the unit interval in x, and the projection π is given by π(x, y) = x. Since the two endpoints of the unit interval in x are identified, the base space B is actually the circle S1, and so the Klein bottle is the twisted S1-bundle ( circle bundle) over the circle.
Like the Möbius strip, the Klein bottle is a two-dimensional differentiable manifold which is not orientable. Unlike the Möbius strip, the Klein bottle is a closed manifold, meaning it is a compact manifold without boundary. While the Möbius strip can be embedded in three-dimensional Euclidean space R3, the Klein bottle cannot. It can be embedded in R4, however.
The Klein bottle can be constructed (in a mathematical sense, because it cannot be done without allowing the surface to intersect itself) by joining the edges of two Möbius strips together, as described in the following anonymous limerick:
- A mathematician named Klein
- Thought the Möbius band was divine.
- Said he: "If you glue
- The edges of two,
- You'll get a weird bottle like mine."
It can also be constructed by folding a Möbius strip in half lengthwise and attaching the edge to itself.
Six colors suffice to colour any map on the surface of a Klein bottle; this is the only exception to the Heawood conjecture, a generalization of the four colour theorem, which would require seven.
A Klein bottle is equivalent to a sphere plus two cross caps.
Dissection
Dissecting a Klein bottle into halves along its plane of symmetry results in two mirror image Möbius strips, i.e. one with a left-handed half-twist and the other with a right-handed half-twist (one of these is pictured on the right). Remember that the intersection pictured isn't really there. In fact, it is also possible to cut the Klein bottle into a single Möbius strip.
Parametrization
The "figure 8" immersion of the Klein bottle has a particularly simple parametrization:
In this immersion, the self-intersection circle is a geometric circle in the xy plane. The positive constant r is the radius of this circle. The parameter u gives the angle in the xy plane, and v specifies the position around the 8-shaped cross section.
The parametrization of the 3-dimensional immersion of the bottle itself is much more complicated. Here is a simplified version:
where
for 0 ≤ u < 2π and 0 ≤ v < 2π.
In this parametrization, u follows the length of the bottle's body while v goes around its circumference.
Generalizations
The generalization of the Klein bottle to higher genus is given in the article on the fundamental polygon.
Klein surface
A Klein surface is, as for Riemann surfaces, a surface with an atlas allowing that the transition functions can be composed with complex conjugation one can obtains the so called dianalytic structure.